2519
Through-plane Motion in Magnetic Resonance Fingerprinting: Simulations and Phantom Experiments1Imaging Physics, Delft University of Technology, Delft, Netherlands, 2Institute for Biomedical Enginering, ETH Zurich, Zurich, Switzerland, 3Philips Research Europe, Hamburg, Germany
Synopsis
-
Introduction
Motion correction for MR Fingerprinting1 has been applied mostly to (rigid) in-plane motion2. A general intrinsic robustness of MRF to through-plane motion has been observed3, however, the authors also note that simply excluding motion-effected intervals from MRF matching yield strong bias, especially in T2, depending on the temporal distribution of the motion pattern.Therefore, in this study a method is proposed to simulate through-plane motion effects in Extended Phase Graph(EPG) simulations for MRF with the goal of improving parameter estimation in cases of such motion by matching against a motion-augmented dictionary.
Methods
Simulations
A slice profile-corrected EPG algorithm4,5 was implemented as illustrated in Fig. 1. Slice profiles were obtained using the hard-pulse approximation. To simulate through-plane motion, the EPG-states were moved in the slice direction(z-direction) by a discrete number of steps before each RF-pulse. This enables the simulation of arbitrary motion patterns across time. Simulations were performed with a single T1 and T2-combination, assuming homogeneity in the z-direction.Dictionaries for different motion patterns (see last row in Fig. 5) were calculated for values of T1 = 200 − 1800ms, T2 = 30−500ms(5% steps) and $$$B_1^+=90\%-110\%$$$(1%-point steps). The RF-shape was discretized in 400 steps. Calculations were performed in Python with Numba-JIT compiling to reduce computation time6. Simulations on a standard desktop PC took approximately 12s per dictionary atom.
Acquisitions
MRF acquisitions were performed on a 3T Philips Achieva MRI (Philips, Best, The Netherlands). Sequence input files were adapted to include an extra parameter to adjust slice positioning for each RF pulse during the sequence separately. A spoiled-SSFP MRF-sequence was used7. All scans were performed on the EuroSpin phantom (see Fig.2 for reference T1, T2 maps), such that movement took place along the direction of the vials, guaranteeing that equal T1 and T2 was entering and leaving the slice. All scans were preceded by an adiabatic, non slice-selective inversion pulse. The following scans were performed:- Fully-sampled Cartesian acquisition, sequence length 500 (interpolated version of Fig. 1)8
(a) Without motion;
(b) Step-like motion at index no. 250. - Undersampled constant-density spiral acquisition (sampling: 1/32), sequence length 1000 (see Fig.1 for Flip angle pattern and see Fig.4 for motion patterns)
(a) Without motion;
(b) Step-like motion at index no. 500;
(c) Sinusoidal motion with maximum relative amplitude of 80%;(d) Smooth, random-like motion with maximum relative amplitude of 80%.
Dictionary matching was performed on the measured data with corrected and uncorrected dictionaries. $$$B_1^+$$$ estimates were obtained by matching Cartesian motion data (1b) to the complete dictionary. $$$B_1^+$$$ was fixed in the remaining matches.
Results and Discussion
Comparison between simulation and fully sampled Cartesian measurements (Fig.3a-b) shows that the effects of through-plane motion can be simulated accurately. Motion leads to strong signal variations, caused by unperturbed longitudinal magnetization entering the slice.We observed that $$$B_1^+$$$-effects show a strong influence on the effect of sudden motion (see Fig.3c), resulting in a $$$B_1^+$$$-dependent phase drift in the transient oscillations.
Correction to motion effects could be applied effectively for fully sampled data (see Fig.4) and T2-errors were minimized. In undersampled spiral acquisitions motion resulted in a T2-overestimation(Fig. 5), as has been observed before in literature. Errors were more pronounced for longer T2-times (see Fig.2 for comparison). This T2-error was decreased for sinusoidal and random-like motion by matching with a corrected dictionary. Correction for step-like motion resulted in an increased, spatially heterogeneous error in both T1 and T2. We hypothesize that this is caused by the sudden peak in signal and interplay with undersampling artifacts9, possibly reduced by the use of improved reconstruction methods10, with an SVD-compression from the corrected dictionary.
The motion simulation makes the simplifying assumption that only the F0 configuration state is leading to signal (spoiling condition). However, motion also leads to spatial asymmetries in the magnetization response (Fig.1), allowing higher-order states to contribute to the signal. This may lead to additional off-resonance dependency of the signal, which was not accounted for here11.
A limitation of the proposed work is the assumption that the same T1,T2-properties leave and enter the slice. However T2-errors as introduced by motion are often larger than the differences between neighboring tissues, making this simplification justifiable.
Here, we restricted the analysis to motion on the order of the slice thickness. However, motion in freebreathing abdominal imaging can be multiples thereof. One approach is the use of prospective slice-tracking. Our results can be viewed as add-on motion correction accounting for residual relative motion.
In our experiments, the motion pattern was known beforehand, which is in reality not the case. However, estimation of through-plane motion, e.g. through correlation with the signal from a respiratory bellow or camera-based tracking system may be possible allowing to augment the dictionary after the scan.
Conclusion
We have shown a method to include through-plane motion into the EPG simulation that leads to improved T2 results when matching against a motion-augmented MRF dictionary in the absence of additional undersampling effects.Acknowledgements
This work was partly funded by the Medical Delta consortium. The authors want to thank Kay Nehrke, Gastoa Cruz for fruitful discussion and Peter Koken for supplying the base MR Fingerprinting patch. This work originated from the 3rd MR Fingerprinting Workshop at Philips Research Hamburg.References
(1) Ma, D.; Gulani, V.; Seiberlich, N.; Liu, K.; Sunshine, J. L.; Duerk, J. L.; Griswold, M. A. Nature 2013, 495, 187–192, DOI: 10.1038/nature11971.
(2) Cruz, G.; Jaubert, O.; Schneider, T.; Botnar, R. M.; Prieto, C. Magnetic Resonance in Medicine 2019, 81, 947–961, DOI: 10.1002/mrm.27448.
(3) Yu, Z.; Zhao, T.; Assl¨ander, J.; Lattanzi, R.; Sodickson, D. K.; Cloos, M. A. Magnetic Resonance Imaging 2018, 54, 241–248, DOI: 10.1016/j.mri.2018.09.002.
(4) Hennig, J. Concepts in Magnetic Resonance 1991, 3, 125–143, DOI: 10.1002/cmr.1820030302.
(5) Malik, S. J.; Padormo, F.; Price, A. N.; Hajnal, J. V. Magnetic Resonance in Medicine 2012, 68, 1481–1494, DOI: 10.1002/mrm.24153.
(6) Lam, S. K.; Pitrou, A.; Seibert, S. In Proceedings of the Second Workshop on the LLVM Compiler Infrastructure in HPC, Association for Computing Machinery: New York, NY, USA, 2015, pp 1–6, DOI: 10.1145/2833157.2833162.
(7) Jiang, Y.; Ma, D.; Seiberlich, N.; Gulani, V.; Griswold, M. A. Magnetic Resonance in Medicine 2015, 74, 1621–1631, DOI: 10.1002/mrm.25559.
(8) Sommer, K.; Amthor, T.; Doneva, M.; Koken, P.; Meineke, J.; B¨ornert, P. Magnetic Resonance Imaging 2017, 41, 7–14, DOI: 10.1016/j.mri.2017.06.015.
(9) Stolk, C. C.; Sbrizzi, A. IEEE Transactions on Medical Imaging 2019, 1–1, DOI: 10.1109/TMI.2019. 2900585.
(10) Asslander, J.; Cloos, M. A.; Knoll, F.; Sodickson, D. K.; Hennig, J.; Lattanzi, R. Magnetic Resonance in Medicine 2018, 79, 83–96, DOI: 10.1002/mrm.26639.
(11) Guenthner, C.; Amthor, T.; Doneva, M.; Kozerke, S. Scientific Reports 2021, 11, 1–19, DOI: 10.1038/ s41598-021-00233-6.
Figures
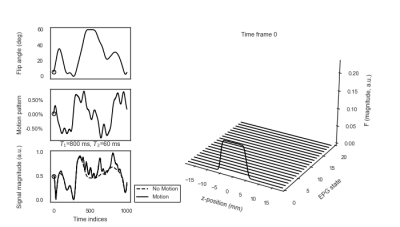
Figure 1 (Animation): Left: MRF flip angle train of length 1000 (top) with a prescribed motion pattern in z-direction (middle) and its effect on a single signal trajectory (bottom). Right: EPG state at varying time points.
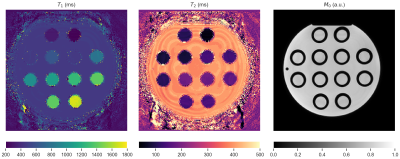
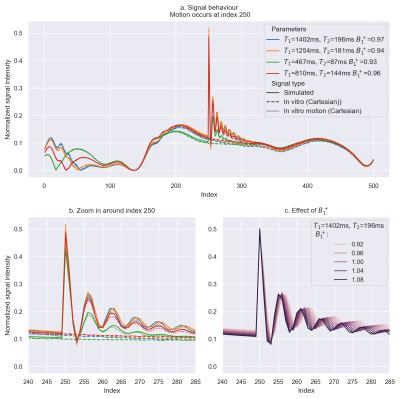
Figure 3: Top (a): Effect of motion occurring at index no. 250 for four different T1/T2 combinations using a sequence of length 5008 (see Fig.1) and a fully-sampled Cartesian acquisition. Bottom: Zoomed motion effected region (left, b) and the effect of varying $$$B_1^+$$$ on the simulated signal trajectories with motion (right c). camera-based tracking system may be possible allowing to augment the dictionary after the scan.
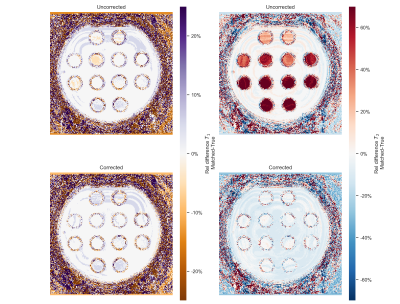
Figure 4: Left: Relative difference in T1 for dictionary matching consisting of (un-)corrected signal trajectories with respect to the ground truth. Right: The respective relative difference in T2. Controlled motion occurred at the middle of a Cartesian fully-sampled acquisition (as in Fig. 3).
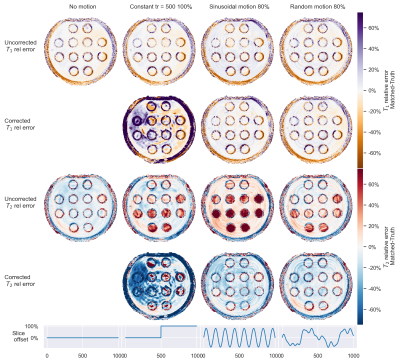
Figure 5: Comparison of relative errors in T1 and T2 for three different motion patterns (lower row) and singlespiral acquisitions with undersampling factor 32. Matching was performed with dictionaries uncorrected and corrected for the through-plane motion. A sequence of length 1000 was used to increase information contained in the data, were repeated spiral with same motion was considered less realistic.