2515

Magnetic Resonance Fingerprinting with Total Nuclear Variation Regularisation

Imraj Ravi Devia Singh¹, Olivier Jaubert¹, Bangti Jin¹, Kris Thielemans², and Simon Arridge¹
¹Department of Computer Science, University College London, London, United Kingdom, ²Institute of Nuclear Medicine, University College London, London, United Kingdom

Synopsis

Magnetic Resonance Fingerprinting (MRF) accelerates quantitative magnetic resonance imaging. The reconstruction can be separated into two problems: reconstruction of a set of multi-contrast images from k-space signals, and estimation of parametric maps from the set of multi-contrast images. In this study we focus on the former problem, while leveraging dictionary matching for the estimation of parametric maps. Two different sparsity promoting regularisation strategies were investigated: contrast-wise Total Variation (TV) which encourages image sparsity separately; and Total Nuclear Variation (TNV) which promotes a measure of joint edge sparsity. We found improved results using joint sparsity.

Introduction

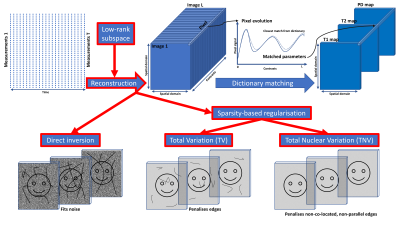
Magnetic Resonance Fingerprinting (MRF) consists of taking a set of highly under-sampled measurements of multi-contrast images. Then, on a pixel-by-pixel basis, the multi-contrast images are dictionary matched to underlying physical properties giving parametric maps. In this work, we investigate regularisation for multi-contrast image reconstruction and the effect on dictionary-matched parametric maps. In particular sparsity-based regularisation techniques are investigated such as Total Variation (TV)¹ that penalise edges; reducing noise in reconstructions.

Multi-contrast images of underlying tissue properties show significant joint structural features.² These features can be exploited through regularisation that promotes a measure of joint edge sparsity. Total Nuclear Variation (TNV) is a measure of joint edge sparsity that is known^2-4 to promote sparse, co-located, and parallel edges. It is observed that MRF multi-contrast images contain a common edge set. Therefore it is hypothesised that through TNV regularisation the accuracy of parametric maps can be increased. We propose the novel use of TNV as a measure of joint edge sparsity for MRF. This is distinct from previous work that exploits redundancy in the image contrasts,⁵ as we exploit redundancy in the image gradients (edges).

Methods

The BrainWeb phantom (200×200 pixels)^6,7 was used as ground-truth parametric maps. The maps were converted to the ground truth multi-contrast images using Extended Phase Graphs (EPG).⁸ The pulse sequence was defined as linear ramps of flip angles with constant repetition time.⁹ Between each flip angle a single radial spoke read-out is taken which is then rotated by the golden angle for the next read-out. The MRF signal is obtained by taking under-sampled k-space measurements with a non-uniform Fast Fourier Transform (nuFFT)¹⁰ of the multi-contrast images. Additive complex white Gaussian noise was added to the MRF signal to reduce the overall peak signal-to-noise to 40 dB. The dictionary was simulated using EPG for a range of realistic T1 [100:10:4000 ms] and T2 [20:2:600ms] values. The dimensionality of multi-contrast image reconstruction was reduced through projection into a low-rank subspace.^11,12 The low-rank subspace was determined by taking a singular value decomposition of the dictionary and using the first ten right singular vectors corresponding to the ten largest singular values. Each pixel is projected into this low-rank subspace resulting in ten multi-contrast singular images.TV and TNV sparsity-based regularisation techniques were implemented. TNV extends TV^1,3,4 by enforcing low-rankness in the pixel-wise Jacobian of image gradients along the images. The optimisation problem was cast:³
$$\min_{\mathbf{X}}\quad\delta_\epsilon(\mathbf{AX}-\mathbf{S})+\mathcal{R}(\nabla\mathbf{X})$$
The TV/TNV regularisation is denoted as $$$\mathcal{R}$$$ and the indicator function $$$\delta_\epsilon(\mathbf{AX}-\mathbf{S})$$$ is defined as:
$$\delta_\epsilon(\mathbf{AX}-\mathbf{S})=\begin{cases}0\quad&|\mathbf{AX}-\mathbf{S}|_2\leq \epsilon,\\\infty\quad &|\mathbf{AX}-\mathbf{S}|_2>\epsilon\end{cases}$$

where $$$\mathbf{A}$$$ is a block operator composed of forward models that combine linear operators for under-sampling, low-rank subspace projection and Fourier transform. $$$\mathbf{S}$$$ is the MRF signal and $$$\mathbf{X}$$$ are the singular images to be reconstructed. The tolerance $$$\epsilon$$$ is used as a regularisation parameter, whereby error is admitted into the data fitting term and the regularisation term $$$\mathcal{R}(\nabla\mathbf{X})$$$ is penalised more.³ The notation $$$\nabla$$$ denotes taking the image gradient. The Primal-Dual Hybrid Gradient (PDHG) algorithm¹³ was used to reconstruct both the TV and TNV due to the non-smoothness of the regularisation functionals. Direct inversion was obtained through a density compensated adjoint nuFFT. The cosine similarity metric was used to match individual pixel-wise evolutions of the singular images to a compressed dictionary entry, with the T1 and T2 values of that entry mapped back to the pixel. Proton density (PD) was determined from the scale of the pixel evolution. The framework described is illustrated in figure 1.

Results

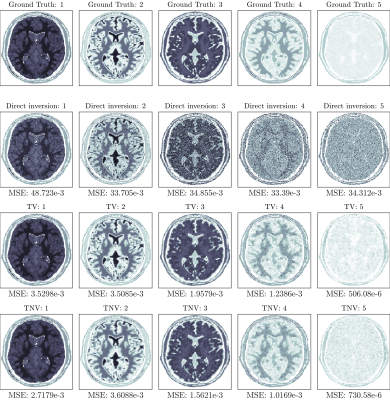
Regularised solutions were obtained with a range of $$$\epsilon$$$ values. Figure 2 gives the effect of $$$\epsilon$$$ values on the Mean Squared Error (MSE) of dictionary-matched parametric maps. The data-fitting term $$$|\mathbf{S}-\mathbf{AX}|$$$ is used to give an indication of the (inverse of) regularisation strength. Direct inversion resulted in MSE an order of magnitude larger than regularised reconstructions. TNV provided less error regardless of $$$\epsilon$$$ value for T2 and PD maps and from figure 2 TNV curves lie below TV. For T1 maps there are improvements in MSE for TNV with $$$|\mathbf{S}-\mathbf{AX}|<6.15$$$.
The first five singular images are given in Figure 3 for direct inversion, TV, and TNV solutions. The best TV solution is shown with $$$\epsilon=\sqrt{30}$$$ and the best TNV solution with $$$\epsilon=\sqrt{35}$$$. TNV reduces MSE on the first, third, and fourth singular images as compared with TV. Projection into the low-rank subspace of the dictionary concentrates the majority of statistical information into the first singular images. The parametric maps given in figure 4 show TNV outperformed TV with reductions in MSE of 2.4%, 32.6%, and 23.6% on the T1, T2, and PD maps respectively across all brain pixels. Furthermore from figure 5, there is a reduction in MSE with TNV on the majority of segmented white and gray matter parametric maps.

Discussion and Conclusion

The synergistic action of TNV, which penalises rank-two pixel-wise Jacobians such that they are rank-one, aligns the edge set along singular images. This results in an appreciable reduction in MSE on parametric maps as compared with TV. Sparsity-based synergistic regularisation presents a method to increase the accuracy of reconstructed parametric maps for MRF. Code and data are available at github.com/Imraj-Singh/MRF_TNV_LR.

Acknowledgements

This work was supported by EPSRC Centre for Doctoral Training in Intelligent, Integrated Imaging In Healthcare (EP/S021930/1). Freely available software from^8,10,14,15 was utilised in this research.

References

1. Rudin, L. I., Osher, S., & Fatemi, E. (1992). Nonlinear total variation based noise removal algorithms. In Physica D: Nonlinear Phenomena (Vol. 60, Issues 1–4, pp. 259–268). Elsevier BV. https://doi.org/10.1016/0167-2789(92)90242-f

2. Arridge, S. R., Ehrhardt, M. J., & Thielemans, K. (2021). (An overview of) Synergistic reconstruction for multimodality/multichannel imaging methods. In Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences (Vol. 379, Issue 2200, p. 20200205). The Royal Society. https://doi.org/10.1098/rsta.2020.0205

3. Rigie, D. S., & La Rivière, P. J. (2015). Joint reconstruction of multi-channel, spectral CT data via constrained total nuclear variation minimization. In Physics in Medicine and Biology (Vol. 60, Issue 5, pp. 1741–1762). IOP Publishing. https://doi.org/10.1088/0031-9155/60/5/1741

4. Duran, J., Moeller, M., Sbert, C., & Cremers, D. (2016). Collaborative Total Variation: A General Framework for Vectorial TV Models. In SIAM Journal on Imaging Sciences (Vol. 9, Issue 1, pp. 116–151). Society for Industrial & Applied Mathematics (SIAM). https://doi.org/10.1137/15m102873x

5. Bustin, A., Lima da Cruz, G., Jaubert, O., Lopez, K., Botnar, R. M., & Prieto, C. (2019). High-dimensionality undersampled patch-based reconstruction (HD-PROST) for accelerated multi-contrast MRI. In Magnetic Resonance in Medicine (Vol. 81, Issue 6, pp. 3705–3719). Wiley. https://doi.org/10.1002/mrm.27694

6. Aubert-Broche, B., Evans, A. C., & Collins, L. (2006). A new improved version of the realistic digital brain phantom. In NeuroImage (Vol. 32, Issue 1, pp. 138–145). Elsevier BV. https://doi.org/10.1016/j.neuroimage.2006.03.052

7. Aubert-Broche, B., Griffin, M., Pike, G. B., Evans, A. C., & Collins, D. L. (2006). Twenty New Digital Brain Phantoms for Creation of Validation Image Data Bases. In IEEE Transactions on Medical Imaging (Vol. 25, Issue 11, pp. 1410–1416). Institute of Electrical and Electronics Engineers (IEEE). https://doi.org/10.1109/tmi.2006.883453

8. Weigel, M. (2014). Extended phase graphs: Dephasing, RF pulses, and echoes - pure and simple. In Journal of Magnetic Resonance Imaging (Vol. 41, Issue 2, pp. 266–295). Wiley. https://doi.org/10.1002/jmri.24619

9. Gómez, P. A., Cencini, M., Golbabaee, M., Schulte, R. F., Pirkl, C., Horvath, I., Fallo, G., Peretti, L., Tosetti, M., Menze, B. H., & Buonincontri, G. (2020). Rapid three-dimensional multiparametric MRI with quantitative transient-state imaging. In Scientific Reports (Vol. 10, Issue 1). Springer Science and Business Media LLC. https://doi.org/10.1038/s41598-020-70789-2

10. Fessler, J. A., & Sutton, B. P. (2003). Nonuniform Fast Fourier Transforms using min-max interpolation. In IEEE Transactions on Signal Processing (Vol. 51, Issue 2, pp. 560–574). Institute of Electrical and Electronics Engineers (IEEE). https://doi.org/10.1109/tsp.2002.807005

11. McGivney, D. F., Pierre, E., Ma, D., Jiang, Y., Saybasili, H., Gulani, V., & Griswold, M. A. (2014). SVD Compression for Magnetic Resonance Fingerprinting in the Time Domain. In IEEE Transactions on Medical Imaging (Vol. 33, Issue 12, pp. 2311–2322). Institute of Electrical and Electronics Engineers (IEEE). https://doi.org/10.1109/tmi.2014.2337321

12. Assländer, J., Cloos, M. A., Knoll, F., Sodickson, D. K., Hennig, J., & Lattanzi, R. (2017). Low rank alternating direction method of multipliers reconstruction for MR fingerprinting. In Magnetic Resonance in Medicine (Vol. 79, Issue 1, pp. 83–96). Wiley. https://doi.org/10.1002/mrm.26639

13. Chambolle, A., & Pock, T. (2010). A First-Order Primal-Dual Algorithm for Convex Problems with Applications to Imaging. In Journal of Mathematical Imaging and Vision (Vol. 40, Issue 1, pp. 120–145). Springer Science and Business Media LLC. https://doi.org/10.1007/s10851-010-0251-1

14. Golbabaee, M., Buonincontri, G., Pirkl, C. M., Menzel, M. I., Menze, B. H., Davies, M., & Gómez, P. A. (2021). Compressive MRI quantification using convex spatiotemporal priors and deep encoder-decoder networks. In Medical Image Analysis (Vol. 69, p. 101945). Elsevier BV. https://doi.org/10.1016/j.media.2020.101945

15. Mazor, G., Weizman, L., Tal, A., & Eldar, Y. C. (2018). Low-rank magnetic resonance fingerprinting. In Medical Physics (Vol. 45, Issue 9, pp. 4066–4084). Wiley. https://doi.org/10.1002/mp.13078

Figures

Illustrative diagram of the framework developed. The linear inverse problem of multi-contrast reconstruction was investigated with sparsity-based regularisation techniques. Total variation promotes edge sparsity, whereas total nuclear variation promotes joint edge sparsity.

The colours correspond to blue: total variation and red: total nuclear variation. The lowest error for TV and TNV was with $$$\epsilon=\sqrt{30}$$$ and $$$\epsilon=\sqrt{35}$$$ respectively. The data-fitting value gives an indication of the (inverse of) the regularisation strength. The mean squared error (MSE) is of the corresponding parametric maps on the whole brain.

The first five ground truth singular images with the images reconstructed with direct inversion, total variation ($$$\epsilon=\sqrt{30}$$$), and total nuclear variation ($$$\epsilon=\sqrt{35}$$$). The mean squared error (MSE) is of the corresponding singular images on the whole brain. The colour bar limits were kept consistent between the same singular images.

Dictionary matched parametric maps from singular images reconstructed with direct inversion, total variation ($$$\epsilon=\sqrt{30}$$$), and total nuclear variation ($$$\epsilon=\sqrt{35}$$$). The mean squared error (MSE) is of the corresponding parametric maps on the whole brain. The colour bar limits were kept consistent between the same parametric maps.

Mean squared error (MSE) results on white and gray matter with best performing TV and TNV regularisation, $$$\epsilon=\sqrt{30}$$$ and $$$\epsilon=\sqrt{35}$$$ respectively.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

2515

DOI: https://doi.org/10.58530/2022/2515