Introduction

Many neurological diseases, such as multiple sclerosis and Alzheimer's disease, have been linked to increased permeability of the blood brain barrier (BBB)¹. MRI has the potential to detect and monitor dysfunction of the BBB in-vivo non-invasively. Current techniques often have low SNR, require the use of contrast agents, or give only global measurements: we propose a method for voxel-wise quantification of blood volume ($$$\nu_b$$$) and BBB water exchange (by quantifying capillary water residence time ($$$\tau_b$$$)), as a metric of BBB function/dysfunction, using magnetic resonance fingerprinting (MRF)². We simulate a spoiled gradient echo (SPGR) MRF acquisition to study the ability to measure $$$\nu_b$$$ and $$$\tau_b$$$ by exploiting differences in native longitudinal relaxation between blood and tissue and explore the impact of noise on the method’s accuracy and precision.

Methods

An array of spin isochromats were simulated assuming a two-site exchange system, intra- and extra-vascular, with defined compartmental volumes and a semipermeable barrier representing the BBB allowing for two-way exchange. The Bloch equations were used to simulate signals arising from this array as its magnetisation evolves over time. Signal 'fingerprints' were generated by varying input flip angle ($$$\alpha$$$) and repetition time (TR), while assuming a short and unvarying TE = 8ms. A pulse train of 1000 TR repetitions was modelled so that a single 2D slice with single shot spiral readout could be achieved in a 10-minute scan. We assumed that the noise in MRF signals could be modelled as zero-mean complex Gaussian noise with a standard deviation. $$$\sigma_G$$$. on each isochromat. Each isochromat has an equilibrium magnetization of unity therefore $$$\sigma_G = 0.01$$$ is equivalent to 1% noise on the equilibrium magnetization.

Three sets of experiments were performed. First, a comparison of a non-optimised and optimised dictionary: both dictionaries contained a variation in blood volume from 1 to 10% in steps of 1%, denoted $$$\nu_b = [min=1:step=1:max=10]$$$% and residence time of water in the intra-vascular compartment, $$$\tau _b =[200:100:1600]$$$ ms. Initial, ‘non-optimised’ values for $$$\alpha$$$ and TR were chosen to closely match the variation chosen by Ma et al.² Optimisation was performed using a branch and bound technique to optimise $$$\alpha$$$ and TR variation to maximise the difference between signals associated with the range of $$$\tau_b$$$³. Second, a sample data set with variation along $$$\nu_b([1:1:10]$$$%), $$$\tau_b([200:100:1600]$$$ms), T₁ of blood: $$$T_{1,b}([1500:200:1900]$$$ ms), T₁ of the extravascular space: $$$T_{1,e}([1000:200:2000]$$$ms), and $$$B^+_1([0.8:0.1.1.2] \times B_1$$$), was then matched to the $$$\nu_b$$$ and $$$\tau_b$$$ - only dictionary with fixed values of $$$T_{1,e}$$$, $$$T_{1,b}$$$, $$$B^+_1$$$ and from the literature, to explore robustness of matching when these parameters are not known a priori. Third, the five-dimensional sample was matched to a dictionary of the same dimensionality to test the feasibility of determining each parameter simultaneously.

Results

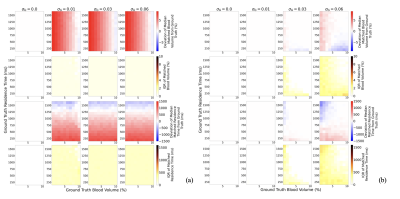
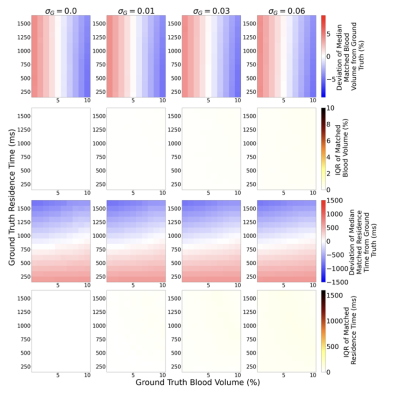
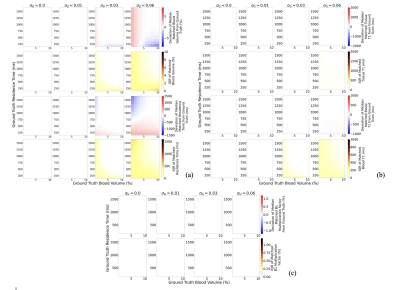
Experiment 1: Not optimising the sequence specifically for the quantification of $$$\nu_b$$$ and $$$\tau_b$$$ is not viable as there is no robustness to noise: introduction of 1% noise leads to an average $$$\nu_b$$$ discrepancy of 4.03 % and 474 ms for $$$\tau_b$$$ (Figure 1a); when optimised there is a significant improvement in the robustness of $$$\nu_b$$$ and $$$\tau_b$$$ matching to noise (average of 0.00 % discrepancy and 0.03 ms, respectively) (Figure 1b). Experiment 2: Assuming literature values for $$$T_{1,e}, T_{1,b}$$$ and no variation in $$$B_1$$$, when variation is present leads to large errors, regardless of noise levels (Figure 2). Experiment 3: Figure 3 suggests that it is feasible to measure $$$T_{1,e}, T_{1,b}$$$ and $$$B_1^+$$$ simultaneously with $$$\nu_b$$$ and $$$\tau_b$$$ using a 5-dimensional dictionary at reasonable noise levels. The impact on the accuracy of matching $$$\nu_b$$$ and $$$\tau_b$$$ when introducing these extra dimensions is minimal: at 3% noise these additional dimensions only increase average discrepancy in $$$\nu_b$$$ and $$$\tau_b$$$ matching from 0.10%/18.8ms to 0.12%/24.3ms respectively.

Discussion

Our simulations indicate promise for MRF quantification of $$$\nu_b$$$, $$$\tau_b$$$, $$$T_{1,e}$$$, $$$T_{1,b}$$$ and $$$B^+_1$$$ simultaneously. Substantial changes in signal magnitude caused by the $$$T_1$$$ values and field inhomogeneities seem to minimally interfere with smaller changes in signal shape caused by blood-water effects within the 5-dimensional dictionary. The noise limit for this technique is around 3% of the equilibrium magnetisation, which is comparable with fully sampled voxel-wise noise levels in the MRF literature. Further work will include experimental data acquisition to confirm the findings of these simulations.

Conclusion

Simulations suggest that it is possible to optimise an SPGR MRF acquisition for the quantification of blood volume and residence time of water in blood, simultaneously with $$$T_{1,e}, T_{1,b}$$$ and $$$B^+_1$$$. This indicates promise for efficient in vivo measurements.

Acknowledgements

This work is supported by the EPSRC-funded UCL Centre for Doctoral Training in Medical Imaging (EP/S021930/1) and EPSRC grant number EP/S031510/1.