2466

On the water–fat in-phase assumption for quantitative susceptibility mapping (QSM)

Christof Boehm¹, Jakob Meineke², Kilian Weiss³, Marcus R Makowski¹, and Dimitrios C Karampinos¹
¹Department of Diagnostic and Interventional Radiology, School of Medicine, Klinikum Rechts der Isar, Technical University of Munich, Munich, Germany, ²Philips Research, Hamburg, Germany, ³Philips GmbH Market DACH, Hamburg, Germany

Synopsis

Gradient echo imaging using in-phase echoes has been proposed to reduce the field-map estimation in water–fat regions to a convex nonlinear least squares problem. Conventionally, the in-phase assumption is based on a single-peak fat-model. However, fat is known to have a complex spectrum rendering the definition of in-phase echo times problematic. In this work, the single-fat-peak in-phase assumption is replaced by a multi-peak effective in-phase assumption. QSM based on multi-peak in-phase echo times is shown to yield similar results to water–fat imaging based field- and susceptibility-mapping in a simulation and in vivo in the spine and the breast.

Introduction

Quantitative susceptibility mapping (QSM)¹ has been applied in$$$\;$$$tissues outside the brain, e.g.$$$\;$$$to distinguish osteolytic/osteoblastic bone changes in the spine², to characterize lesions and calcifications in breast disease^1,3, to measure bone density^4,5 or liver iron overload^6,7,8.
Gradient-echo imaging using only in-phase echoes has been proposed for$$$\;$$$the estimation of susceptibility in the body⁹. Forthe definition of in-phase echo times a single-peak fat-model is$$$\;$$$assumed. When using in-phase echo times, the signal model is$$$\;$$$convex within the period of the phasor and thus the field-map can robustly be$$$\;$$$estimated using nonlinear least squares techniques. However, the$$$\;$$$fat spectrum is$$$\;$$$known to$$$\;$$$be spectrally complex rendering the definition of in-phase echo$$$\;$$$times problematic. Furthermore, it has$$$\;$$$been shown that QSM using single-fat-peak based in-phase echoes can$$$\;$$$introduce significant quantification bias¹⁰. In$$$\;$$$this work the correlation between field-map estimation bias and susceptibility bias$$$\;$$$is investigated first in$$$\;$$$general, and$$$\;$$$then specifically for$$$\;$$$the single-peak in-phase assumption. Furthermore the$$$\;$$$use of$$$\;$$$a multi-peak fat-model effective in-phase echoes is$$$\;$$$proposed and$$$\;$$$tested in-silico and in-vivo in the spine and the breast.

Methods

Multi-peak effective in-phase echo times
The multi-peak signal model reads:$$\boldsymbol{s}(t_n)=\left(\rho_W+c_n\rho_F\right)e^{\gamma{t_n}},\quad\gamma=i2\pi{f_B}-R_2^*\\c_n=\sum_{p=1}^{P}a_p e^{i2\pi\Delta{f_p}t_n},\quad\text{with}\quad\sum_{p=1}^{P}a_p=1,$$ where $$$t_1,t_2,...,t_N$$$ different echo times,$$$\;f_B$$$ field-map,$$$\;\rho_W\;$$$and $$$\rho_F$$$ complex signal of$$$\;$$$the water and fat components with$$$\;$$$an equal transverse relaxation rate$$$\;{R}_2^*$$$. The$$$\;$$$fat spectrum is$$$\;$$$assumed to have $$$P$$$ spectral peaks with corresponding relative amplitudes $$$a_p\;$$$and chemical shift $$$\Delta f_p$$$.$$$\;$$$For the definition of$$$\;$$$in-phase echo times, only one spectral peak $$$P=1\;$$$is assumed. Thus, water and$$$\;$$$fat are in-phase when$$$\;$$$the fat-phasor is zero and$$$\;$$$the condition $$$\Delta{f}\cdot{t=n},\;n\in\mathbf{N}$$$ is$$$\;$$$met. In$$$\;$$$the case$$$\;$$$of multiple fat-peaks in-phase echo times generally do$$$\;$$$not exist. However, effective in-phase echoes do$$$\;$$$exist meaning the timepoints, where the fatphasor is $$$\angle{c_{n}}=0$$$. The effective multi-peak in-phase echo times are generally not equidistant and change with the employed fat-model.
Single Voxel Simulation
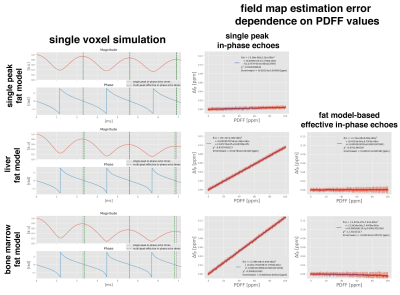
For$$$\;$$$the estimation of$$$\;$$$the difference between conventional single-peak and effective multi-peak fat-model a$$$\;$$$single-voxel simulation was performed using Eq.1 with either$$$\;$$$a single peak fat-model ($$$\Delta{f}=434\;$$$[Hz]), a fat-model specific to bone marrow¹¹, a$$$\;$$$model specific to$$$\;$$$the liver¹², a$$$\;$$$fat fraction of 70%,$$$\;R_{2}^{*}=30\;$$$[Hz] and $$$f_{B}$$$=0. For above bone marrow and liver model, the first 3 effective in-phase echo times were found to be equidistant in scanner time precision (0.01ms) and are TE=$$$[2.38,4.60,6.82]\;$$$ms and TE=$$$[2.35, 4.59, 6.83]\;$$$ms, respectively.
Monte Carlo Simulation
For the assessment of$$$\;$$$the field-map estimation error with$$$\;$$$fat fraction using$$$\;$$$both conventional single-peak or effective multi-peak in-phase echotimes a$$$\;$$$Monte Carlo simulation was performed. The$$$\;$$$fat fraction values were varied from 0 to 100%, an SNR of 100, $$$R_{2}^{*}=30\;$$$[Hz] and $$$f_{B}$$$=0 were$$$\;$$$used.
Correlation between field-map estimation error and susceptibility quantification bias
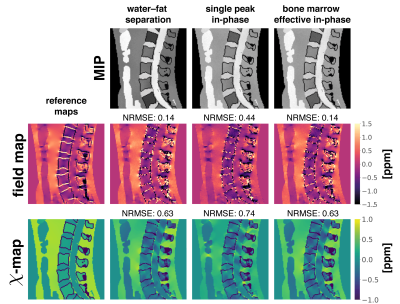
For the assessment of the quantification bias in a realistic anatomy, a$$$\;$$$numerical simulation based on$$$\;$$$the Duke phantom was performed¹⁰. Each tissue was assigned with$$$\;$$$either their literature value or$$$\;$$$values extracted from in$$$\;$$$vivo scans and forward simulated using Eq.(1) and either conventional water–fat separation echo times with$$$\;$$$6 echoes,$$$\;\text{TE}_{\text{min}}/\Delta{\text{TE}}=1.0\:$$$ms, conventional single-peak in-phase echo times$$$\;$$$or effective in-phase echo times for$$$\;$$$the two above mentioned fat-models. A$$$\;$$$background field was$$$\;$$$not simulated to allow for$$$\;$$$the estimation of$$$\;$$$the quantification bias$$$\;$$$of the$$$\;$$$local field-map only. Complex Gaussian noise was$$$\;$$$added to the$$$\;$$$data (SNR$$$\;$$$100). The field-map, water(–fat)-images and $$$R_2^*\;$$$-map were estimated using graph-cut algorithm¹³. The field-maps were inverted to$$$\;$$$a susceptibility-map using the recently proposed wfTFI method².
In vivo measurements
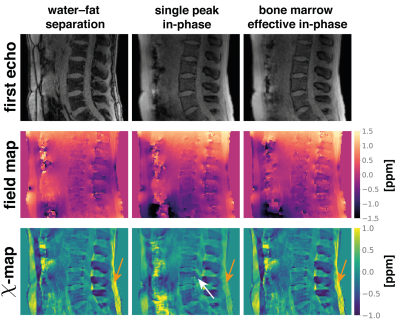
The aformentioned processing of$$$\;$$$graph-cut-based field-mapping followed by wfTFI QSM was applied to$$$\;$$$in vivo spine$$$\;$$$and breast scans$$$\;$$$of$$$\;$$$2 healthy volunteers. Scanning was performed on a 3$$$\:$$$T scanner (Ingenia$$$\;$$$Elition, Philips$$$\;$$$Healthcare, Best, The Netherlands) using a$$$\;$$$monopolar time-interleaved multi-echo gradient-echo sequence¹⁴.

Results

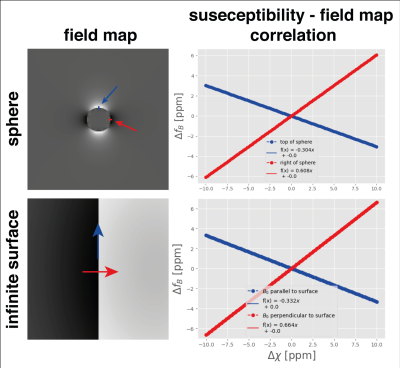
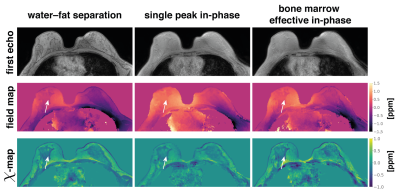
Using conventional single-peak in-phase echo times in$$$\;$$$a more realistic multi-peak environment, the$$$\;$$$fat phasor is$$$\;$$$not zero at$$$\;$$$the measured time points (Fig.1,$$$\;$$$column$$$\;$$$1). This introduces a field-map estimation bias of over 0.12$$$\;$$$ppm for voxels containing only fat (Fig.1, column 2). The$$$\;$$$use of effective multi-peak in-phase echo times can$$$\;$$$reduce error to the noise floor (Fig.1, column 3). The slope of the correlation between susceptibility differences and field-map differences at a spherical or infinite surface yields almost exactly the dominant values of the dipole kernel($$$-\dfrac{1}{3},\dfrac{2}{3}$$$)(Fig.2). The inverse of these values can hence be$$$\;$$$used to$$$\;$$$estimate susceptibility error from field-map estimation error. Meaning that the above 0.12$$$\;$$$ppm field-map estimation error$$$\;$$$can translate to an error of 0.36$$$\;$$$ppm in the susceptibility estimation.
In$$$\;$$$the numerical simulation of$$$\;$$$a lumbar spine, effective multi-peak in-phase echo$$$\;$$$times achieve the$$$\;$$$same accuracy in field- and susceptibility-mapping as based on water-fat separation, while the single-peak in-phase estimates show significant quantification bias (Fig.3). In an$$$\;$$$in vivo spine scan, field-map estimation error$$$\;$$$in the single-peak in-phase pipeline propagates non-locally, as$$$\;$$$shown in the cerebrospinal fluid region (Fig.4). Effective multi-peak in-phase echos$$$\;$$$yield similar results to water-fat separation based maps. In an in vivo breast scan (Fig.5), the contrast$$$\;$$$in the right breast between fat$$$\;$$$and fibroglandular tissue$$$\;$$$is lost$$$\;$$$in QSM and the field-map using single-peak in-phase echoes, while effective multi-peak in-phase echos$$$\;$$$again yield similar results$$$\;$$$to water-fat separation based maps and$$$\;$$$a good delineation between tissue types.

Discussion

The$$$\;$$$use of effective multi-peak in-phase echo times$$$\;$$$can eliminate the field-map quantification bias introduced by$$$\;$$$the single-peak in-phase assumption. Although, effective multi-peak in-phase echo times$$$\;$$$are generally not equidistant a set of$$$\;$$$3 equidistant echo$$$\;$$$times can be$$$\;$$$found within scanner timing precision$$$\;$$$(0.01ms) for commonly used liver$$$\;$$$and bone marrow fat-models.
The$$$\;$$$use of single-peak in-phase echoes introduces significant bias$$$\;$$$in the field-map, which, importantly, is voxel-wise dependent on$$$\;$$$the fat$$$\;$$$fraction.

Conclusion

Effective multi-peak in-phase echo times can$$$\;$$$be used for the quantification of susceptibility in body regions with$$$\;$$$a bias not$$$\;$$$greater than water–fat separation based estimation and overcome the$$$\;$$$limitations of single-peak in-phase echo times$$$\;$$$for susceptibility mapping in$$$\;$$$regions with fatty$$$\;$$$tissue.

Acknowledgements

The present work was supported by the European Research Council (grantagreement No 677661, ProFatMRI). The authors also acknowledge research sup-port from Philips Healthcare.

References

[1] Wang Y, Liu T. Quantitative Susceptibility Mapping (QSM): Decoding MRI Data for a Tissue Magnetic Biomarker. Magnetic Resonance in Medicine 2014; 73:82–101. 10.1002/mrm.25358.

[2] Boehm C, Sollmann N, Meineke J, Ruschke S, Dieckmeyer M, Weiss K, Zimmer C, Makowski MR, Baum T, Karampinos DC. Preconditioned water-fattotal field inversion: Application to spine quantitative susceptibility mapping. ; https://doi.org/10.1002/mrm.28903.

[3] Schweser F, Hermann KH, Deistung A, Atterbury M, Baltzer PA, Burmeis-ter HP, Kaiser WA, Reichenbach JR. Quantitative Magnetic Susceptibility Mapping (QSM) in Breast Disease Reveals Additional Information for MR-Based Characterization of Carcinoma Calcification. In: Proceedings 19.Annual Meeting International Society for Magnetic Resonance in Medicine, Montreal, 2011. p. 1014.

[4] Dimov AV, Liu Z, Spincemaille P, Prince MR, Du J, Wang Y. Bone Quantitative Susceptibility Mapping Using a Chemical Species-Specific R2* Signal Model With Ultrashort and Conventional Echo Data. Magnetic Resonance in Medicine 2017; 79:121–128. 10.1002/mrm.26648.

[5] Diefenbach MN, Meineke J, Ruschke S, Baum T, Gersing A, Karampinos DC. On the Sensitivity of Quantitative Susceptibility Mapping for Measuring Trabecular Bone Density. Magnetic Resonance in Medicine 2018; . 10.1002/mrm.27531.

[6] Sharma SD, Hernando D, Horng DE, Reeder SB. Quantitative Susceptibility Mapping in the Abdomen As an Imaging Biomarker of Hepatic Iron Overload. Magnetic Resonance in Medicine 2014; 74:673–683.10.1002/mrm.25448.

[7] Lin H, Wei H, He N, Fu C, Cheng S, Shen J, Wang B, Yan X, Liu C,Yan F. Quantitative Susceptibility Mapping in Combination With Water–Fat Separation for Simultaneous Liver Iron and Fat Fraction Quantification.European Radiology 2018; 28:3494–3504. 10.1007/s00330-017-5263-4.

[8] Jafari R, Sheth S, Spincemaille P, Nguyen TD, Prince MR, Wen Y, Guo Y,Deh K, Liu Z, Margolis D, Brittenham GM, Kierans AS, Wang Y. Rapid Automated Liver Quantitative Susceptibility Mapping. Journal of Magnetic Resonance Imaging 2019; 50:725–732. 10.1002/jmri.26632.

[9] Guo Y, Liu Z, Wen Y, Spincemaille P, Zhang H, Jafari R, Zhang S, Eskreis-Winkler S, Gillen KM, Yi P, Feng Q, Feng Y, Wang Y. Quantitative susceptibility mapping of the spine using in-phase echoes to initialize inhomogeneous field and R2* for the nonconvex optimization problem off at-water separation. NMR in Biomedicine 2019; 32:e4156. e4156 NBM-19-0042.R2, https://doi.org/10.1002/nbm.4156.

[10] Boehm C, Diefenbach MN, Kronthaler S, Meineke J, Weiss K,Makowski MR, Karampinos DC. Quantitative susceptibility mapping in water-fat regions using in-phase echoes introduces significant quantification bias. In: Proceedings 30. Annual Meeting International Society for Magnetic Resonance in Medicine, Online, 2021. p. 3972.

[11] Ren J, Dimitrov I, Sherry AD, Malloy CR. Composition of Adipose Tissue and Marrow Fat in Humans By1h Nmr At 7 Tesla. Journal of Lipid Research 2008; 49:2055–2062. 10.1194/jlr.d800010-jlr200.

[12] Hamilton G, Yokoo T, Bydder M, Cruite I, Schroeder ME, Sirlin CB, Middleton MS. In Vivo Characterization of the Liver Fat 1h Mr Spectrum. NMR in Biomedicine 2010; 24:784–790. 10.1002/nbm.1622.

[13] Boehm C, Diefenbach MN, Makowski MR, Karampinos DC. ImprovedBody Quantitative Susceptibility Mapping By Using a Variable-layerSingle-min-cut Graph-cut for Field-mapping. Magnetic Resonance inMedicine 2020; nil:mrm.28515. 10.1002/mrm.28515.

[14] Ruschke S, Eggers H, Kooijman H, Diefenbach MN, Baum T, Haase A,Rummeny EJ, Hu HH, Karampinos DC. Correction of Phase Errorsin Quantitative Water–Fat Imaging Using a Monopolar Time-InterleavedMulti-Echo Gradient Echo Sequence. Magnetic Resonance in Medicine2016; 78:984–996. 10.1002/mrm.26485.

Figures

Figure 1: The first column shows the signal evolution for the corresponding fat models. The gray dashed lines show the conventional in-phase echo times (∆t = 2.3ms), while the green dashed lines show the timepoints, when the fat phasor is zero. Although the echo times seem to be very close, the field-map estimation bias with fat fraction can be significant using the above single-peak echo times as depicted in column 2. When using the 3 equidistant effective in-phase echo times for the corresponding model, the error can be reduced to the noise floor as shown in column 3.

Figure 2: Forward simulation from susceptibility to field-map of a sphere with a susceptibility difference from inside and outside and of a infinite surface of two substances with different susceptibility. The slope of the correlation between susceptibility differences and field-map differences yields almost the dominant values of the dipole kernel (-1/3,2/3). The values for the sphere and for infinite surface vary only slightly. The inverse of both values can subsequently be used for the calculation of susceptibility quantification bias introduced by field-mapping bias.

Figure 3: Numerical simulation results in a lumbar spine. Field-map and QSM results show a significant quantification bias when using in-phase echoes of a 214% higher error in the field-map and 17% higher error in the susceptibility map when compared to water–fat separation based quantification. The overall contrast of the QSM map is reduced using single-peak in-phase echo times mainly driven by the reduced contrast of regions with high fat fraction. When using effective multi-peak in-phase echotimes, the estimation bias is similar to water–fat separation based quantification.

Figure 4: Healthy spine results are in good agreement with the numerical spine simulation. Regions with high fat, such as the subcutaneous fat (orange arrow), are significantly underestimated in the susceptibility map based on single-peak in-phase echoes. In the cerebrospinal fluid (CSF) and in proximity to high fat regions between the spinal processes the susceptibility shows non local streaking artifacts (white arrow) dominating the CSF. When using effective multi-peak in-phase echoes the susceptibility values in both regions are similar to water-fat separation based QSM.

Figure 5: In vivo breast result show that the delineation of fatty tissue from other breast tissue is limited in the field- and χ-map (arrows) when using only single-peak in-phase echoes. When using effective multi-peak in-phase echotimes similar results to the water–fat separation based susceptibility-mapping can be achieved. However, in the susceptibility map based on effective multi-peak in-phase echo times an increase of noise can be seen. This increase in noise is related to the reduced number of available echoes (3 vs 6).

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

2466

DOI: https://doi.org/10.58530/2022/2466