2461

Nonlinear multi-echo dipole inversion

Christian Kames^1,2, Jonathan Doucette^1,2, and Alexander Rauscher^1,2,3
¹UBC MRI Research Centre, University of British Columbia, Vancouver, BC, Canada, ²Department of Physics and Astronomy, University of British Columbia, Vancouver, BC, Canada, ³Department of Pediatrics, University of British Columbia, Vancouver, BC, Canada

Synopsis

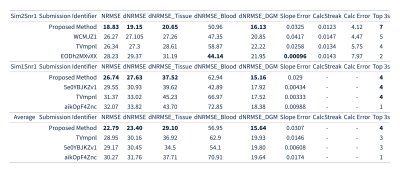
We propose a two-pass multi-echo nonlinear dipole inversion method. In the first pass an initial susceptibility map is obtained. The susceptibility map is then further processed by deconvolving the residual of the forward computed phase and the input phase to recover remnant low frequency susceptibility sources. The proposed method attains a NRMSE of 18.8 on the QSM Reconstruction Challenge 2.0 calcification dataset (Sim2Snr1), decisively outperforming the best scoring submissions of the challenge (NRMSE 26.3, 28.3, 28.5).

Introduction

Quantitative susceptibility mapping (QSM) aims to estimate the tissue magnetic susceptibility distribution from MR phase images. In multi-echo acquisitions, the MR signal is measured at multiple echo times (TEs) yielding multiple samples of the underlying susceptibility distribution. To obtain the susceptibility map from these samples, either the frequency map is computed from the multi-echo phase images, using a linear or nonlinear fit¹, or each echo is processed individually and the resulting susceptibility maps are independently analyzed or averaged. Due to noise and unwrapping errors, frequency map estimation methods can introduce errors in the frequency map and even change its noise model. The recently proposed multi-echo complex total field inversion method (mcTFI)² aims to bypass these errors by computing the susceptibility distribution directly from the complex signal. While mcTFI shows promising results, the formulated optimization problem is challenging, as it solves for the initial magnetization, $$$R_2^*$$$, and the initial phase offset alongside the susceptibility map and thus requires precise initial guesses. In this work, we propose a simpler multi-echo nonlinear field inversion method.

Methods

Assuming an isotropic susceptibility distribution, and ignoring noise for simplicity, the phase acquired at echo time $$$TE_j$$$ is defined as:$$\varphi_{j}=2\pi TE_j f+\varphi_0=2\pi TE_j\gamma B_0D\chi +\varphi_0,$$where $$$f$$$ is the magnetization field (frequency map), $$$\gamma$$$ is the gyromagnetic ratio, $$$B_0$$$ is the main field strength, $$$D$$$ is the dipole kernel convolution matrix, $$$\chi$$$ is the susceptibility map, and $$$\varphi_0$$$ is the initial phase offset.Rather than first estimating $$$f$$$ and then solving the ill-posed dipole inversion, we propose the following nonlinear optimization problem:$$\chi^*=\underset{\chi}{\text{argmin }}\sum_{j=1}^{N_{TE}}\frac{1}{2}||W_j(e^{i2\pi\gamma B_0 TE_j D\chi}-e^{i\varphi_j})||+\lambda\text{ }TV(\chi),$$where $$$W_j$$$ is a weighting matrix, in this work the normalized magnitude of the $$$j$$$th echo, $$$\lambda$$$ is a regularization parameter, and $$$TV(\chi)$$$ is the total variation regularizer. The optimization problem is solved using an ADMM method³. We further utilize a two-pass approach in order to recover remnant low-frequency susceptibility sources that were not included in the initial susceptibility map, $$$\chi^*$$$, due to regularization. To do so we first compute the residual $$$\Delta \varphi_i$$$ of the acquired phase and the forward computed phase from the initial susceptibility map:$$\Delta\varphi_j=\varphi_j - 2\pi TE_j\gamma B_0D\chi^*.$$Then we solve the optimization problem a second time with a reduced regularization parameter:$$\Delta\chi^*=\underset{\Delta\chi}{\text{argmin }}\sum_{j=1}^{N_{TE}}\frac{1}{2}||W_j(e^{i2\pi\gamma B_0 TE_j D\Delta\chi}-e^{i\Delta\varphi_j})||+\lambda_\Delta TV(\chi),$$where $$$\lambda_\Delta < \lambda$$$. Because we use a smaller regularization parameter, the susceptibility map will be contaminated with streaking artifacts and noise. To remove these artifacts we apply a box filter of size 3x3x3, $$$h$$$, to $$$\Delta\chi$$$. The final susceptibility map is then given by:$$\chi=\chi^*+h*\Delta\chi.$$

Results

We validated the proposed method on the two QSM Reconstruction Challenge 2.0 (RC2) datasets (Sim2Snr1, Sim1Snr1)^4,5 using the official metrics.

Data-processing: The multi-echo phase images were first unwrapped using ROMEO⁶, zero-padded to a matrix size of 196x240x240, and normalized by dividing each echo by its echo time and multiplying it by a factor of $$$TE_2-TE_1=0.008s$$$. The unmasked phase and magnitude images were then used to compute the susceptibility map. The regularization parameters used were $$$\lambda = 5.1e$$$-4 for the first pass, and $$$\lambda_\Delta=\lambda/3$$$ for the second pass. The stopping criterion was $$$||\chi^{k+1}-\chi^k||_2/||\chi^{k+1}||_2<3e$$$-5. Additionally, a Gaussian filter ($$$\sigma=0.5$$$) was applied to $$$\chi^*$$$ before computing the residual phase images. To combat over-smoothing due to the filter, a Gaussian filter with a smaller standard deviation ($$$\sigma=0.4$$$) was applied to $$$\chi^*$$$ before adding $$$\Delta\chi$$$.

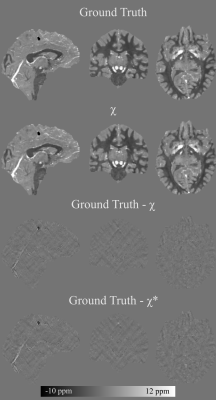
Validation: The susceptibility maps computed during the two-pass approach are shown in Figure 1. Figure 2 shows the difference map with the ground truth susceptibility map. The first pass is already successful in reconstructing the susceptibility sources with errors confined to veins and the calcification. The second pass corrects the susceptibility values in the veins but is unable to correct the calcification. The official reconstruction challenge metrics are shown in Table 1, along with the top 3 NRMSE scores for each dataset. The proposed method achieves the most top 3 scores on either dataset and outperforms all other solutions on the NRMSE metrics. While the reconstructed Sim2Snr1 susceptibility map scores considerably better compared to the other submissions than the Sim1Snr1 map, both datasets score poorly on the Slope Error metric.

Discussion and Conclusion

We proposed a two-pass nonlinear multi-echo dipole inversion method. The multi-echo field inversion formulation takes advantage of the multiple samples of the susceptibility distribution acquired in a multi-echo acquisition. On the RC2 Sim2Snr1 calcification dataset, the proposed method attains a NRMSE of 22.0, outperforming the best scoring submission of the challenge (NRMSE 26.3). By incorporating a second pass to recover remnant susceptibility sources which were regularized out, we can further reduce the NRMSE to 18.8, and could even further drop it to 18.3 if we over-smooth the image, which, however, may be undesirable. The problem formulation is relatively simplistic in that it uses a simple total variation regularizer without regularization weights or involved data fidelity weights. As such, we believe that there are still substantial gains to be made. Furthermore, the second pass, while effective and seemingly robust, is crudely constructed, involving a box filter to remove streaking artifacts and noise, and a more appropriate regularizer or advanced filter should further improve the reconstruction accuracy.

Acknowledgements

Natural Sciences and Engineering Research Council of Canada, Grant/Award Number 016-05371, the Canadian Institutes of Health Research, Grant Number RN382474-418628, the National MS Society (RG-1507-05301). A.R. is supported by Canada Research Chairs 950-230363. UBC Vancouver is located on the traditional, ancestral, and unceded territory of the Musqueam people.

References

1. Liu, T., Wisnieff, C., Lou, M., Chen, W., Spincemaille, P., & Wang, Y. (2013). Nonlinear formulation of the magnetic field to source relationship for robust quantitative susceptibility mapping. Magnetic resonance in medicine, 69(2), 467-476.

2. Wen, Y., Spincemaille, P., Nguyen, T., Cho, J., Kovanlikaya, I., Anderson, J., ... & Wang, Y. (2021). Multiecho complex total field inversion method (mcTFI) for improved signal modeling in quantitative susceptibility mapping. Magnetic Resonance in Medicine.

3. Milovic, C., Bilgic, B., Zhao, B., Acosta‐Cabronero, J., & Tejos, C. (2018). Fast nonlinear susceptibility inversion with variational regularization. Magnetic resonance in medicine, 80(2), 814-821.

4. QSM Challenge 2.0 Organization Committee, Bilgic, B., Langkammer, C., Marques, J. P., Meineke, J., Milovic, C., & Schweser, F. (2021). QSM reconstruction challenge 2.0: Design and report of results. Magnetic Resonance in Medicine.

5. Marques, J. P., Meineke, J., Milovic, C., Bilgic, B., Chan, K. S., Hedouin, R., ... & Schweser, F. (2021). QSM reconstruction challenge 2.0: A realistic in silico head phantom for MRI data simulation and evaluation of susceptibility mapping procedures. Magnetic resonance in medicine, 86(1), 526-542.

6. Dymerska, B., Eckstein, K., Bachrata, B., Siow, B., Trattnig, S., Shmueli, K., & Robinson, S. D. (2021). Phase unwrapping with a rapid opensource minimum spanning tree algorithm (ROMEO). Magnetic Resonance in Medicine, 85(4), 2294-2308.

Figures

Figure 1. Susceptibility maps computed using the proposed two-pass approach. The second pass is able to recover susceptibility sources which were regularized away during the first pass, but contaminates the susceptibility map with noise and streaking artifacts. The box filter removes the noise but is unable to fully remove the streaking artifacts which propagate into the final susceptibility map.

Figure 2. Comparison of the proposed method with the ground truth susceptibility map. The difference maps show that the first pass is already successful in reconstructing the susceptibility sources and mostly contain streaking artifacts with the only errors confined to veins and the calcification. The second pass corrects the susceptibility values in the veins but is unable to correct the calcification.

Table 1. QSM Reconstruction Challenge 2.0 metrics. Shown are the top 3 NRMSE submissions for each dataset. Bold values indicate the best scores. The proposed method achieves the most Top 3 results for both datasets.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

2461

DOI: https://doi.org/10.58530/2022/2461