2458
The Larmor Frequency of a White Matter Magnetic Microstructure Model with Multiple Sources1Department of Clinical Medicine, Center for Functionally Integrative Neuroscience, Aarhus University, Aarhus, Denmark, 2Medical Physics, Department of Radiology, Faculty of Medicine, University of Freiburg, Freiburg, Germany, 3Champalimaud Research, Champalimaud Centre for the Unknown, Lisbon, Portugal, 4Department of Physics and Astronomy, Aarhus University, Aarhus, Denmark
Synopsis
Mapping tissue magnetic properties with MRI may improve the diagnosis of diseases and enhance our understanding of their basic mechanisms. However, MRI signals are sensitive to both structure and magnetic susceptibility, the so-called “magnetic microstructure”, rendering accurate susceptibility estimation a great challenge. Here, we present an analytical expression for the Larmor frequency of a white matter model of myelinated axons with axially symmetric microscopic susceptibility anisotropy and orientation dispersion. The modelled axons are surrounded by microscopic spherical inclusions with a scalar susceptibility. This goes beyond previous models of white matter magnetic microstructure.
Introduction
Magnetic susceptibility of tissue contains valuable information about chemical composition, enabling noninvasive mapping of de-myelination1, calcification2, iron-dyshomeostasis3. However, accurate estimation of white matter (WM) constituents remains challenging, as myelinated axons exhibit susceptibility tensor character4, are orientationally disperse5, and surrounded by iron-rich tissue6. Previous studies have modelled WM by the so-called generalized mesoscopic Lorentzian tensor7,8, but such approaches were limited to parallel axons and or low volume fractions. Here we relax these restrictions and present an analytical expression for a system with two coexisting types of inclusions; orientationally disperse, myelinated axons, and spherical inclusions. Each axon is modeled by multiple concentric cylinders with axially symmetric microscopic susceptibility anisotropy to mimic myelin layers; the randomly positioned microscopic spherical inclusions with a scalar susceptibility represent iron-rich sources residing outside the cylinders with a scalar susceptibility.Theory
Magnetic microstructureFigure 1 conceptualizes the magnetic microstructure. We model it as a porous medium embedded in an NMR-visible fluid8. The cylinders are infinitely long and randomly positioned (Figure 1A), described by the microscopic indicator function $$$\nu^C(\mathrm{r})$$$. They possess an axially symmetric microscopic susceptibility (Figure 1B),
$$\chi^C=\begin{pmatrix}\chi_\parallel&0&0\\0&\chi_\perp&0\\0&0&\chi_\perp\end{pmatrix}\qquad{(1)}$$
in the lipid eigen-frame ($$$\chi_\parallel$$$ is in the radial direction), and $$$\Delta\chi=\chi_\parallel-\chi_\perp$$$ defines the microscopic susceptibility anisotropy. Cylinders occupy the fraction $$$\zeta^C$$$ of the total volume $$$V$$$. Randomly positioned microscopic spherical inclusions with scalar susceptibility $$$\chi^S$$$ (Figure 1C) reside outside cylinders according to $$$\nu^S(\mathrm{r})$$$ and occupy a volume fraction $$$\zeta^S$$$.
Larmor frequency
When exposing the sample to an external magnetic field $$$\mathbf{B}_0=\mathrm{B}_0\hat{\mathbf{B}}$$$, inclusions become magnetized and induce a magnetic field, perturbing the Larmor frequency of the measured FID signal $$$S(t)$$$. In the fast diffusion regime and in the limit of small signal phase, this perturbation, $$$\Omega=\mathrm{arg}\{S(t)\}/t$$$, becomes
$$\Omega=\gamma{\mathrm{B}_{0}}{{\mathbf{\hat{B}}}^{\text{T}}}\frac{1}{\left(1-\zeta^S-\zeta^C\right)V}\int_Vd\mathbf{r}\left(1-\nu\left(\mathbf{r}\right)\right)\int_{V}{d\mathbf{{r}'}}\mathbf{\Upsilon}\left(\mathbf{r-{r}'}\right)\nu \left({\mathbf{{r}'}}\right)\mathbf{\chi}\left({\mathbf{{r}'}}\right)\mathbf{\hat{B}}.\qquad{(2)}$$
$$$\mathbf{\Upsilon}$$$ is the Lorentz-corrected dipole field9. As explained in previous studies8, and illustrated in Figure 2, $$$\Omega$$$ can be divided into two contributions: a mesoscopic, $$$\Omega^\mathrm{Meso}$$$, and a macroscopic, $$$\Omega^\mathrm{Macro}$$$ one, capturing magnetic field-effects at corresponding length scales, respectively: $$\Omega=\Omega^\mathrm{Meso}+\Omega^\mathrm{Macro}.\qquad{(3)}$$
We find $$$\Omega^\mathrm{Macro}$$$ depends on coarsed magnetic microstructure and overall sample shape
$$\Omega^\mathrm{Macro}=\gamma{\mathrm{B}_{0}}{{\mathbf{\hat{B}}}^{\text{T}}}\mathbf{\Upsilon}^{\mathrm{Macro}}\left(\zeta^C\chi_\perp+\zeta^S\chi^S+\zeta^C\Delta\chi\left(\sum_{m=-2}^2p^{2m}\mathbf{\mathcal{Y}}^{2m}-1\right)\right)\mathbf{\hat{B}},\qquad{(4)}$$
where $$\mathbf{\Upsilon}^{\mathrm{Macro}}=\frac{1}{V}\int_Vd\mathbf{r}\int_Vd\mathbf{r}'\mathbf{\Upsilon}(\mathbf{r}-\mathbf{r}')\qquad{(5)}$$
denotes the sample-averaged dipole tensor, $$$p^{2m}$$$ are $$$l=2$$$ Laplace expansion coefficients of the fiber orientation distribution (fODF), $$$\mathcal{Y}^{2m}$$$ is the $$$l=2$$$ symmetric trace-free tensor representation of SO(3)10. For $$$\Omega^\mathrm{Meso}$$$ we find
$$\Omega^\mathrm{Meso}=-\gamma{\mathrm{B}_{0}}\left(\left(\zeta^C\chi_\perp-\tilde{\zeta}^S\chi^S\right)\sum_{m=-2}^2p^{2m}Y_2^m(\mathbf{\hat{B}})+\Delta\chi\frac{1}{3}\left(\frac{1}{6}\zeta^C-\tilde{\zeta}^C\right)\left(p^{2m}Y_2^m(\mathbf{\hat{B}})-1\right)
\right).\qquad{(6)}$$
$$$\tilde{\zeta}^C$$$ describes intra-cylindrical structure
$$\tilde{\zeta}^C=\frac{1}{1-\zeta^S-\zeta^C}\left(\sum_{m>w}\left(\zeta^C_{R_m}-\zeta^C_{r_m}\right)\mathrm{ln}\left(\frac{R_w}{r_w}\right)-\sum_w\mathrm{ln}\left(\frac{R_w}{r_w}\right)\right).\qquad{(7)}$$
$$$R_m$$$ denotes the radius of the outer layers of the mth shell with volume fraction $$$\zeta^C_{R_m}$$$, while $$$r_m$$$ denotes inner radii of each shell. $$$\tilde{\zeta}^S$$$ is an effective spherical weight defined by
$$\tilde{\zeta}^S=\zeta^S\frac{\zeta^C+\zeta^S\frac{\zeta^{EC}}{1-\zeta^{EC}}}{1-\zeta^S-\zeta^C},\qquad{(8)}$$
where $$$\zeta^{EC}$$$ denotes extra-cylindrical volume fraction.
Methods
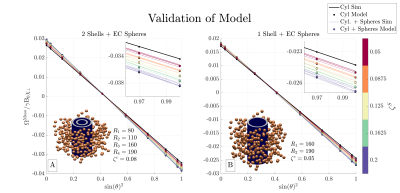
ValidationWe performed computer simulations to validate $$$\Omega^\mathrm{Meso}$$$ (Eq. (6)). $$$\Omega^\mathrm{Meso}$$$ was validated previously11 when $$$\Delta\chi=\chi^S=0$$$ in the presence of orientation dispersion. Here we limit the validation to consider a multi-layer cylinder surrounded by spherical inclusions (full description can be found in Figure 3) as a comprehensive numerical validation is ongoing.
Predicted Larmor frequency
We considered the predicted behavior of $$$\Omega^\mathrm{Meso}$$$ for cylinders with axially symmetric orientation dispersion surrounded by spherical inclusions (a full description can be found in Figure 4). We varied 1) Orientation dispersion from parallel to uniformly oriented; 2) susceptibility anisotropy; and 3) sphere susceptibility.
Results
Figure 3 shows simulations validating $$$\Omega^\mathrm{Meso}$$$, while Figure 4 demonstrates the predicted behavior of $$$\Omega^\mathrm{Meso}$$$. Its overall functional behavior is $$$A\cdot\sin(\theta)^2+B$$$, where $$$\theta$$$ is the angle between the mean cylinder axis and external field $$$\mathbf{\hat{B}}$$$. We find orientation dispersion dampens $$$\Omega^\mathrm{Meso}$$$ variation, while $$$\Delta\chi$$$ produces a non-zero $$$\Omega^\mathrm{Meso}$$$ (approx -0.1 of $$$\gamma\mathrm{B}_0\chi_\perp$$$ for this microstructure) for maximal dispersion and changes the zero-crossing away from the magic angle. Spherical inclusions produce a small contribution that depends on the model fODF. This stems from the correlation in the sphere positions induced by the presence of cylinders via the restriction of no overlap.Discussion
Equations (6)-(8) reveal the behavior of $$$\Omega^\mathrm{Meso}$$$ for a WM model consisting of long cylinders and spherical inclusions. $$$\Omega^\mathrm{Meso}$$$ depends on volume-weighted susceptibility parameters describing the average magnetic response for each inclusion-type, while their orientation is captured by $$$p^{2m}$$$ of the fODF. Estimating $$$p^{2m}$$$ from diffusion MRI (dMRI), removes 5 structural parameters, which leaves only 3 undermined susceptibilities. Resolving all parameters would thus require measuring $$$\Omega$$$ at multiple orientations or exploiting additional information from other contrasts or modalities. The functional behavior of $$$\Omega^\mathrm{Meso}$$$ (c.f. figure 4) agrees with recent findings12 for the mesoscopic frequency from WM axons, and generalizes the mesoscopic Lorentzian tensor7,8 for this microstructure.Limitations
Our model is a simplification of real WM microstructure, where axons exhibit axonal caliber-variation, undulation13, and inclusions in all water compartments. However, it captures important microstructural features that have not been accounted for previously, as current models assume parallel cylinders and low volume fraction. Furthermore, our model can easily be extended to include e.g., myelin-basic proteins, phospholipid-proteins within the lipids and cylindrical inclusions such as unmyelinated axons, neurofilaments and microtubules.
Conclusion
We presented an expression for the Larmor frequency of a WM model consisting of multi-layer cylinders, with orientation dispersion and susceptibility anisotropy, surrounded by spherical inclusions with isotropic susceptibility. This goes beyond previous models7,8 and relates orientation dependence to the fODF, measurable with dMRI11,14-16. We believe this result brings susceptibility MRI one step closer to becoming a useful tool in clinical research.Acknowledgements
This study is funded by the Independent Research Fund (grant 8020-00158B), Denmark, and by Helga & Peter Korning's Foundation.References
1. Love S. Demyelinating diseases. J Clin Pathol. 2006;59(11):1151-1159. doi:10.1136/jcp.2005.031195
2. Grech R, Grech S, Mizzi A. Intracranial calcifications: A pictorial review. Neuroradiol J. 2012;25(4):427-451. doi:10.1177/197140091202500406
3. Ndayisaba A, Kaindlstorfer C, Wenning GK. Iron in neurodegeneration - Cause or consequence? Front Neurosci. 2019;13:180. doi:10.3389/fnins.2019.00180
4. Van Gelderen P, Mandelkow H, De Zwart JA, Duyn JH. A torque balance measurement of anisotropy of the magnetic susceptibility in white matter. Magn Reson Med. 2015;74(5):1388-1396. doi:10.1002/mrm.25524
5. Ronen I, Budde M, Ercan E, Annese J, Techawiboonwong A, Webb A. Microstructural organization of axons in the human corpus callosum quantified by diffusion-weighted magnetic resonance spectroscopy of N-acetylaspartate and post-mortem histology. Brain Struct Funct. 2014;219(5):1773-1785. doi:10.1007/s00429-013-0600-0
6. Fukunaga M, Li TQ, Van Gelderen P, et al. Layer-specific variation of iron content in cerebral cortex as a source of MRI contrast. Proc Natl Acad Sci U S A. 2010;107(8):3834-3839. doi:10.1073/pnas.0911177107
7. Yablonskiy DA, Sukstanskii AL. Generalized Lorentzian Tensor Approach (GLTA) as a biophysical background for quantitative susceptibility mapping. Magn Reson Med. 2015;73(2):757-764. doi:10.1002/mrm.25538
8. Kiselev VG. Larmor frequency in heterogeneous media. J Magn Reson. 2019;299:168-175. doi:10.1016/j.jmr.2018.12.008
9. Ruh A, Kiselev VG. Calculation of Larmor precession frequency in magnetically heterogeneous media. Concepts Magn Reson Part A. 2018;47A(1):e21472. doi:10.1002/cmr.a.21472
10. Thorne KS. Multipole expansions of gravitational radiation. Rev Mod Phys. 1980;52(2):299-339. doi:10.1103/RevModPhys.52.299
11. Sandgaard A, Kiselev VG, Shemesh N, Jespersen SN. Rotation-Free Mapping of Magnetic Tissue Properties in White Matter. ISMRM 2021.
12. Wharton S, Bowtell R. Effects of white matter microstructure on phase and susceptibility maps. Magn Reson Med. 2015;73(3):1258-1269. doi:10.1002/mrm.25189
13. Andersson M, Kjer HM, Rafael-Patino J, et al. Axon morphology is modulated by the local environment and impacts the noninvasive investigation of its structure–function relationship. Proc Natl Acad Sci U S A. 2021;117(52):33649-33659. doi:10.1073/PNAS.2012533117
14. Novikov DS, Fieremans E, Jespersen SN, Kiselev VG. Quantifying brain microstructure with diffusion MRI: Theory and parameter estimation. NMR Biomed. 2019;32(4):e3998. doi:10.1002/nbm.3998
15. Jensen JH, Russell Glenn G, Helpern JA. Fiber ball imaging. Neuroimage. 2016;124(Pt A):824-833. doi:10.1016/j.neuroimage.2015.09.049
16. Jeurissen B, Tournier JD, Dhollander T, Connelly A, Sijbers J. Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data. Neuroimage. 2014;103:411-426. doi:10.1016/j.neuroimage.2014.07.061
17. Yablonskiy DA, Haacke EM. Theory of NMR signal behavior in magnetically inhomogeneous tissues: The static dephasing regime. Magn Reson Med. 1994;32(6):749-763. doi:10.1002/mrm.1910320610
Figures


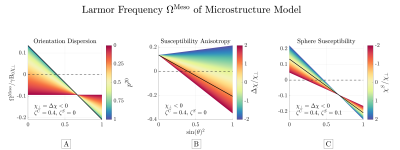
Predicted $$$\Omega^\mathrm{Meso}$$$ as function of B-field orientation for cylinders with axially
symmetric orientation dispersion consisting of 1 shell. The frequency is linear with $$$\sin(\theta)^2$$$, where
$$$\theta$$$ is angle between mean cylinder axis and external field. A: dispersion dampens variations while focal point remains at the magic angle, where the orientation dependent contribution is zero. B: anisotropy scales and shifts the zero-crossing. C: spheres scales the frequency. The solid black line (-)
indicates identical settings across all panels.