Introduction

White matter tissue microstructure anisotropy has been shown to imprint itself on a variety of observables in quantitative MRI. The observation that quantitative parameters acquired with MRI can be anisotropic is central to diffusion tensor imaging (DTI).¹ In the brain, DTI exploits the fact that the anisotropy of white matter results in enhanced diffusion along the length of the axon compared to the restricted diffusion along radial directions. This effect can be used to approximate the local fiber orientation as the principal direction of diffusion.¹ More recently both the $$$R_2$$$ and $$$R_2^*$$$ transverse relaxation rates have also been shown to depend on the orientation of anisotropic tissue to the magnetic field of the scanner. ^2-6 Relaxation rates increase when the axon is oriented perpendicular to the magnetic field due to the presence of mesoscopic field inhomogeneities. These field inhomogeneities are created by the interaction between the main magnetic field and susceptibility sources such as diamagnetic myelin.^7,8 Simulations of a simple model system of white matter have shown that the mean diffusivity (MD) obtained with DTI are also expected to depend on orientation.⁷ In this abstract we present an analysis of the orientation dependence of the mean, axial (AD) and radial (RD) diffusivities in DTI.

Methods

Eight healthy adult subjects (mean age$$$=21\pm2$$$ years, 6 females) were scanned at 3T. Fiber orientation was mapped with DTI ($$$T_R=7,015\,\text{ms}$$$, $$$T_E=60\,\text{ms}$$$, $$$\text{flip angle}=90^{\circ}$$$, $$$\text{b-factor}=700\,\text{mm}^3\text{/s}$$$, $$$\text{number of directions}=60$$$, $$$\text{acquisition matrix}=100 \times 99$$$, $$$\text{number of slices}=70$$$, reconstructed voxel size$$$=2\times 2\times2.2\,\text{mm}^3$$$). DTI data were analyzed using FSL DTIFIT. White matter masks were created using FSL FAST on $$$T_1$$$-weighted images and registered to the DTI space using FSL FLIRT. Voxels were pooled across the whole white matter according to the angle between the main magnetic field of the scanner and the principal diffusion direction in $$$5^{\circ}$$$ intervals. MD, AD, and RD were plotted as a function of the local fiber orientation angle. A model of diffusion-mediated dephasing was fit to the data.

Results

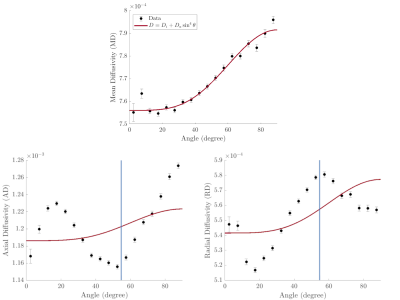
Figure 1 shows the diffusion parameters MD, RD, and AD as a function of fiber angle $$$\theta$$$. All diffusivities show an increase at $$$90^{\circ}$$$ compared to $$$0^{\circ}$$$. MD shows a monotonic increase with fiber angle and is well fit by the model of diffusion-mediated dephasing yielding an adjusted $$$\chi^2=0.97$$$. AD and RD show a markedly different orientation dependence and are not well fit by the model with an adjusted $$$\chi^2=0.09$$$ and $$$\chi^2=0.32$$$ respectively. Most notably, the AD has a minimum and the RD a maximum located close to the so-called magic angle of $$$54.7^{\circ}$$$ indicated by the vertical blue line.

Discussion

The orientation dependence observed in MD agrees well with predictions from simulations by Knight et al.⁷ showing an increase in MD for higher angles. At perpendicular orientation the interactions between the diamagnetic myelin and the main magnetic field create field gradients that add to the applied diffusion gradient and result in an increase in the apparent diffusivity. This is well fit by the model of diffusion through field inhomogeneities that describes orientation dependence in $$$R_2$$$. A minimum in diffusivity at the magic angle may be explained by the presence of a bound water pool of structured water that has low diffusivity and high $$$R_2$$$. At the magic angle dipole-dipole interaction between the water molecules is minimized and $$$R_2$$$ is reduced such that its signal may become visible.⁹ This would increase the total signal, but reduce the fraction of signal with low diffusivity. While this may provide a tentative explanation for our findings in AD, the opposite effect is seen in RD. In a future study we plan to acquire DTI and NODDI data at different head orientations which will allow us to study the effect of orientation dependence in diffusion imaging in more detail.¹⁰ In this analysis both fiber orientation and diffusivities were obtained from the same DTI scan. Varying the head orientation will allow for an independent orientation measure. This will also enable us to assess the influence of anatomical features on the first few bins that contain only very few voxels. Simulations have shown that crossing fibers affect orientation dependency.⁷ Multi-shell diffusion imaging approaches such as NODDI will allow us to probe crossing fibers and better understand how they are reflected in the orientation dependence.

Conclusion

Diffusion metrics obtained with DTI show orientation dependence in adult human white matter. While orientation dependence in MD is well described by a model of diffusion through field inhomogeneities, the orientation dependence of AD and RD tentatively suggest effects of ordered water in the mature human white matter. Future studies of DTI and NODDI at different head orientations are expected to further improve our understanding of the effect of orientation dependence on diffusion imaging. Correcting for orientation dependence has the potential to enhance the sensitivity of diffusion metrics to pathological tissue changes of clinical interest.

Acknowledgements

UBC Vancouver is located on the traditional, ancestral, and unceded territory of the Musqueam people.
This research is supported by the Natural Sciences and Engineering Research Council of Canada, Grant/Award Number 016-05371, the Canadian Institutes of Health Research, GrantNumber RN382474-418628, the National MS Society (RG-1507-05301). A.R. is supported by Canada Research Chairs 950-230363. L.B. is supported by a scholarship from the German National Academic Foundation (Studienstiftung des Deutschen Volkes).

References

[1] L. J. O’Donnell and C.-F. Westin, “An introduction to diffusion tensor image analysis”, Neurosurg. Clin. N. Am., vol 22, pp. 185-viii, Apr. 2011, doi: 10.1016/j.nec.2010.12.004.
[2] S. Wharton and R. Bowtell, “Fiber orientation-dependent white matter contrast in gradient echo MRI”, PNAS, vol. 109, pp.18559-18564, Nov. 2012, doi: https://doi.org/10.1073/pnas.1211075109.
[3] S.-H. Oh, Y.-B. Kim, Z.-H. Cho, and J. Lee, “Origin of B0 orientation dependent R2* (=1/T2*) in white matter,” NeuroImage, vol. 73, pp. 71–79, Jun. 2013, doi: 10.1016/j.neuroimage.2013.01.051.
[4] M. J. Knight, B. Wood, E. Couthard, and R. Kauppinen, “Anisotropy of spin-echo T2 relaxation by magnetic resonance imaging in the human brain in vivo,” Biomed. Spectrosc. Imaging, vol. 4, no. 3, pp. 299–310, Jan. 2015, doi: 10.3233/BSI-150114.
[5] C. Birkl, J. Doucette, M. Fan, E. Hernández‐Torres, and A. Rauscher, “Myelin water imaging depends on white matter fiber orientation in the human brain,” Magn. Reson. Med., vol. 85, no. 4, pp. 2221–2231, 2021, doi: https://doi.org/10.1002/mrm.28543.
[6] C. M. W. Tax, E. Kleban, M. Chamberland, M. Baraković, U. Rudrapatna, and D. K. Jones, “Measuring compartmental T2-orientational dependence in human brain white matter using a tiltable RF coil and diffusion-T2 correlation MRI,” NeuroImage, vol. 236, p. 117967, Aug. 2021, doi: 10.1016/j.neuroimage.2021.117967.
[7] M. J. Knight, S. Dillon, L. Jarutyte, and R. A. Kauppinen, “Magnetic Resonance Relaxation Anisotropy: Physical Principles and Uses in Microstructure Imaging,” Biophys. J., vol. 112, no. 7, pp. 1517–1528, Apr. 2017, doi: 10.1016/j.bpj.2017.02.026.
[8] M. J. Knight and R. A. Kauppinen, “Diffusion-mediated nuclear spin phase decoherence in cylindrically porous materials,” J. Magn. Reson., vol. 269, pp. 1–12, Aug. 2016, doi: 10.1016/j.jmr.2016.05.007.
[9] M. Bydder, A. Rahal, G.D. Fullerton, and G.M. Bydder, “The magic angle effect: A source of artifact, determinant of image contrast, and technique for imaging”, J. Magn. Reson., vol. 25, pp. 290-300, 2007, doi: https://doi.org/10.1002/jmri.20850
[10] H. Zhang, T. Schneider, C. A. Wheeler-Kingshott, and D. C. Alexander, “NODDI: Practical in vivo neurite orientation dispersion and density imaging of the human brain“, NeuroImage, vol. 61, pp. 1000-1016, Mar. 2012, doi: 10.1016/j.neuroimage.2012.03.072.