2451
Prospects of non-Cartesian 3D-SPARKLING encoding for functional MRI: A preliminary case study for retinotopic mapping1Université Paris-Saclay, CEA, Neurospin, CNRS, Gif-sur-Yvette, France, 2Université Paris-Saclay, Inria, Parietal, Palaiseau, France, 3Siemens Healthcare SAS, Saint-Denis, France
Synopsis
For the first time, non-Cartesian 3D-SPARKLING (Spreading Projection Algorithm for Rapid K-space sampLING) encoding scheme was used for task-based fMRI (retinotopic mapping) at 7T. Additionally, this new acquisition technique was compared with 3D-EPI, considered as one of the reference acquisition schemes in high-resolution fMRI. The experiment was performed on a single participant at 1mm isotropic and for a temporal resolution of 2.4s. We found that both techniques yield similar statistically significant activation patterns in the visual cortex.
Introduction
In BOLD fMRI, higher spatio-temporal resolution is key for an improved spatial (sensitivity/specificity trade-off) and temporal (haemodynamic response) characterization of task-related brain activity. Parallel imaging1–3, accelerated MRI techniques and higher magnetic fields participated in enhancing the resolution4–6 in fMRI. However, state-of-the-art Cartesian encoding schemes, such as Segmented 3D-EPI7 and 2D SMS-EPI8, remain sub-optimal in terms of sampling efficiency (broader k-space coverage in a given amount of time) in the whole brain imaging setting. In contrast, non-Cartesian readouts, such as spiral imaging9,10, have gained popularity thanks to their higher sampling efficiency, hence their shorter acquisition times and improved spatio-temporal resolution. Recently, non-Cartesian SPARKLING encoding scheme was developed, first for 2D11 then 3D12,13 anatomical MRI. 3D-SPARKLING13 generates multi-shot sampling patterns in accordance with compressed sensing theories14. These patterns follow a prescribed target sampling density while meeting the hardware constraints (maximum gradient and slew rate). Higher acceleration factors can be achieved with 3D-SPARKLING by minimizing the number of shots and homogenizing full k-space coverage. As these properties are instrumental in reaching high resolution in fMRI, we investigated how to extend 3D-SPARKLING to fMRI and compared it to state-of-the-art CAIPIRINHA16 segmented 3D-EPI for whole brain fMRI at 7T and 1mm3.Methods
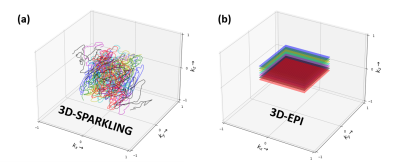
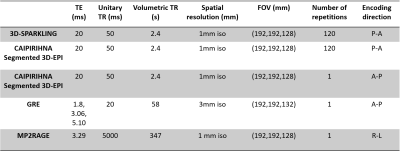
A single healthy volunteer was scanned with a Siemens Magnetom 7T and a 1Tx-32Rx Nova head coil. Task-based fMRI data was collected along two consecutive runs that implemented a classic retinotopic mapping paradigm with a rotating wedge (clockwise and anti-clockwise) with a period of 32s. The code of the experimental paradigm is available in17. FMRI data was acquired with 3D-SPARKLING (Fig.1-a) and CAIPIRINHA segmented 3D-EPI (Fig.1-b), for the same sequence parameters, a total acquisition time of 4min and 48s for each run and two runs per sequence. The acquisition parameters are reported in Fig.2. A 15s calibration was run once at the start of each EPI sequence (be it single or multiple-repetition). A gradient recalled echo (GRE) sequence with three echoes was used (once during the session) to acquire both a $$$B_{0}$$$ map and external sensitivity maps for 3D-SPARKLING data. Raw data of the first echo from the GRE sequence was used to compute the sensitivity maps whereas the full dataset (3 echoes) was used to obtain an accurate estimate of the $$$B_{0}$$$ map. The $$$B_{0}$$$ and sensitivity maps were extrapolated to fit the spatial resolution and field-of-view of the 3D-SPARKLING fMRI scans. An anatomical T1w scan was acquired through an MP2RAGE sequence. Details of the sequences are given in Fig.2.Each scan based on 3D-SPARKLING data was reconstructed independently using an externally calibrated multi-coil compressed sensing reconstruction algorithm15 and the above mentioned sensitivity maps. This reconstruction method involves a sparsity promoting prior $$$\ell_1$$$-norm in the wavelet domain (Symlet-8) and the Proximal Optimized Gradient Method (POGM) algorithm18. This approach is implemented in the pysap-mri plugin19 of the pySAP package20. Moreover, static $$$\Delta B_{0}$$$ was corrected during the reconstruction phase by including the acquired $$$B_{0}$$$ map in the definition of the extended Fourier operator following the approach proposed in21. The 3D-EPI data was reconstructed with a GRAPPA-based reconstruction and corrected for $$$B_{0}$$$ distortions using the TOPUP mechanism that relied on an additional single-repetition A-P (Fig.2) acquisition22. Minimum preprocessing was applied to 3D-SPARKLING and 3D-EPI time-series: Motion correction was done with FSL22. Anatomo-functional coregistration was straightforward as the acquired scans share the same spatial resolution and field-of-view (Fig.2). No co-registration in a standard space template was applied as we consider single participant data. No spatial smoothing was applied to preserve the advantages of the native 1mm isotropic resolution. Retinotopic data was analyzed using a two-session first-level GLM that includes 2 paradigm-related regressors (parametric, continuous and sinusoidal), 6 motion regressors, a drift regressor and the baseline. A statistical test over the two sinusoidal regressors was used and the entire brain was thresholded at $$$p<0.001$$$ (uncorrected for multiple comparisons). The implementation was done through the Nilearn package23. The comparison was performed after the statistical analysis of the functional data: Visually and according to the z-score values and distributions.
Results and Discussion
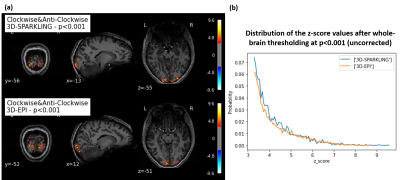
Fig.3-a shows that, for both techniques, we found similar activation patterns in the visual cortex. However, the activations seem more significant for 3D-SPARKLING. Fig.3-b confirms the visually-observed similarity and the higher significance of 3D-SPARKLING activations (maximum z-score value). In Fig.4, we observe larger spatial extent of activation clusters for 3D-SPARKLING in comparison to 3D-EPI. Interestingly, activation patterns in both cases seem to closely fit the cortical surface. This indicates good spatial specificity for both techniques. Taking into account the fact that we consider single participant data, a more advanced statistical comparison can not be done. For this purpose, data from different individuals needs to be further collected. The two techniques need to be compared for different spatio-temporal resolutions as well. As of now, we can conclude that activation patterns are similar for the two techniques.Conclusion
3D-SPARKLING encoding has a real potential for fMRI applications. With all shots crossing the center of k-space, 3D-SPARKLING encoding opens up possibilities towards variable spatio-temporal resolution setups. It can also be extended to generate full-4D sampling patterns along with low rank and sparse reconstruction methods.Acknowledgements
We thank Benedict A. Poser for equipping us with the 3D-EPI sequence. We thank Alexis Amadon for his code for $$$B_{0}$$$ map computation as well. Leducq Foundation (Large Equipement ERPT program, NEUROVASC7T project) provided financial support for this work. Chaithya G R was supported by the CEA NUMERICS program, which has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant agreement No 800945.References
1 J. Hamilton. Recent Advances in Parallel Imaging for MRI. Progress in Nuclear Magnetic Resonance Spectroscopy, 101:71–95, 2017.
2 A . Deshmane et al. Parallel MI Imaging. Journal of Magnetic Resonance Imaging, 36(1):55–72, 2012.
3 Klaas P Pruessmann. Encoding and Reconstruction in Parallel MRI. NMR in Biomedicine, 19(3):288–99, 2006.
4 A. Thanh Vu et al. Tradeoffs in Pushing the Spatial Resolution of fMRI for the 7T Human Connectome Project. Neuroimage, 154:23–32, 2017.
5 O. Viessmann et al. High-resolution fMRI at 7 Tesla: Challenges, Promises and Recent Developments for Individual-focused fMRI Studies. Current Opinion in Behavioral Science, 40:96–104, 2021.
6 R. M. Heidemann et al. Isotropic Submillimeter fMRI in the Human Brain at 7T: Combining Reduced Field-of-view and Partially Parallel Acquisitions. Magnetic Resonance in Medicine, 68(5):1506–16, 2012.
7 B.A. Poser et al. Three Dimensional Echo-planar Imaging at 7 Tesla. Neuroimage, 51(1):261–6, 2010.
8 C. Le Ster et al. Comparison of SMS-EPI and 3D-EPI at 7T in an fMRI Localizer Study with Matched Spatiotemporal Resolution and Homogenized Excitation Profiles. PLOS ONE, 14(11), 2019.
9 B. Riemenschneider et al. Trading off Spatio-temporal Properties in 3D High Speed fMRI Using Interleaved Stack-of-spirals Trajectories. Magnetic Resonance in Medicine, 86(2):777–790, 2021.
10 G. H. Glover. Spiral Imaging in fMRI. Neuroimagee, 62(2):706–12, 2012.
11 C. Lazarus et al. SPARKLING: Variable-density k-space Filling Curves for Accelerated T2*-weighted MRI. Magnetic Resonance in Medicine, 81(6):3643–3661, 2019.
12 C. Lazarus et al. 3D Variable-density SPARKLING Trajectories for High-resolution T2*-weighted Magnetic Resonance Imaging. NMR in Biomedicine, 33(9), 2020.
13 G.R. Chaithya et al. Optimizing Full 3D SPARKLING Trajectories for High Tesolution T2*-weighted Magnetic Resonance Imaging. under review at IEEE Transactions on Medical Imaging, 2021.
14 M. Lustig et al. Compressed Sensing MRI. IEEE Signal Processing Magazine, 25(2):72–82, 2008.
15 L. El Gueddari et al. Self-calibrating Nonlinear Reconstruction Algorithms for Variable Density Sampling and Parallel Reception MRI. IEEE 10th Sensor Array and Multichannel Signal Processing Workshop (SAM), 2018.
16 F. A. Breuer et al. Controlled Aliasing in Parallel Imaging Results in Higher Acceleration (CAIPIRINHA) for Multi-slice Imaging. Magnetic Resonance in Medicine, 53(3):684–91, 2005.
17 https://github.com/hbp-brain-charting/public_protocols.
18 P. L. Combettes et al. Proximal Splitting Methods in Signal Processing. FixedPoint Algorithms for Inverse Problems in Science and Engineering, pages 185–212, 2011.
19 https://github.com/CEA_COSMIC/pysap-mri.
20 S. Farrens et al. Pysap: Python Sparse Data Analysis Package for Multidisciplinary Image Processing. Astronomy and Computing, 32, 2020.
21 J. A. Fessler et al. Toeplitz-based Iterative Image Reconstruction for MRI with Correction for Magnetic Field Inhomogeneity. IEEE Transactions On Signal Processing, 53(9):3393–3402, 2005.
22 https://fsl.fmrib.ox.ac.uk/fsl/fslwiki.
23 https://nilearn.github.io/stable/index.html.
Figures