2370
COSMOS-Based Susceptibility Estimations: Accuracy Assessment and Comparisons of QSM and Multiple-Angle Acquisitions1Max Planck Institute for Human Cognitive and Brain Sciences, Leipzig, Germany, 2Max Planck Institute for Evolutionary Anthropology, Leipzig, Germany, 3Tai Chimpanzee Project, Centre Suisse de Recherches Scientifiques en Cote d'Ivoire, Abidjan, Cote D'ivoire
Synopsis
Calculation Of Susceptibility through Multiple Orientation Sampling (COSMOS) is assessed comparing the optimal, a clinically feasible and multiple-orientation schemes. The optimal COSMOS estimation is used as a gold standard and is compared to the other schemes using the similarity index (SSIM), mean absolute error (MAE) and Pearson’s coefficient (PC). Further comparisons include Thresholded K-space Division (TKD) quantitative susceptibility mapping. For selected white-matter regions, linear regression is used to assess the similarities between the different estimations.
Introduction
Brain pathologies are often linked to local alterations of iron or myelin, making their quantitation highly important. Multiple methods have been proposed for this purpose, including Quantitative Susceptibility Mapping (QSM)1,2. There are two major problems with single-orientation QSM: (i) inversion from local tissue phase to susceptibility is intrinsically ill-posed; (ii) anisotropy of magnetic susceptibility in brain tissue is typically ignored3.Most QSM applications employ post-acquisition solutions to the first problem, with Thresholded K-space Division (TKD)4 being a prominent example. Regarding acquisition-based approaches, Calculation Of Susceptibility through Multiple Orientation Sampling (COSMOS) has been introduced, which requires sampling at three or more orientations of the object inside the magnetic field. 3 An estimation of the optimal scheme suggests rotations by 0°, 60° and 120° about the (physical) x- or y-axes. This selection is believed to yield excellent susceptibility estimates by fully addressing the ill-posed inversion problem and, additionally, partially addressing the anisotropy problem. However, the feasibility of COSMOS in in-vivo human brain imaging is challenging because achievable head rotations are limited to a small range of ±20°, which deviates substantially from the ideal rotation scheme. In the current study, we compared the optimal COSMOS scheme to one that considers constraints under in vivo conditions as well as to TKD-QSM. Acquisitions using more than 3 orientations (4 to 10) were also included to evaluate the potential impact from additional orientation information in susceptibility estimations.
Methods
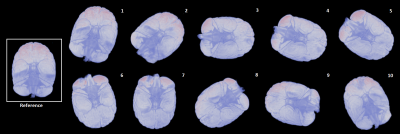
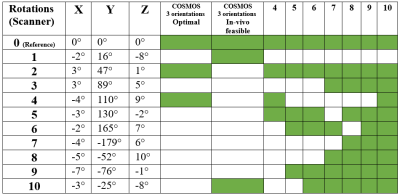
Complex 3D multi-echo GRE data (1mm isotropic nominal resolution) were acquired with a 32-channel headcoil on a 3T MAGNETOM Skyra Connectom (Siemens, Erlangen Germany) in fixed chimpanzee brain. The animal had died from natural causes in Tai National Park, Ivory Coast. The brain was immersed in Fomblin and positioned in a 3D-printed container adapted to its individual anatomy. Acquisitions at TE=30 ms and a subset of 11 reorientations of the specimen within the main magnetic field from a total dataset comprising 60 evenly distributed independent orientations were used for the current study. ESPIRiT-SVD was used for coil combination.5,6Multi-orientation phase volumes were registered to a reference employing transformations that were derived by registering the corresponding magnitude volumes using FSL7. The 11 phase volumes used in different combinations were selected to ensure significant rotation (>15°) about the (physical) y-axis, whereas rotations about the remaining axes always remained below 10° (Figure 1).
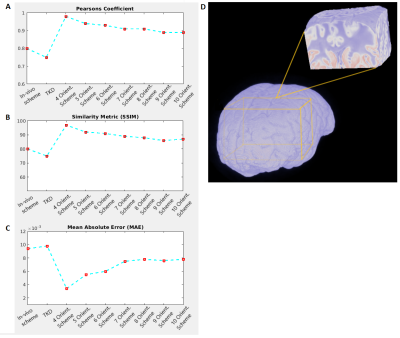
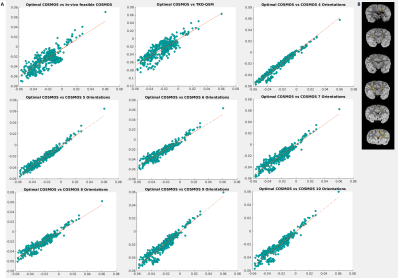
Laplacian phase unwrapping and background-phase removal using V-SHARP8 were performed on the selected registered phase volumes. All further image processing routines were implemented in Matlab comprising the COSMOS model, the TKD-QSM estimate, and the statistical analysis pipelines, which included the 3D-Similarity Index (SSIM), Mean Absolute Error (MAE) and Pearson’s Coefficient (PC) performed on a large region of interest (ROI) with combined gray matter (GM) and white matter (WM) (Figure 4B) as well as linear regression in selected WM ROIs (Figure 5B).
Results
Fixed brain specimens permit arbitrary rotations to overcome restrictions of in vivo experiments. The availability of a chimpanzee brain further supported more efficient high-resolution acquisitions compared to a human brain while still showing a complex WM architecture.Visual inspection of the susceptibility maps obtained with optimal COSMOS, in vivo-feasible COSMOS and TKD-QSM (Figure 3A) indicate differences in WM and GM regions. The high-angular COSMOS implementations (4 to 10 orientations; Figure 3B) exhibit higher resemblance to the optimal-scheme results when limiting the number of orientations (4 and 5).
The visual observations are corroborated by the different comparison metrics PC, SSIM and MAE. Using the optimal 3-orientation COSMOS scheme as reference, the 4-orientation COSMOS estimates indicate the smallest error in addition to higher PC and SSIM values, while higher angular-resolution schemes yielded slightly increased error and decreased PC/SSIM until a plateau was reached around 8 orientations. TKD-QSM yielded the highest errors and lowest PC and SSIM. However, its accuracy was still is comparable to the in vivo-feasible COSMOS scheme (Figure 4A).
In exemplarily selected WM ROIs, linear regression of the optimal COSMOS susceptibility estimates with TKD-QSM and the in vivo-feasible COSMOS results indicate similar dispersion (Figure 5), validating the other statistical comparisons. Higher angular-resolution COSMOS schemes in the same WM ROIs also followed the trend observed in the general statistical comparisons, with 4- and 5-orientation schemes indicating the least dispersion. Again, with more than 5 orientations, the dispersion increased without significant differences in the estimations beyond 7 orientations.
Discussion
Our results indicate limitations of the COSMOS model in in-vivo applications, which only slightly outperforms single-orientation TKD-QSM, when both are compared to the optimal COSMOS reference scheme. Considering the added complexity of COSMOS acquisitions and registration, this challenges the suitability of the model, which has been used as gold standard in comparisons of QSM pipelines.9 Our results further indicate that the theoretical minimum of 3 orientations (rotations with 60° increments) that is required to stabilize the inverse problem, is already the optimal choice, whereas sets of more orientations with smaller angle increments did not achieve significant improvements. This is probably due to an accumulation of registration errors. We note that even the optimal COSMOS scheme for estimating susceptibility can induce bias as it does not consider internal anisotropy of the magnetic susceptibility, in particular in WM.Acknowledgements
This work was funded by the EU through the ITN “INSPiRE-MED” (H2020-MSCA-ITN-2018, #813120).
We are grateful to the Evolution of Brain Connectivity (EBC) project, the Ministère de l’Enseignement Supérieur et de la Recherche Scientifique, the Ministère de Eaux et Fôrests in Côte d’Ivoire, and the Office Ivoirien des Parcs et Réserves for permitting the study, and to the staff of the Taï Chimpanzee Project.
References
1. Möller HE, Bossoni L, Connor JR, et al. Iron, myelin, and the brain: Neuroimaging meets neurobiology. Trends Neurosci. 2019; 42: 384-401.
2. Deistung A, Schweser F, Reichenbach JR. Overview of quantitative susceptibility mapping. NMR Biomed. 2017; 30: e3569.
3. Liu T, Spincemaille P, de Rochefort L, et al. Calculation of susceptibility through multiple orientation sampling (COSMOS): A method for conditioning the inverse problem from measured magnetic field map to susceptibility source image in MRI. Magn Reson Med. 2009; 61: 196-204.
4. Wharton S, Schäfer A, Bowtell R. Susceptibility mapping in the human brain using threshold-based k-space division. Magn Res Med. 2010; 63: 1292-1304.
5. Uecker M, Lustig M. Estimating absolute-phase maps using ESPIRiT and virtual conjugate coils. Magn Reson Med. 2017; 77: 1201-1207.
6. Bilgic B, Polimeni JR, Wald LL, et al. Automated tissue phase and QSM estimation from multichannel data. Proceedings of the 24th Annual Meeting of ISMRM. Singapore 2016; 2849.
7. Jenkinson M, Beckmann CF, Behrens TE, et al. FSL. NeuroImage. 2012; 62: 782-790.
8. Özbay PS, Deistung A, Feng X, et al. A comprehensive numerical analysis of background phase correction with V-SHARP. NMR Biomed. 2017; 30: e3550.
9. Langkammer C, Schweser F, Shmueli K, et al. Quantitative susceptibility mapping: Report from the 2016 reconstruction challenge. Magn Reson Med. 2018; 79: 1661-1673.
Figures