INTRODUCTION

Quantitative Susceptibility Mapping (QSM) solves an ill-posed inverse problem, where tissue susceptibilities are derived from the phase of gradient-echo acquisitions¹. Since this is a complex process prone to errors and artifacts, numerous QSM algorithms have been proposed. To compare the performance of these algorithms, two QSM Reconstruction Challenges have been organized (2016, announced in Graz, Austria: RC1², and 2019, announced in Seoul, Korea: RC2^3,4). The Structural Similarity Index Metric (SSIM)^5,6 was first used in the RC1 as an alternative to the Root Mean Squared Error (RMSE) to measure the quality of the QSM reconstructions. As it is based on a perceptual cost, SSIM should reflect the human visual perception of QSM reconstruction quality more closely than RMSE. Optimizing SSIM tended to produce sharper susceptibility maps than using RMSE². However, concerns were raised about the validity of this metric for QSM since maps with obvious artifacts achieved higher SSIM scores than artifact-free solutions. Here, we present the Susceptibility Similarity Index Metric (XSIM): a robust implementation of the SSIM metric specifically tuned for QSM, that avoids these problems.

METHODS

SSIM produces values between 0 and 1, with 1 indicating an image identical to the ground truth. It is defined as the pixel-wise multiplication of three loss functions (luminance, variance, and structural), simplified as follows^5,6:
$$SSIM(x,y)=\sum_{ROI}\frac{(2μ_xμ_y+c_1)(2σ_{xy}+c_2)}{(μ_x^2+μ_y^2+c_1)(σ_x^2+σ_y^2+c_2)}$$
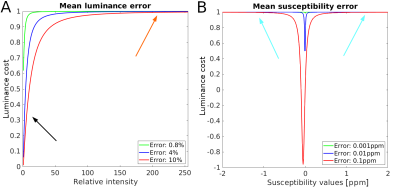
where x and y are the two images being compared inside 3x3x3 moving windows, μ is the window mean value, σ² the window variance, and σ_xy the covariance between corresponding windows. Parameters c₁ and c₂ are used to stabilize the cost functions: large values make the functions insensitive to errors, whereas small values may lead to excessive sensitivity to noise. Typically, these parameters are defined as: $$$c_i = K_iL$$$ with standard values $$$K_1=0.01$$$, $$$K_2=0.03$$$, and $$$L=255$$$. The implementation of SSIM for RC1² required rescaling QSM images to range between 0 and 255 and was evaluated using default parameters. As shown in Figure 1A, this results in a bias that over-penalizes errors in the diamagnetic range, whereas paramagnetic errors are largely ignored. In XSIM, we propose to keep the susceptibility maps in their native ppm range, allowing negative and positive values for both the susceptibility maps and the costs within XSIM. This change requires fine-tuning the internal parameters. We chose $$$K_1=0.01$$$, $$$K_2=0.001$$$, and $$$L=1.0$$$, to have a larger sensitivity to structural and local variance errors than to absolute deviations from zero values. This is shown in Figure 1B: errors that turn diamagnetic sources into paramagnetic sources are highly penalized.
A side benefit of keeping the original QSM dynamic range is that it avoids SSIM-hacking. In SSIM, both target and ground-truth are scaled into the [0,255] range, so extremely high or low outlying or artifactual susceptibility values can compress all the meaningful data into a very small range, leading to unusually high SSIM scores. This is represented in Figure 2, where streaking artifacts “hack” the SSIM metric. XSIM and RMSE correctly penalize these errors.
We evaluated the performance of SSIM and XSIM on FANSI⁷ QSM reconstructions of local field maps from the RC1 in-vivo single-orientation acquisition², using χ₃₃ as a ground-truth. Further validation of both metrics was performed by analyzing reconstructions of simulated local field maps⁴ submitted to RC2 and comparing the performance of XSIM and SSIM against the RMSE, Correlation Coefficient, and Mutual Information metrics. RC2:SIM2 contained a strong calcification that led to severe streaking in most submissions⁴, making this a candidate for SSIM-hacking. Source code for calculating XSIM is openly available in the FANSI Toolbox repository⁸.

RESULTS

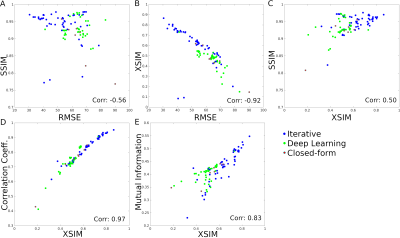
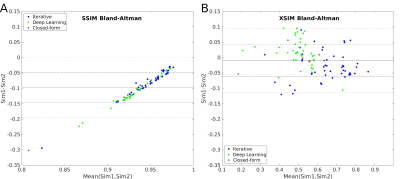
Figure 3 shows the metric scores as a function of regularization weight and optimal reconstructions for each metric. XSIM achieved the sharpest results, and the lowest regularization weights. Comparisons between global metrics for the RC2 submissions are shown in Figure 4. XSIM shows a strong correlation with RMSE and the Correlation Coefficient, fixing SSIM-hacking issues. This is also shown in Figure 5, where SSIM showed a strong bias to higher scores in RC2:SIM2 than SIM1. This bias was stronger for submissions with larger streaking artifacts (Fig 5A) and is absent with XSIM (Fig. 5B).

DISCUSSION

XSIM-optimized reconstructions look closer to the ground truth than reconstructions optimizing SSIM and RMSE. XSIM also provides greater sensitivity to changes in the regularization weight (Figure 3), making it more suitable for QSM parameter optimization. Highly localized errors are penalized less than for RMSE (Figure 2). Blurred and low-intensity reconstructions are heavily penalized (Figure 3) demonstrating that the XSIM quickly falls to zero for over-regularized solutions. Both factors lead to smaller regularization weights when optimizing using XSIM and mean that XSIM promotes a more similar global appearance to the ground truth since it does not over-penalize localized strong errors (i.e. streaking).

CONCLUSION

The SSIM metric for image comparison can correlate well with human perception of visual similarity for natural images. However, it must be properly tuned for specific imaging applications. Our XSIM implementation provides a set of parameters optimized for robust application to QSM, preventing bias and metric-hacking, and promoting sharp results.

Acknowledgements

We thank Cancer Research UK Multidisciplinary Award C53545/A24348, Fondecyt 1191710, PIA-ACT192064, and the Millennium Science Initiative Program – NCN17_129, of the National Agency for Research and Development, ANID for their funding support. Karin Shmueli is supported by European Research Council Consolidator Grant DiSCo MRI SFN 770939.