2363

Phase filtering methods significantly impact the quality of susceptibility tensor reconstruction

Jingjia Chen¹ and Chunlei Liu^1,2
¹Electrical Engineering and Computer Sciences, University of California, Berkeley, Berkeley, CA, United States, ²Helen Wills Neuroscience Institute, University of California, Berkeley, Berkeley, CA, United States

Synopsis

Phase filtering is a very important step in obtaining a good susceptibility tensor. We compare and illustrate the effects of different phase processing methods on the quality of susceptibility tensor reconstruction with different numbers of orientations. In general, tensor reconstructed from variations of the SHARP phase filtering methods show the most robustness against the large field inhomogeneity and produce tensor elements that are spatially and anatomically more consistent. Compared to the original STI reconstruction, asymmetric STI reduces some of the variations induced by phase filtering methods.

Introduction

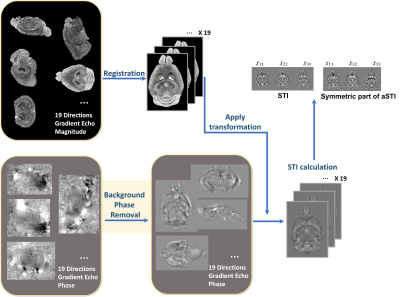
Biological tissue’s magnetic susceptibility perturbs the magnetic field inside the MRI scanner. The phase of gradient echo (GRE) signals captures this perturbation¹. Quantitative susceptibility mapping (QSM)² measures the scalar magnetic susceptibility. On the other hand, susceptibility tensor imaging (STI) measures the anisotropic susceptibility via a second-order tensor. Along with diffusion tensor imaging (DTI), STI provides complimentary information on the structure anisotropy of biological tissue³. STI reconstruction generally follows the pipeline shown in Figure1: phase of the GRE signal is unwrapped and filtered to remove the background field, followed by aligning measurements from all angles to one reference orientation. Several background phase removal algorithms exist and they have a significant impact on the accuracy of QSM maps^4,5. Since STI measures susceptibility variations across different orientations, variations due to phase processing will introduce errors in the tensor estimation. Here, we compare six commonly used methods of phase filtering in two tensor reconstruction methods to investigate the effects of background phase removal methods on the quality of STI.

Methods

GRE data of a postmortem mouse brain were collected at 19 orientations⁶. Briefly, the imaging parameters were: B0=7T, TE/TR=8.0/50ms, voxel-size=0.08mm isotropic.

The phase was unwrapped with the Laplacian-based phase unwrapping method². Afterwards, six major phase filtering methods were included in the test. Sources of MATLAB scripts are as follows: Sophisticated Harmonic Artifact Reduction for Phase⁷ (SHARP), Laplacian Boundary Value⁸ (LBV) and Regularization-enabled SHARP⁹ (RESHARP) ware obtained from online resources¹⁰, Projection onto dipole fields¹¹ (PDF) was obtained from MEDI toolbox^12,13, improved HARmonic (background) PhasE REmovaL using the Laplacian operator¹⁴ (iHARPERELLA) and Variable-radius SHARP¹⁵ (VSHARP) were obtained from STISuite¹⁶. All methods were used with masks with potential boundary erosion size considered, ensuring the output tissue phase are in the same shape and size. Parameters used for each method are iHARPERELLA: padsize=12; RESHARP: kernel_size=3, tolerance=0.001; LBV: tolerance=0.01; SHARP: kernel_size=3; tolerance=0.05; V-SHARP: smvsize=12.

Registration was performed using ITKsnap¹⁷ on each orientation’s magnitude image. After manual alignment with the reference volume, a mutual information metric was used to obtain affine transformations, which were then applied to the filtered phase. Regular symmetric STI¹⁶ reconstruction and the recently introduced asymmetric STI¹⁸ (aSTI) were used to reconstruct the tensor. Susceptibility anisotropy (SA) defined as $$$\text{SA}=\text{eigVal}(1) - (\text{eigVal}(2)+\text{eigVal}(3))/2$$$ was calculated from eigen-decomposition of the tensor (the first eigenvalue is the largest). This SA quantity was used to weigh the primary eigenvector in color-coded maps.

Results

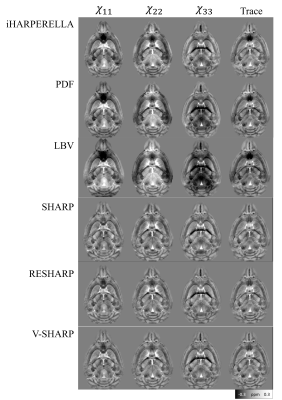
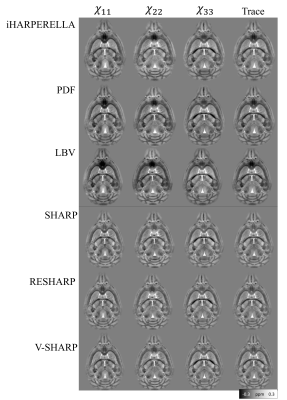
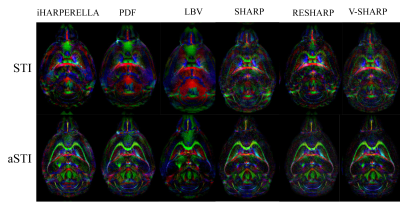
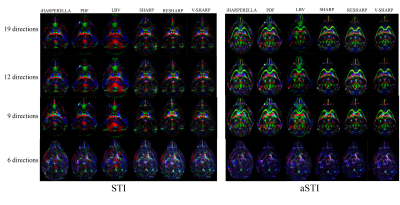
The iHARPERELLA, PDF and LBV methods result in tensor maps with significant variations that appear artificial as seen from the “dark” patches (Figure2). On the other hand, the SHARP, RESHARP and V-SHARP methods produce relatively consistent tensor maps that are free of such large “dark” patches (Figure2). Interestingly, regardless of the phase processing method, the artifacts seen in Figure2 are significantly reduced by using aSTI reconstruction (Figure3). The corresponding SA weighted primary eigenvector RGB map also shows similar results: variations of SHARP give vector maps that are more spatially coherent and aSTI is more robust to phase artifacts (Figure4). All methods, regardless of reconstruction algorithm used, have increased noise with decreasing orientation number and fail to produce meaningful results at 6 measurement orientations (Figure5).

Discussion

It was previously reported⁵ that LBV and PDF are more accurate for noiseless data in simulations, however, for in vivo cases, where there exist large frequency shifts caused by air-water boundaries (e.g. sinus), SHARP based methods outperform LBV and PDF. We have observed similar effects. The artifacts from large air bubbles on the boundary of the ex vivo sample were successfully filtered by RESHARP, SHARP, and V-SHARP (Figures 2 and 3). More importantly, the phase filtering errors associated with iHARPERELLA, PDF and LBV vary significantly between orientations, resulting in significant errors in the tensor estimation and subsequently in the eigenvectors and eigenvalues. While these errors are prominent in the original symmetric STI reconstruction, aSTI is known¹⁸ to be more robust by absorbing artifacts into the antisymmetric part of the tensor. With both STI and aSTI, it’s consistently observed that variations of the SHARP (SHARP, RESHARP, V-SHARP) methods and iHARPERELLA return more coherent eigenvectors.

As expected, tensors computed from all filtering methods become noisier with fewer directions. All methods failed when only 6 orientations of measurements were used, which suggests the minimum number of orientations needed for STI is 6 due to the lack of precise a priori control of the orientations.

Note that every method included here contains some level of flexibility of parameters tuning, while PDF requires pre-estimated noise level map for better performance. The parameters used in this study were chosen to achieve the reasonable results by visual inspections. The proper parameter choice may vary depending on the quality of raw unwrapped phase, which requires further systematic investigation.

Conclusion

V-SHARP, RESHARP and SHARP showed the most robustness towards large field perturbations close to the boundary, resulting in the most consistent tensor estimations. The aSTI method outperforms the conventional STI method in reducing phase filtering artifacts. With the same phase data, different phase filtering methods (or parameter choices) may yield informative or nearly useless STI anisotropy information. It is therefore critical to ensure that the background phase removal process was done properly and consistently across different orientations.

Acknowledgements

The authors thank Victor Han for proofreading.

References

(1) Wang, Y.; Liu, T. Quantitative Susceptibility Mapping (QSM): Decoding MRI Data for a Tissue Magnetic Biomarker. Magn. Reson. Med. 2015, 73 (1), 82–101. https://doi.org/10.1002/mrm.25358.

(2) Li, W.; Wu, B.; Liu, C. Quantitative Susceptibility Mapping of Human Brain Reflects Spatial Variation in Tissue Composition. NeuroImage 2011, 55 (4), 1645–1656. https://doi.org/10.1016/j.neuroimage.2010.11.088.

(3) Liu, C.; Murphy, N.; Li, W. Probing White-Matter Microstructure with Higher-Order Diffusion Tensors and Susceptibility Tensor MRI. Front. Integr. Neurosci. 2013, 7. https://doi.org/10.3389/fnint.2013.00011.

(4) Robinson, S. D.; Bredies, K.; Khabipova, D.; Dymerska, B.; Marques, J. P.; Schweser, F. An Illustrated Comparison of Processing Methods for MR Phase Imaging and QSM: Combining Array Coil Signals and Phase Unwrapping. Nmr Biomed. 2017, 30 (4). https://doi.org/10.1002/nbm.3601.

(5) Fortier, V.; Levesque, I. R. Phase Processing for Quantitative Susceptibility Mapping of Regions with Large Susceptibility and Lack of Signal. Magn. Reson. Med. 2018, 79 (6), 3103–3113. https://doi.org/10.1002/mrm.26989.

(6) Liu, C.; Li, W.; Wu, B.; Jiang, Y.; Johnson, G. A. 3D Fiber Tractography with Susceptibility Tensor Imaging. NeuroImage 2012, 59 (2), 1290–1298. https://doi.org/10.1016/j.neuroimage.2011.07.096.

(7) Schweser, F.; Deistung, A.; Lehr, B. W.; Reichenbach, J. R. Quantitative Imaging of Intrinsic Magnetic Tissue Properties Using MRI Signal Phase: An Approach to in Vivo Brain Iron Metabolism? NeuroImage 2011, 54 (4), 2789–2807. https://doi.org/10.1016/j.neuroimage.2010.10.070.

(8) Zhou, D.; Liu, T.; Spincemaille, P.; Wang, Y. Background Field Removal by Solving the Laplacian Boundary Value Problem. NMR Biomed. 2014, 27 (3), 312–319. https://doi.org/10.1002/nbm.3064.

(9) Sun, H.; Wilman, A. H. Background Field Removal Using Spherical Mean Value Filtering and Tikhonov Regularization. Magn. Reson. Med. 2014, 71 (3), 1151–1157. https://doi.org/10.1002/mrm.24765.

(10) Hongfu, S. QSM GitHub Repo; https://github.com/sunhongfu/QSM.

(11) Liu, T.; Khalidov, I.; de Rochefort, L.; Spincemaille, P.; Liu, J.; Tsiouris, A. J.; Wang, Y. A Novel Background Field Removal Method for MRI Using Projection onto Dipole Fields (PDF). NMR Biomed. 2011, 24 (9), 1129–1136. https://doi.org/10.1002/nbm.1670.

(12) MEDI Toolbox; http://pre.weill.cornell.edu/mri/pages/qsm.html.

(13) Liu, T.; Liu, J.; Rochefort, L. de; Spincemaille, P.; Khalidov, I.; Ledoux, J. R.; Wang, Y. Morphology Enabled Dipole Inversion (MEDI) from a Single-Angle Acquisition: Comparison with COSMOS in Human Brain Imaging. Magn. Reson. Med. 2011, 66 (3), 777–783. https://doi.org/10.1002/mrm.22816.

(14) Li, W.; Wu, B.; Liu, C. An Improved Method for Integrated 3D Phase Unwrapping and Background Phase Removal. Proc Intl Soc Mag Reson Med 2015, 3313.

(15) Wu, B.; Li, W.; Guidon, A.; Liu, C. Whole Brain Susceptibility Mapping Using Compressed Sensing. Magn. Reson. Med. 2012, 67 (1), 137–147. https://doi.org/10.1002/mrm.23000.

(16) STISuite; https://people.eecs.berkeley.edu/~chunlei.liu/software.html.

(17) Yushkevich, P. A.; Piven, J.; Hazlett, H. C.; Smith, R. G.; Ho, S.; Gee, J. C.; Gerig, G. User-Guided 3D Active Contour Segmentation of Anatomical Structures: Significantly Improved Efficiency and Reliability. NeuroImage 2006, 31(3), 1116–1128. https://doi.org/10.1016/j.neuroimage.2006.01.015.

(18) Cao, S.; Wei, H.; Chen, J.; Liu, C. Asymmetric Susceptibility Tensor Imaging. Magn. Reson. Med. 2021, 86 (4), 2266–2275. https://doi.org/10.1002/mrm.28823.

Figures

Figure 1. General pipeline of susceptibility tensor reconstruction. The background phase removal step is a key step. Many algorithms are developed to achieve accurate local tissue phase estimation. The key part of this study is to investigate how different phase filtering methods affect the final tensor results.

Figure 2. Original STI: Tensor reconstructed with the symmetry constraint using 6 different phase filtering methods. SHARP, RESHARP, and V-SHARP show the least artifacts in the diagonal tensor elements. In terms of the most artifacts, LBV particularly shows the most prominent artificial features.

Figure 3. Asymmetric STI: Tensor reconstructed without the symmetry constraint using 6 different phase filtering methods. The diagonal elements shown here are from the symmetric part of the asymmetric susceptibility tensor. Tensor elements show reduced artifacts compared to Figure 2. Overall, SHARP, RESHARP, and V-SHARP show the least artifacts in the tensor elements.

Figure 4. The susceptibility anisotropy (SA) weighted primary eigenvector RGB map. SHARP, V-SHARP and RESHARP show the most spatially coherent eigenvectors. aSTI reconstruction appears to be more robust in revealing susceptibility anisotropy even with phase artifacts. Green:L-R, Red: A-P; Blue: S-I.

Figure 5. The susceptibility anisotropy (SA) weighted primary eigenvector RGB map for 19, 12, 9 and 6 different directions of measurements. All methods crash when only 6 orientations are available. RESHARP and V-SHARP return the most reliable susceptibility tensor. At 9 orientations, the external capsule still stands out in REAHRP and V-SHARP filtered phase with conventional STI reconstruction. Green:L-R, Red: A-P; Blue: S-I.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

2363

DOI: https://doi.org/10.58530/2022/2363