Introduction

Quantitative Susceptibility Mapping (QSM) is an MRI contrast mapping the magnetic susceptibility of tissue in vivo from gradient echo measurements. The inverse problem in QSM is ill-posed requiring the use of regularization. Bayesian inference approaches such as Morphology Enabled Dipole Inversion (MEDI) use an edge-weighted gradient under an L1 norm to penalize the streaking artifacts arising from dipole-incompatible sources (such as noise) in the phase of the gradient echo data [1], [2]. However, contiguous areas of dipole-incompatibility may exist in the phase such as low signal regions in bone or air and residual background field whose source is outside the region of interest. These induce shadow artifacts that are insufficiently suppressed by this regularization. Exploiting the spherical mean value (SMV) property of the harmonic background field [3] and including it in the dipole kernel (MEDI-SMV) suppresses many of these artifacts at the cost of an eroded brain mask. A downsampled edge-weighted gradient under an L1 norm suppresses shadow artifacts at the cost of reduced regions of interest (ROI) susceptibilities [4]. Imposing an L2 norm term to minimize variation within cerebral spinal fluid reduces some shadow artifacts, termed MEDI+0 [5].

The phase error map obtained during the nonlinear multi-echo field fitting in this study locates sources of dipole-incompatibilities that may generate shadow artifacts. The reduction of shadow artifacts via an L2 norm minimizing variation within contiguous regions in the phase error map is demonstrated in this work.

Methods

The cost function in MEDI+0 is:
$$\chi(\textbf{r})= \mathrm{argmin}_\chi {\lVert w(e^{ib}-e^{id*\chi}) \rVert}_2^2+\lambda_1{\lVert M \nabla\chi \rVert}_1+\lambda_2{\lVert M_{CSF}(\chi-\bar{\chi}_{CSF}) \rVert}_2^2 \tag{1}$$
where $$$b$$$ is the relative difference field, $$$d$$$ the dipole kernel, $$$\chi$$$ the susceptibility, $$$w$$$ the noise weighting matrix, $$$M$$$ the morphological weighting matrix, $$$\nabla$$$ the gradient operator, $$$M_{CSF}$$$ the CSF mask and $$$\bar{\chi}_{CSF}$$$ the mean susceptibility within such mask.

By considering that shadow originating from larger dipole-incompatible sources can be viewed as streaking artifacts of those same sources in a lower resolution image, MEDI-d proposed:
$$\chi(\textbf{r})= \mathrm{argmin}_\chi {\lVert w(e^{ib}-e^{id*\chi}) \rVert}_2^2+\lambda_1{\lVert M \nabla\chi \rVert}_1+\lambda_2{\lVert M_{D} D \nabla \chi \rVert}_1 \tag{2}$$
where $$$D$$$ is a downsampling operator and $$$M_D$$$ is the edge mask derived from the downsampled image $$$Dm$$$ with the sum of squares across echoes of the gradient echo signal using the same method in which $$$M$$$ was derived from. The downsampling term is retained in MEDI-FM, which is defined as:
$$\chi(\textbf{r})= \mathrm{argmin}_\chi {\lVert w(e^{ib}-e^{id*\chi}) \rVert}_2^2+\lambda_1{\lVert M \nabla\chi \rVert}_1+\lambda_2{\lVert M_{CSF}(\chi-\bar{\chi}_{CSF}) \rVert}_2^2+\lambda_3{\lVert M_{S}M_{D} D \nabla \chi \rVert}_1+\sum^{n_{FM}}_j {\lVert M_j(\chi-\bar{\chi}_j) \rVert}_2^2 \tag{3}$$
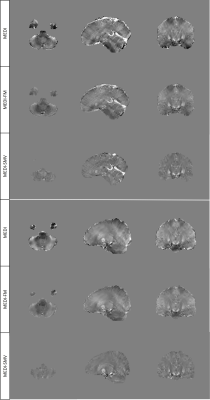
$$$\chi_{j}$$$ is the mean susceptibility within masks $$$M_{j}$$$, which are obtained as follows. The local field error map $$$E_{f}$$$ obtained during multi-echo complex field fitting is smoothed using a Gaussian kernel $$$\sigma = 3 \cdot \mathrm{min}(voxel \: size)$$$ obtaining $$$E_{f}^S$$$. Two masks $$$M_f$$$ and $$$M_{f}^S$$$ are obtained by retaining those voxels with intensity larger than half of the mean signal of a 3D patch around that voxel for $$$E_{f}$$$ and $$$E_{f}^S$$$, respectively. The connected components in $$$M_{f}^S$$$ are multiplied with $$$M_{f}$$$ to obtain the masks $$$M_{j}$$$. The additional downsampling mask $$$M_{S}$$$ is obtained by inverting $$$M_{f}$$$, followed by erosion.

Seven patients (six healthy volunteers and one hemorrhage patient) were scanned at 3T (GE Healthcare) using a 3D multi-echo spoiled gradient echo sequence. Acquisition parameters were FOV = 24 cm, partial FOV factor = 0.8, acquisition matrix size = 384 × 384 × 64, flip angle = 20°, slice thickness = 2 mm, TR = 52 msec, number of echoes = 11, first TE = 4.1 msec, echo spacing = 4.4 msec, parallel imaging factor 2, scan time of ~8 minutes. Regularization parameters were $$$\lambda_1 = 1000$$$, $$$\lambda_2 = 200 $$$, and $$$\lambda_3 = 250 $$$ and $$$\lambda_4 = 15$$$ was selected to balance ROI susceptibility and shadow reduction in healthy subject reconstructions. The downsampling parameter $$$\lambda_3$$$ was set to 0 for the first 2 iterations of the Gauss-Newton solver used for minimizing Equation 2 and halved for each iteration after iteration 3. The hemorrhage reconstruction used $$$\lambda_1 = 1000$$$, $$$\lambda_2 = 200 $$$, $$$\lambda_3 = 1000$$$, and $$$\lambda_4 = 5$$$ for all iterations, with $$$M_{S}$$$ set to the identity matrix $$$I$$$.

Results

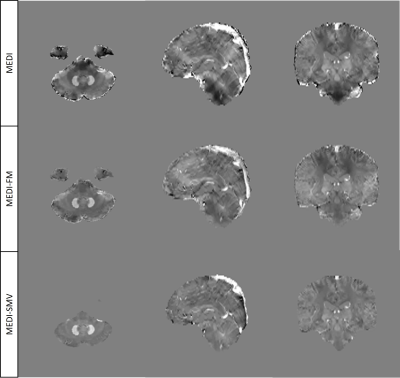
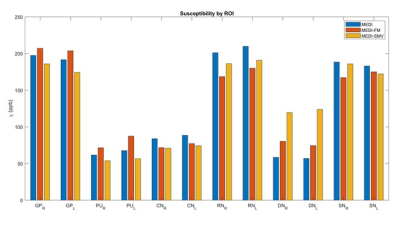
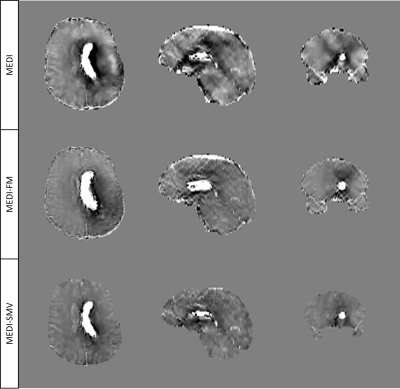
Enforcing similar susceptibility distributions within the masks displayed in Figure 1 reduces shadow artifacts in healthy subjects (Figure 2, 4) while preserving ROI susceptibilities (Figure 3). The ROIs evaluated are the left and right globus pallidus (GP), putamen (PU), caudate nucleus (CN), red nucleus (RN), dentate nucleus (DN), and the substantia nigra (SN). MEDI-FM also reduces shadow artifacts surrounding the hemorrhage in the hemorrhage case (Figure 5).

Discussion

Contiguous dipole-incompatible points with abrupt changes in susceptibility and low signal to noise ratio (SNR) are captured in the local field error map. Regularizing these regions reduces shadow artifacts. Future work involves separation of the sagittal sinus vein and the edge of the brain in $$$M_{j=1}$$$ and automatic parameter tuning to allow each component of the error map to weight the cost function by error magnitude.

Conclusion

Shadow artifacts are reduced by MEDI-FM, which regularizes susceptibility distribution in regions with high phase noise as measured by the local field error map. MEDI-FM reduces shadow artifacts in both healthy subjects and hemorrhage cases, requiring no brain erosion and preserving ROI susceptibilities.

Acknowledgements

No acknowledgement found.