Introduction

bSSFP Magnetic Resonance Fingerprinting (MRF) estimates T1 and T2 values simultaneously. bSSFP-MRF keeps the spin history with a high SNR and scan efficiency. Nevertheless, bSSFP-MRF with spiral acquisitions is prone to artifacts produced by off-resonance affecting the quality of the tissue maps. Here, we propose a UNet feed with fingerprints corrupted by off-resonance to generate corrected fingerprints with only aliasing in the bSSFP-MRF sequence. The feasibility of the proposed approach was evaluated in simulations and in-vivo brain data.

Method

Dataset: we simulated 10000 acquisitions of bSSFP-MRF¹using realistic brain parameters coming from BrainWeb's². The simulations were done with and without off-resonance effects. We employed Flip Angles (FA) between 0º-80ºafter an RF inversion pulse, 1000 random Time Repetitions (TR) between 14.5-18.0 ms, and a balanced spiral readout of 15 interleaved with 5.6 ms of readout-time. Two million fingerprints (200 per simulation) were extracted randomly to train the UNet. The data was splitted into 80% (train), 15% (validation) and 5% (test).

One volunteer was acquired with bSSFP-MRF using a FOV of 256 mm and a resolution of 2 mm, the scan duration was 14.7 s on a 1.5 T Phillips Achieva scanner (acquisition parameters equal to simulations). To evaluate the performance of our method for in-vivo, we acquired ground-truth map. We employed an inversion recovery spin echo sequence (14 TRs 100-5000 ms with TE of 7 ms, acquisition time 3 min 7 s) and a spin-echo sequence (16 echoes with TEs 15-240 ms with a TR of 3000 ms, acquisition time 3 min 35 s) to estimate T1 and T2. An exponential fitting per pixel was done for T1 and T2 maps.

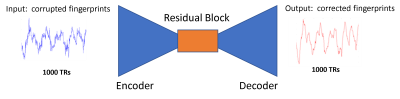
Model Architecture: we used a UNet which consists of a series of 1D convolutional, batch normalization and max pooling, and the bottleneck has several residual blocks similar to Earthquake Transfomer³. The objective function was the minus cosine similarity:
$$\mathfrak{L}(\theta ) = - \frac{\mathbf{y} \cdot \mathbf{\widehat{y}(\theta)}}{\left \| \mathbf{y} \right \| \left \| \mathbf{\widehat{y}(\theta)} \right \|}$$

where $$$\theta$$$ is the neural network parameter, $$$y$$$ is the ground-truth and $$$\widehat{y}$$$ is the neural network prediction. We solved iteratively: $$$\underset{\theta}{\text{min}} \mathfrak{L}(\theta ) $$$. Figure 1 shows a pictorial representation of the Neural Network.

Dictionary Generation: a Bloch simulator was used to generate fingerprints following a range of T1and T2 values: T1(400 to 2000 ms, every 10 ms) and T2 (40 to 300 ms, every 4 ms). The echo time (TE) was constant and equal to 5.6 ms for each TR. Tissue property maps were obtained by performing the measured signal to the closest dictionary entry using the maximum dot product.

To analyze the results, we used visual inspection and Normalized Mean Square Error: $$$NMSE(y,\widehat{y}) = \sqrt{ \frac{\left \| y-\widehat{y} \right \|_{2}^{2}}{\left \| y \right \|_{2}^{2}} }$$$, where $$$y$$$ represents the ground-truth maps (T1 or T2) and $$$\widehat{y}$$$ its estimation.

Results

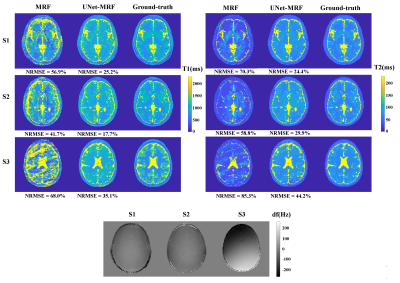
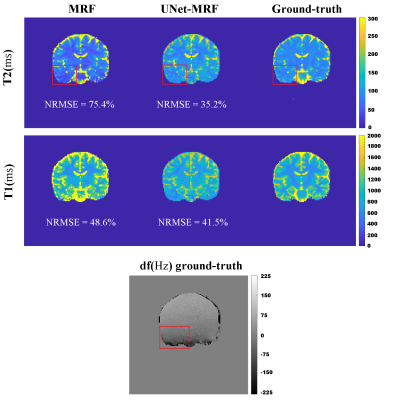
Figures 2 shows the results of a standard reconstruction and our correction method. Considerable NRMSE reduction from MRF to UNet-MRF for T1/T2 maps was achieved. For example, for simulation S1 the T1/T2 NRMSEs were reduced from 59.9%/70.3% (MRF) to 25.2%/24.4% (UNet-MRF). UNet-MRF reduced in simulations (S1, S2 and S3) theT1/T2 NRMSE values by around 50% with respect to MRF. Note that these numerical phantoms are heavily affected by off-resonance artifacts, with values in $$$\pm 3.5 $$$ ppm (-220 Hz to 220 Hz at 1.5 T).

Figure 3 shows a brain acquisition in a volunteer. The T1/T2 NRMSEs were decreased from 48.6%/75.4% (MRF) to 41.5%/35.5% (UNet-MRF). The red squared point outs in the field map a region with a high spatial off-resonance variation. And, For T2, UNet-MRF improves the map reconstruction considerably from classical MRF, recovering tissue structures.

However, artifacts associated with aliasing and off-resonance remains using UNet-MRF. This is because we are using only temporal 1D convolution in the UNet. In the future, we will work using spatial patches where we can exploit not only temporal but also spatial correlations⁴.

Conclusion

A general approach based on UNet was proposed to correct for off-resonance distortions in bSSFP-MRF with spiral sampling. Our approach for off-resonance correction showed improved reconstructions in comparison to conventional bSSFP-MRF. Future work will be to include spatial correlations to decrease aliasing and off-resonance artifacts.