2355
Distortion correction in multi-echo MRI without field mapping or reverse encoding
Yael Balbastre1,2, Divya Varadarajan1,2, Klara Bas3, John Ashburner3, Robert Frost1,2, and Bruce Fischl1,2,4
1Athinoula A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Charlestown, MA, United States, 2Department of Radiology, Harvard Medical School, Boston, MA, United States, 3Wellcome Center for Human NeuroImaging, Queen Square Institute of Neurology, University College London, London, United Kingdom, 4Computer Science and Artificial Intelligence Laboratory, Massachusetts Institute of Technology, Cambridge, MA, United States
1Athinoula A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Charlestown, MA, United States, 2Department of Radiology, Harvard Medical School, Boston, MA, United States, 3Wellcome Center for Human NeuroImaging, Queen Square Institute of Neurology, University College London, London, United Kingdom, 4Computer Science and Artificial Intelligence Laboratory, Massachusetts Institute of Technology, Cambridge, MA, United States
Synopsis
Low-bandwidth multi-echo acquisitions suffer from spatial distortions between odd and even echoes caused by B0 homogeneity, causing blurs and loss of effective resolution in sum-of-square images or derived quantitative parameters. We show in this abstract that this curse can also be beneficial, as it allows distortions to be mapped without the need for additional field mapping data. We do so by jointly optimizing a forward model of the data with respect to exponential decay parameters and a smooth distortion map.
Introduction
Spatial distortions caused by susceptibility-induced field inhomogeneities are a well-known problem in echo-planar imaging (EPI) but are also starting to be investigated in 3D gradient-echo (GRE) imaging, where the push for higher resolution and lower bandwidth makes the acquisition susceptible to even small deviations from nominal B0. This issue is particularly present in very high resolution ex vivo imaging, where the use of extremely low bandwidths can cause distortions of several (very small) pixels in the readout direction1; and in high-resolution structural imaging2, where even small artefacts can hamper the detection of longitudinal changes.Multi-echo acquisitions are used more and more frequently in this context, in order to minimize distortions and dead time3. These datasets can be used to recover quantitative MR parameters, or combined more straightforwardly in a sum-of-squares to increase SNR. Furthermore, as odd and even echoes are acquired with an opposite readout polarity, multi-echo sequences are naturally sensitive to distortions. While these distortions between echoes currently cause misalignment and blurring, they also offer a potential avenue to estimate high-resolution fieldmaps without the need for additional data; a potential that has been untapped so far.
In contrast with TopUp4, which requires blip-up and blip-down images that share the same contrast, we propose Multi-Echo TopUp: a generative model of multi-echo data that jointly fits an exponential decay and the distortion map that maximizes its goodness of fit. This allows distortions to be corrected in multi-echo images without the need for additional field mapping data. This method also differs from 5, where the exponential model was used to synthesize reversed versions of each echo that were then matched in a TopUp manner. The proposed algorithm can be related to methods that perform model fitting and motion (or other sorts of distortions) estimation jointly6–8.
Methods
We write the joint likelihood of the data and unknown parameters as$$p(\mathbf{X}, \boldsymbol\Theta, \mathbf{d}) = \prod_{e=1}^{N_e} p\left(\mathbf{x}_e \mid s(\boldsymbol\Theta, t_e), \mathbf{d}\right) \times p(\boldsymbol\Theta) \times p(\mathbf{d}) ~,$$
where $$$\mathbf{X} \in \mathbb{R}^{M \times N_e}$$$ are the $$$N_e$$$ acquired echoes (with $$$M$$$ voxels), $$$\mathbf{d} \in \mathbb{R}^M$$$ is the displacement field, that gets multiplied by the parity of each echo, $$$\boldsymbol\Theta \in \mathbb{R}^{M \times 2}$$$ contains the intercept and decay parameters and $$$s$$$ is the decaying exponential function. We choose a distribution that penalizes the bending energy for $$$p(\mathbf{d})$$$, and an edge-preserving joint total-variation (JTV) distribution for $$$p(\boldsymbol\Theta)$$$. While it is common to use a Gaussian approximation for the likelihood term $$$p(\mathbf{x}_e \mid s(\boldsymbol\Theta, t_e), \mathbf{d})$$$, we found it to be too sensitive to background noise and low-SNR regions, and use a non-central Chi distribution instead. The non-central Chi likelihood is implemented in a reweighted fashion9, such that we are left with a nonlinear least-squares problem with respect to $$$\boldsymbol\Theta$$$ and $$$\mathbf{d}$$$. Note that in the forward model, the synthesized echo $$$s(\boldsymbol\Theta, t_e)$$$ is deformed by $$$\pm\mathbf{d}$$$ and modulated by its Jacobian determinant $$$1 \pm \nabla \mathbf{d}$$$. Our implementation alternates between optimizing the joint log-likelihood with respect to $$$\boldsymbol\Theta$$$ and $$$\mathbf{d}$$$, and uses a robust version of Gauss-Newton10 where each quadratic step is solved efficiently with a full-multi grid solver11. The nonsmooth JTV prior is implemented using an iteratively reweighted scheme10.
The proposed method was tested on two ex vivo cases (whole hemisphere and cerebellum) at 7T, and two in vivo cases at 3T and 7T. Sequence parameters are provided in Table 1. All cases had fieldmaps acquired with a dual-echo GRE; and the cerebellum and in vivo cases further had reversed-polarity images acquired in an interleaved fashion2 (that is, the 4 echoes are available in PNPN and NPNP orders). Our method only used one of the polarities (e.g. PNPN), whereas both versions of the first echo (i.e. P+N) were used to compute TopUp fieldmaps for comparison. We used the same TopUp parameters as in 2, which were found to be optimal for fine-grained distortion correction.
Results
Figure 1 and 2 shows the result of applying all three methods to multi-echo MPRAGE data at 3T and 7T. All methods can successfully recover distortions caused by the air-tissue interface at the sphenoid sinus.Figure 3 shows that all methods can successfully correct large distortions (up to 5 voxels) in an image of the ex vivo cerebellum.
Conclusion
We demonstrated that accurate fieldmaps can be estimated from multi-echo images without requiring a second scan with reverse polarities, and that they can be used to correct substantial distortions in low bandwidth images, both in vivo and ex vivo. This method only requires magnitude data and can be applied retrospectively to any existing multi-echo dataset.Acknowledgements
We are grateful for the following funding sources: U01MH117023, R01AG064027, P41EB030006.References
- Varadarajan, D. et al. Edge-preserving B0 inhomogeneity distortion correction for high-resolution multi-echo ex vivo MRI at 7T. in Proc. Intl. Soc. Mag. Reson. Med. (2020).
- Frost, R. et al. Interleaved reversed polarity MPRAGE for in vivo B0 readout distortion correction. in Proc. Intl. Soc. Mag. Reson. Med. (2020).
- van der Kouwe, A. J. W., Benner, T., Salat, D. H. & Fischl, B. Brain morphometry with multiecho MPRAGE. Neuroimage 40, 559–569 (2008).
- Andersson, J. L. R., Skare, S. & Ashburner, J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. Neuroimage 20, 870–888 (2003).
- Weiskopf, N., Klose, U., Birbaumer, N. & Mathiak, K. Single-shot compensation of image distortions and BOLD contrast optimization using multi-echo EPI for real-time fMRI. Neuroimage 24, 1068–1079 (2005).
- Jiao, J., Salinas, C. A., Searle, G. E., Gunn, R. N. & Schnabel, J. A. Joint estimation of subject motion and tracer kinetic parameters of dynamic PET data in an EM framework. in Medical Imaging 2012: Image Processing vol. 8314 96–104 (SPIE, 2012).
- Fischl, B. et al. Sequence-independent segmentation of magnetic resonance images. Neuroimage 23 Suppl 1, S69–84 (2004).
- Andersson, J. L. R. & Sotiropoulos, S. N. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. Neuroimage 125, 1063–1078 (2016).
- Varadarajan, D. & Haldar, J. P. A Majorize-Minimize Framework for Rician and Non-Central Chi MR Images. IEEE Trans. Med. Imaging 34, 2191–2202 (2015).
- Balbastre, Y. et al. Model-Based Multi-Parameter Mapping. Med. Image Anal. 102149 (2021).
- Ashburner, J. A fast diffeomorphic image registration algorithm. Neuroimage 38, 95–113 (2007).
Figures
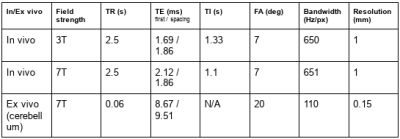
Parameters of the validation data
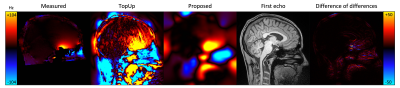
Figure 1: In vivo multi-echo MEPRAGE at 3T. From left to right, the top panel shows the distorted first echo, and the estimated field maps (in Hz) using the dual-echo, TopUp (from reversed polarities) and proposed (from a single polarity) methods.
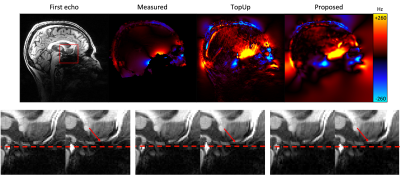
Figure 2: In vivo multi-echo MEPRAGE at 7T. From left to right, the top panel shows the distorted first echo, and the estimated field maps (in Hz) using the dual-echo, TopUp (from reversed polarities) and proposed (from a single polarity) methods. The bottom panel shows a close-up of the first echo acquired with a negative or positive polarity, before (left) and after (right) distortion correction.
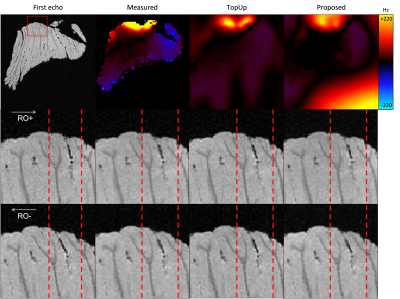
Figure 3: Cerebellum ex vivo. The top panel shows the fieldmap estimated using the dual echo, TopUp and proposed methods. The large positive offset in the bottom-right corner of the proposed fieldmap only concerns background voxel and does not have an effect on correction. The bottom panels show the positive and negative polarity images before correction (first column) and corrected with each method (second column: fieldmap; third column: TopUp; fourth column: proposed). Vertical guides are present to help the reader.
DOI: https://doi.org/10.58530/2022/2355