Introduction

In spinal cord (SC) MRI, proximity to the lungs imposes time-varying changes to the magnetic field for each imaging slice that cannot be compensated using only static gradients[1,2].
A recently introduced approach, called realtime dynamic z-shimming[3] employs dynamic (slice-wise) z-shimming with realtime adjustments of z-shimming gradients to correct for respiration-induced field changes.
However, dynamic z-shimming and realtime dynamic z-shimming methods presuppose that in-plane field gradients lead to negligible phase accrual. Here, we propose a dynamic shimming solution that compensates for both through-plane and and in-plane field gradients (”dynamic xyz-shimming”), and extend this technique to compensate for respiration-induced field gradients (“realtime dynamic xyz-shimming”).

Theory

During respiration, magnetic field gradients within the imaging(x-y) plane, $$$G_z(x,y,t), G_y(x,y,t), G_x(x,y,t)$$$ can be separated into static and realtime components:
$$$G_z(x,y,t)=G_{z,static}(x,y)+RIGO_z(x,y)\cdot P(t)$$$ [Eq.1]
$$$G_y(x,y,t)=G_{y,static}(x,y)+RIGO_y(x,y)\cdot P(t)$$$ [Eq.2]
$$$G_x(x,y,t)=G_{x,static}(x,y)+RIGO_x(x,y)\cdot P(t)$$$ [Eq.3]
Where $$$RIGO_z(x,y),RIGO_y(x,y),RIGO_x(x,y)$$$ are the amplitudes of the respiration-induced gradient offset and $$$P(t)$$$ represents a time-varying sinusoidal signal.
If $$$G_z(x,y,t),G_y(x,y,t),G_x(x,y,t)$$$ do not vary considerably in-plane[4], they can be minimised by including correction gradients within an imaging sequence along the slice-select (“z”)[4] and in-plane (“x”,“y”) directions ($$$G_{z,corr},G_{y,corr},G_{x,corr}$$$) (Fig1).

Acquisition and analysis

Scans were acquired on one volunteer (26,M) using a 3T Siemens Prisma-fit scanner and a 64 channel head-neck receiver coil. Respiratory bellows were used to monitor and log breathing, $$$P(t)$$$, throughout the session. A 3D T1-weighted scan (T1w,TR/TE=15/3.15ms, FOV=256x256x66mm, resolution=0.9x0.9x3mm,FA=15°) was acquired.
Then a series of 30 sequential dual-echo ΔB0 maps were acquired in the sagittal orientation covering the cervical SC (TR/TE1/TE2=35/2.14/4.6ms,2.2x2.2mm² in-plane resolution, 5 slices of 2.2mm, FA=20°). The scanner’s first and second order shim adjustment volume was optimised in the SC. The adjustment volume and first/second-order shim currents for this scan were used throughout the session.
An axial 2D multi-echo gradient-echo (MGRE) scan (noshim) was acquired (6 echoes, TR/TE1/echo spacing=189/2.5/2.2 ms, BW=600 Hz/px, 12 slices of 3 mm, matrix=128x56, image resolution=2.2x2.2 mm², FA=20°) oriented perpendicularly to the SC at C6/C7. All of the data were transferred offline via ethernet for shim calculation.

Using the log from the bellows, each ΔB0 map was associated with a pressure reading. The shimming toolbox (ST, https://shimming-toolbox.org/)[5] was used to compute the gradient along each axis for each ΔB0 map. A voxelwise linear regression between pressure and gradient was performed to derive images of static and RIGO components. The Spinal Cord Toolbox (SCT)[6] was used to generate an SC mask using the noshim scan and the static and RIGO component images were resampled and registered to the noshim scan. The mean of the static and RIGO components were calculated within the SC mask ($$$<G_{z,static}>,<G_{y,static}>,<G_{x,static}>$$$ and $$$<RIGO_z>,<RIGO_y>,<RIGO_x>$$$ ) for each slice and transferred to the scanner.

Next, 2D MGRE images were acquired using the same acquisition parameters and orientation as the noshim scan, under 4 dynamic shimming scenarios: static z-shim (ST-zshim), where the compensation gradients were only played out along the z direction and not adjusted in real time; static xyz-shimming (ST-xyzshim), where correction gradients were played out in-plane as well as through-plane; realtime z-shim (RT-zshim), where the correction gradients along the z-direction were adjusted in real time; and realtime xyz-shimming (RT-xyzshim), where correction gradients were played out along all three axes and adjusted in real time.

The $$$<G_{z,static}>,<G_{y,static}>,<G_{x,static}>$$$ and $$$<RIGO_z>,<RIGO_y>,<RIGO_x>$$$ values for each slice were read by the sequence at the start of the acquisition and the pressure on the bellows was continuously sampled by the scanner at a rate of 50Hz. For static shimming, only $$$<G_{z,static}>,<G_{y,static}>,<G_{x,static}>$$$ were taken into account. For realtime shimming, $$$<RIGO_z>,<RIGO_y>,<RIGO_x>$$$ components were used as well, modulated by bellows' pressure:
$$$<G_z>=<G_{z,static}>+<RIGO_z>\cdot P(t')$$$ [Eq.4]
$$$<G_x>=<G_{x,static}>+<RIGO_x>\cdot P(t')$$$ [Eq.5]
$$$<G_y>=<G_{y,static}>+<RIGO_y>\cdot P(t')$$$ [Eq.6]
Where $$$P(t')$$$ is the pressure measured by the respiratory bellows at a time t’, equal to the excitation time of the slice in question. Using $$$<G_z>,<G_y>,<G_x>$$$ the appropriate correction gradients are computed and played out by the sequence.

The SC was segmented from the T1w scan using SCT. This segmentation was coregistered and applied to the MGRE scans. The mean signal intensity within each slice was computed for each shim condition and echo time. The standard deviation across all slices was computed for each shim condition and echo time as the outcome metric.

Results

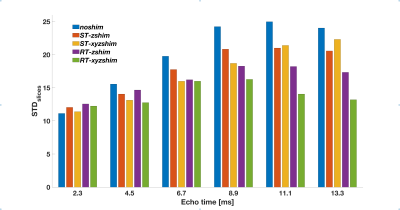
Figure 2 shows the standard deviation of signal intensity across slices (STD_slices) for each echo and each shim condition. STD_slices increased from TE1 to TE6 in the noshim condition by~115%. In the ST-zshim condition, there was an increase of~70%, for ST-xyzshim, there was an increase of~96%, for RT-zshim there was an increase of~38%, and for RT-xyzshim the increase was only~8%.

Discussion and conclusion

Our results show that in the absence of dynamic shimming, MGRE signals at later echo times are adversely affected by B₀ inhomogeneities. The use of dynamic z-shimming, which has been applied to SC imaging in the past, can improve signal homogeneity in the SC[7].
Here we show that extending this approach to account for respiration-induced magnetic field gradients can improve signal homogeneity by ~20%. If in-plane gradients are included in the realtime compensation, homogeneity can be improved by as much as ~70%.
This method is a promising approach for improving image quality in SC MRI that is sensitive to field inhomogeneities, such as T2* mapping, fMRI, or high-field MRI.

Acknowledgements

Funded by the Canada Research Chair in Quantitative Magnetic Resonance Imaging [950-230815], the Canadian Institute of Health Research [CIHR FDN-143263], the Canada Foundation for Innovation [32454, 34824], the Fonds de Recherche du Québec - Santé [28826], the Natural Sciences and Engineering Research Council of Canada [RGPIN-2019-07244], the Canada First Research Excellence Fund (IVADO and TransMedTech), the Courtois NeuroMod project and the Quebec BioImaging Network [5886, 35450].