2350
Automatic reconstruction of arbitrary MRI sequences based on phase distribution graphs
Jonathan Endres1, Hoai Nam Dang2, Felix Glang3, Alexander Loktyushin3, Simon Weinmüller2, and Moritz Zaiss2,3
1Universitätsklinik Erlangen, Erlangen, Germany, 2Department of Neuroradiology, Universitätsklinik Erlangen, Erlangen, Germany, 3Magnetic Resonance Center, Max-Planck-Institute for Biological Cybernetics, Tübingen, Germany
1Universitätsklinik Erlangen, Erlangen, Germany, 2Department of Neuroradiology, Universitätsklinik Erlangen, Erlangen, Germany, 3Magnetic Resonance Center, Max-Planck-Institute for Biological Cybernetics, Tübingen, Germany
Synopsis
We propose a method to automatically generate estimators for the exact encoding of a MRI signal, based on the Phase Distribution Graph of a sequence and its simulation. The estimator can then be used on a measurement to split the signal into its differently encoded parts, which enables reconstruction tailored to the sequence used. This approach can result in fewer imaging artifacts since it does not rely on any assumptions about the sequence made up front but on data obtained by a PDG simulation. This also makes it suitable for sequence optimization because it can adapt to changing sequence properties.
Motivation
Common approaches for reconstructing images from measured MRI signals usually assume that the signals’ samples are a direct measurement of a correctly encoded k-space, thus only requiring an inverse Fourier transformation for reconstruction. However, residual echo paths can lead to more than only the aimed-at echo which contributes to the signal but is wrongly encoded and has a different contrast. In this case the sum of different k-space locations will be measured, producing imaging artifacts. Typically, such problems are solved by introducing sufficient spoiling to suppress unwanted paths.In this work, we propose a method to gain insight into the exact encoding of the measured signal by using a simulation based on Phase Distribution Graphs [1] (PDG). This knowledge can then be transferred to a reconstruction of the signal of a real measurement, tailored to the sequence that produced it. This process, titled Automatic Reconstruction, is outlined in figure 1. Since it adapts to any measurement that can be reproduced by the simulation, it lifts restrictions set by a fixed conventional reconstruction algorithm, which is desirable for sequence optimizations. This paves the way to less coherent and more complex sequence strategies, especially involving only partially spoiled magnetization that can still be separated by Automatic Reconstruction.
Materials and Methods
Signal simulations were performed by using PDGs, which is part of the MRzero [2] framework and suitable for simulating arbitrary MRI sequences in 3D. PDGs split magnetization into distributions with known encoding, $$$T_2'$$$ dephasing, phase, and simulated magnetization, to calculate the signal.The known partition of the measured signal into individual distributions can be used to reconstruct them individually. In this work we use inverse Fourier transformation for this task and sum up the result to obtain the final image. This Automatic Reconstruction therefore does not rely on a single k-space trajectory but uses the known encoding of individual distributions, while reversing the rotation introduced by RF phase cycling. This is equivalent to automatically adjusting the ADC phase to the polarity of the echo.
We also introduce an estimator needed for estimating the signal contribution of individual distributions based on the measured signal. While all other properties of the distributions only depend on the sequence and are therefore known, their individual signals can only be estimated since it depends on the exact physical properties of the measured subject. By relying on the correlation between measured signal and individual signals of the distributions, it is possible to construct an estimator for those signals by analyzing the simulation data. The whole Automatic Reconstruction pipeline is shown in figure 2.
The estimator used in this work assumes that all distributions produce similar signals but with different amplitudes, which is adequate for sequences like bSSFP [3]. It stores the average signal of every distribution divided by the simulated signal to then multiply the measured signal with these complex factors to return signal estimates for individual distributions.
Results
The estimator used in this work produces distribution signals close to the ones obtained by simulating the sequence (fig. 3). While the estimation is not exact, this still results in noticeable improvements compared to conventional reconstruction, which can be seen as a trivial estimator that describes the magnetization consisting of one single distribution.The improvement of the resulting image can be seen in figure 4. It shows strong ghosting artifacts when using “Default” (inverse Fourier transformation) reconstruction. They are a result of using only the previous pulse to determine the ADC phase, which is insufficient in this sequence. Automatic Reconstruction splits the magnetization into different parts with known phases, reducing the imaging artifacts. The estimator was generated using a different subject to the one it was applied to, demonstrating that it can be transferred to other measurements of the sequence.
As stated above, Automatic Reconstruction is suited well for optimization. As shown in figure 5, it produces a smooth loss landscape by adapting to the sequence. Because conventional reconstruction assumes that the previous pulse is sufficient to determine the phase of the signal, the loss increases faster with increasing randomization, but also depends on how close the assumed phase matches the actual polarization of the signal. This means Automatic Reconstruction not only results in a lower loss, but also in a smoother loss landscape, and is therefore leading to faster optimization convergence.
Discussion
By utilizing the proposed pipeline, it is possible to take advantage of the PDG simulation by returning additional information about the measured signal, which can then be used to automatically reconstruct an image without the need for additional inputs. Further improvements can be made by modifying the estimator and the reconstruction used in this abstract. Nevertheless, they are a good fit for sequences producing signals with unknown polarity, where it is difficult to calculate the ADC rotation needed for reconstruction otherwise.Additionally, Automatic Reconstruction can remove restrictions when used for an end-to-end sequence optimization like in MRzero. Conventional reconstruction imposes a predefined reconstruction strategy onto the optimization, restricting its degrees of freedoms. In contrast, Automatic Reconstruction is only based on the encoding of the signal itself and can thus adapt to any change.
Acknowledgements
No acknowledgement found.References
- Endres J. et al, Phase distribution graphs for differentiable and efficient simulations of arbitrary MRI sequences, In: Joint Annual Meeting ISMRM-ESMRMB 2022
- Loktyushin, Herz, Dang, MRzero - Automated discovery of MRI sequences using supervised learning. Magn Reson Med. 2021; 86: 709– 724
- Scheffler, Lehnhardt, Principles and applications of balanced SSFP techniques. Eur Radiol. 2003 Nov; 13(11):2409-18
- http://www.bic.mni.mcgill.ca/brainweb/
Figures

Functionality
of Automatic Reconstruction. The measured signal is split into different parts
by estimating its constitution. Since the exact encoding of all parts is known
by simulating the sequence, they can be reconstructed individually. These
individual reconstructions might only be encoded partially but can be combined
into a full image. This suppresses imaging artifacts compared to conventional
reconstruction which assumes a single encoding for the signal.
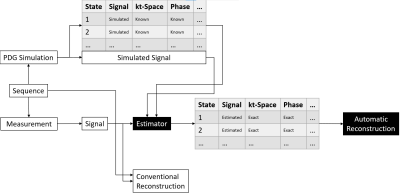
Pipeline
used for Automatic Reconstruction. The simulation provides additional
information about the simulated signal that can’t be measured. This information
is used to build an estimator that can be used on measurements to provide
estimates of the signal of all contributing distributions together with exact
information about their encoding.
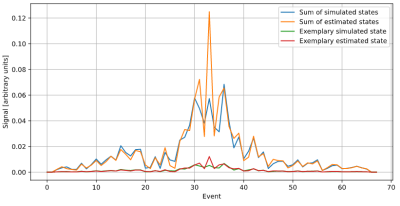
Signal of
an exemplary distribution and the sum of all distributions, compared with the
signals estimated based on the measured signal. Shown is the magnitude signal
of the central
gradient echo of a bSSFP sequence.
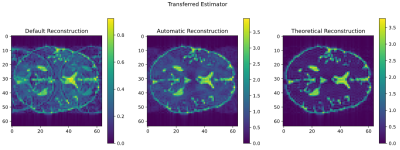
Comparison
of conventional and Automatic Reconstruction of a bSSFP sequence with 22.5°
phase error. Conventional (default) reconstruction shows severe ghosting
artifacts which are suppressed by the Automatic Reconstruction. With a perfect
estimator, one could obtain the right image, which uses the simulation data
directly. The estimator was build using the simulation of another subject than
the one shown, which demonstrates the transferability. The simulation was done
using data from the BrainWeb [4] database.
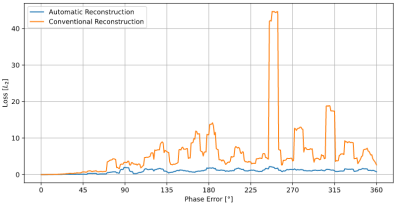
Loss
landscape bSSFP with increasing randomization of pulse phases. The
randomization is uniform in the range given by the x position in the graph. One
sample per degree was calculated, graph is smoothed using a running average
over 10 samples. The loss plotted on the y axis is the L2 norm of
the difference of
the reconstruction at any sample and the sequence without any randomization,
i.e., the sample at x = 0.
DOI: https://doi.org/10.58530/2022/2350