2349
Fast $$$T_{2}^{*}$$$ and QSM mapping using temporal CS with a Complementary Stochastic Sampling Scheme
Charles Iglehart1, Ali Bilgin1, and Manojkumar Saranathan2
1Electrical and Computer Engineering, University of Arizona, Tucson, AZ, United States, 2Department of Medical Imaging, University of Arizona, Tucson, AZ, United States
1Electrical and Computer Engineering, University of Arizona, Tucson, AZ, United States, 2Department of Medical Imaging, University of Arizona, Tucson, AZ, United States
Synopsis
We develop the motivation for and demonstrate the functionality of a temporal model-based complex multi-echo reconstruction algorithm coupled with a Complementary Stochastic Sampling procedure allowing for temporal sparsity to be leveraged . We demonstrate results for magnitude and phase images as well as parameter maps.
Introduction
$$$T_{2}^{*}*$$$ and quantitative susceptibility mapping (QSM) are increasingly used clinically for investigation of iron deposition in Parkinson's disease (1,2), hemorrhage detection (3,4), and as potential age-related biomarkers of neurodegeneration (5-7). Parametric mapping requires 3D multi-echo gradient-recalled echo (ME GRE) MRI acquisitions, which prolong long scan times at high spatial resolution (1 mm or higher). Thus, scan time reduction using k-space undersampling with high fidelity magnitude and phase reconstruction is critical. Some temporal subspace-based compressed sensing (CS) algorithms have been developed (8,9) using simulated signal evolutions to recover $$$T_{2}$$$ maps from undersampled k-space data. These are not easily translatable to complex-valued reconstruction due to scaling issues. Ong et al (10) provide a general framework for simultaneous magnitude and phase reconstruction from partial Fourier acquisitions, but only for single-echo reconstruction. Huang et al (11) developed a model-based method for simultaneous, complex-valued reconstruction from undersampled k-space data but do not show results for phase-echo images or QSM . Additionally, these CS schemes apply the same (ky,kz) sampling pattern at each echo, eliminating potential gains from temporal sparsity. In this work, we propose a Complementary Stochastic Sampling (‘COSTS’, 12) strategy with a novel interleaved, complex-valued reconstruction using separate subspace-based temporal signal models for magnitude and phase. We demonstrate results for complex multi-echo reconstructions as well as derived parameter maps from in vivo data.Methods
Figure 1 shows the proposed complex, multi-echo reconstruction using an iterative optimization that interleaves Alternating Direction Method of Multipliers (‘ADMM’, 13)-based magnitude and phase updates. Both magnitude and phase objectives are formulated using temporal model coefficients to promote sparsity. To model the temporal behavior of the magnitude images, a subspace basis $$$\Phi$$$ is computed via singular value decomposition of an ensemble of 50,000 simulated monoexponential signal evolutions with $$$T_{2}^{*}$$$ randomly selected from [0.001s,1.0s] (Figure 1A). A two-parameter linear fit is used to model the temporal behavior of unwrapped phase for voxel across the echo dimension, (Figure 1B). K-space undersampling is performed via COSTS (Figure 1C). Sampling is restricted to an annular region in order to maintain spatial resolution while avoiding corners in (ky,kz). Within the annular region, each (ky,kz) point is sampled at exactly one echo, ensuring temporal as well as spatial incoherence. The central region of k-space is fully sampled. The magnitude objective function is constructed as shown in Figure 1(D): $$$\alpha$$$ is the stack of PCC maps; $$$\Phi_{K}^{H}$$$ is the truncated temporal subspace basis; $$$S$$$ is an ESPIRIT (14) sensitivity encoding operator; $$$F$$$ is the forward Fourier operator; $$$P$$$ COSTS sampling operator; y is the acquired, undersampled k-space data; $$$\lambda_{m}$$$ is a regularization parameter; $$$R_{r}(\alpha)$$$ is an operator enforcing local low-rank structure in the magnitude PCC maps. The magnitude objective is iteratively optimized in ADMM, with the resulting PCC maps projected into the time domain to obtain reconstructed multi-echo magnitude images. These magnitudes are subsequently multiplied by the initial multi-echo phase estimate obtained from the zero-filled, undersampled k-space data to seed the phase objective function. Figure 1(D) shows the phase objective: $$$\Psi$$$ projects the estimated model coefficients into the time domain; $$$F^{H}$$$ and $$$S^{H}$$$ are the adjoints of the Fourier and ESPIRIT operators; $$$\Theta$$$ is an operator that outputs the unwrapped phase of complex multi-echo images; $$$\lambda_{p}$$$ is a regularization parameter, with phase regularization performed via the $$$L_{1}$$$ norm of total variation. As with magnitude, the phase objective is iteratively optimized in ADMM. The resulting phase model coefficients are projected into the time domain, with multi-echo images used to seed subsequent iterations of magnitude reconstruction. Magnitude and phase updates are interleaved until convergence or stopping criteria have been encountered. Multi-echo magnitude, phase, $$$M_{0}$$$, and $$$R_{2}^{*}$$$ (the latter two having been computed from the reconstructed magnitude images via ordinary least squares) are evaluated against ground truth from fully sampled data. All reconstructions and analyses are performed in Matlab using a modified version of BART Toolbox (15) as a framework. Fully-sampled ME-GRE datasets from the Cornell QSM toolbox (16) were used for retrospective undersampling. Dataset 1: Siemens 3T scanner, TR/TE 5.5/5.9ms, ETL 8; Dataset 2: GE 3T scanner, TR/TE 4.9/5.2ms, ETL 9; both datasets with voxel size 0.94 x 0.94 x 2.0 mm and 15° flip angle.Results
Figure 2-3 show reconstructed magnitude and phase for a single subject using acceleration ratios of 4 and 8, respectively. Figure 4 shows $$$M_{0}$$$ and $$$R_{2}^{*}$$$ maps for both accelerations. Figure 5 shows QSM for an ROI over a mid-axial slice.Discussion
For R = 4 (Fig 2), both magnitude and phase reconstruction reproduce finely detailed structures in the brain. Phase errors are small, primarily concentrated in CSF. For R=8 (Fig 3), the magnitude reconstruction is still accurate, with corresponding accuracy in the parameter maps; the phase images are blurrier than in the R = 4 case. The reconstructed parameter maps show larger errors in $$$R_{2}^{*}$$$, concentrated largely in CSF, while $$$M_{0}$$$ is still high quality. The accelerated QSM (Fig 5) shows good correspondence with truth with some blurring at R=8.Conclusion
We have demonstrated a multi-echo, complex reconstruction technique using temporal models coupled with COSTS. The method shows promising accuracy in multi-echo magnitude and phase images and $$$R_{2}^{*}$$$ maps, even at higher R values.Acknowledgements
(None.)References
- Naying He, Pei Huang, Huawei Ling, Jason Langley, Chunlei Liu, Bei Ding, Juan Huang, Hongmin Xu, Yong Zhang, Zhongping Zhang, et al., “Den- tate nucleus iron deposition is a potential biomarker for tremor-dominant parkinson’s disease,” NMR in Biomedicine, vol. 30, no. 4, pp. e3554, 2017.
- Qiqi Chen, Yiting Chen, Yue Zhang, Furu Wang, Hongchang Yu, Caiyuan Zhang, Zhen Jiang, and Weifeng Luo, “Iron deposition in parkinson’s disease by quantitative susceptibility mapping,” BMC neuroscience, vol. 20, no. 1, pp. 1–8, 2019.
- Franz Fazekas, Reinhold Kleinert, Gudrun Roob, Gertrude Kleinert, Pe- ter Kapeller, Reinhold Schmidt, and Hans-Peter Hartung, “Histopatho- logic analysis of foci of signal loss on gradient- echo t2*-weighted mr im- ages in patients with spontaneous intracerebral hemorrhage: evidence of microangiopathy-related microbleeds,” American Journal of Neuroradiol- ogy, vol. 20, no. 4, pp. 637–642, 1999.
- Mohammad I Zia, Nilesh R Ghugre, Kim A Connelly, Bradley H Strauss, John D Sparkes, Alexander J Dick, and Graham A Wright, “Characterizing myocardial edema and hemorrhage using quantitative t2 and t2* mapping 3 at multiple time intervals post st-segment elevation myocardial infarction,” Circulation: Cardiovascular Imaging, vol. 5, no. 5, pp. 566–572, 2012.
- Alisdair McNeill, D Birchall, SJ Hayick, Allison Gregory, JF Schenk, EA Zimmerman, H Shang, H Miyajima, and PF Chinnery, “T2* and fse mri distinguishes four subtypes of neurodegeneration with brain iron accumulation,” Neurology, vol. 70, no. 18, pp. 1614–1619, 2008.
- Domenico Aquino, Alberto Bizzi, Marina Grisoli, Barbara Garavaglia, Maria Grazia Bruzzone, Nardo Nardocci, Mario Savoiardo, and Luisa Chi- apparini, “Age-related iron deposition in the basal ganglia: quantitative analysis in healthy subjects,” Radiology, vol. 252, no. 1, pp. 165–172, 2009.
- Martina F Callaghan, Patrick Freund, Bogdan Draganski, Elaine An- derson, Marinella Cappelletti, Rumana Chowdhury, Joern Diedrich- sen, Thomas HB FitzGerald, Peter Smittenaar, Gunther Helms, et al., “Widespread age-related dierences in the human brain microstructure re- vealed by quantitative magnetic resonance imaging,” Neurobiology of aging, vol. 35, no. 8, pp. 1862–1872, 2014.
- Huang, Chuan, et al. "T2 mapping from highly undersampled data by reconstruction of principal component coefficient maps using compressed sensing." Magnetic resonance in medicine 67.5 (2012): 1355-1366.
- Tamir, Jonathan I., et al. "T2 shuffling: sharp, multicontrast, volumetric fast spin‐echo imaging." Magnetic resonance in medicine 77.1 (2017): 180-195.
- Ong, Frank, Joseph Y. Cheng, and Michael Lustig. "General phase regularized reconstruction using phase cycling." Magnetic resonance in medicine 80.1 (2018): 112-125.
- Huang, Shuai, et al. "Fast Nonconvex $ T_2^* $ Mapping Using ADMM." arXiv preprint arXiv:2008.01806 (2020).
- Levine, Evan, et al. "3D Cartesian MRI with compressed sensing and variable view sharing using complementary poisson‐disc sampling." Magnetic resonance in medicine 77.5 (2017): 1774-1785.
- Boyd, Stephen, Neal Parikh, and Eric Chu. Distributed optimization and statistical learning via the alternating direction method of multipliers. Now Publishers Inc, 2011.
- Uecker, Martin, et al. "ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA." Magnetic resonance in medicine 71.3 (2014): 990-1001.
- Uecker, Martin, et al. "The BART toolbox for computational magnetic resonance imaging." ISMRM: Concord, CA, USA (2016).
- Wang, Yi, and Tian Liu. "Quantitative susceptibility mapping (QSM): decoding MRI data for a tissue magnetic biomarker." Magnetic resonance in medicine 73.1 (2015): 82-101.
Figures
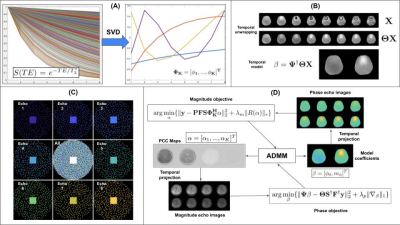
Figure 1. (A) Formation of magnitude temporal subspace basis from randomly generated T2* decay curves; (B) Two parameter phase temporal model; (C) Illustration of simultaneous spatial and temporal complementarity of COSTS sampling patterns; (D) Magnitude and phase objective functions used for reconstruction from undersampled k-space data
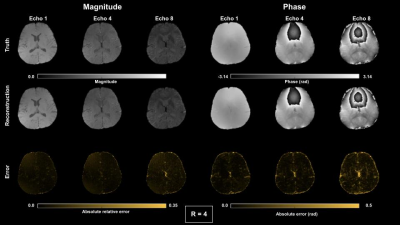
Figure 2. Magnitude and phase results for complex multi-echo reconstruction for echoes 1,4 and 8 using R = 4 COSTS undersampling.
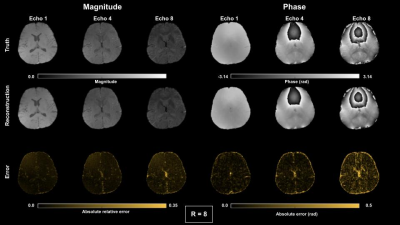
Figure 2. Magnitude and phase results for complex multi-echo reconstruction for echoes 1,4 and 8 using R = 8 COSTS undersampling.
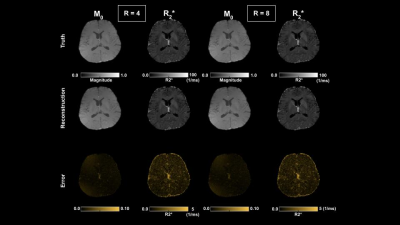
Figure 4. M0 and R2* results for R = 4 and 8.
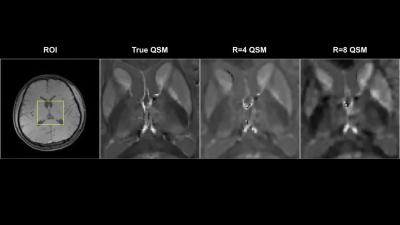
QSM results for a mid-axial slice for fully sampled data vs. R = 4,8.
DOI: https://doi.org/10.58530/2022/2349