2346
Model-based Image Reconstruction in Looping-star MRI1Electrical Engineering and Computer Science, University of Michigan, Ann Arbor, Ann Arbor, MI, United States, 2Biomedical Engineering, University of Michigan, Ann Arbor, Ann Arbor, MI, United States
Synopsis
Looping star is a silent MRI pulse sequence that can be used for quantitative susceptibility mapping (QSM), T2*-weighted imaging and fMRI. The conventional reconstruction approach for looping star MRI that filters out some the k-space data does not fully model the overlapping echoes, and remove potentially useful signals. This work proposes a model-based reconstruction method that can theoretically resolve the overlapping echos and improve the SNR without increasing the scan time.
Introduction
Loud acoustic noise in MRI can cause patient discomfort and anxiety, especially for certain groups of individuals like children or patients with dementia. Furthermore, in fMRI studies, acoustic noise is an additional confounding sensory stimulus, and can impact the blood-oxygen level dependent (BOLD) response as a function of both its loudness [1] and duration [2].Looping-star [3] is a silent MRI pulse sequence that can be used for quantitative susceptibility mapping (QSM), T2*-weighted imaging and fMRI. It is silent due to the slow-varying gradient, but it also suffers from low SNR and overlapping-echoes due to the burst RF pulses and looping k-space trajectory. Conventional reconstruction approach either trim the k-space to reduce overlapping artifact or use RF phase cycling which doubles the volume TR and make it infeasible for fMRI.In this work, we present a model-based reconstruction method that can resolve the overlapping-echoes and increase the SNR without increasing the scan time.
Methods
Pulse Sequence: Figure 1 shows a typical 2D looping star pulse sequence, consisting of a burst excitation and free induction decay (FID) module and one or more gradient echo (GRE) data acquisition module(s). The FID module has multiple short hard RF pulses that excite multiple k-space trajectories. With the same slowing varying gradient among modules, the k-space trajectories loops through the same circle in k-space for all modules.Problem Formulation: In looping-star fMRI, assuming we have $$$n_\text{spk}$$$ RF pulses in the FID module and following GRE module(s), there will be up to $$$n_\text{spk}$$$ k-space trajectories, each corresponding to a short hard RF pulses. Therefore, the signal sampled at any time $$$t$$$, denoted by $$$s_t$$$, is a superposition of $$$n_\text{spk}$$$ k-space samples located on corresponding trajectories. The corresponding signal equation of $$$j$$$th receiver coil with sensitivity map is given by [4]
$$s_t(j) = \int c_j(r) f(r) \sum_1^L e^{z(r) t_l} e^{-i 2\pi k(r) \cdot t_l} d r,$$
where $$$c_j(r)$$$ is the sensitivity map of $$$j$$$th receiver coil, $$$f(r)$$$ is the continuous proton density weighted object, $$$z(r) = \frac{1}{T2^*} + i \Delta B0(r)$$$ is the "rate map", and $$$L$$$ is the number of RF pulses that has been applied before time $$$t$$$.
Theoretically, the sampled signal model is the sum of signals from all those spokes. But in practice, 2 out of the $$$n_\text{spk}$$$ signals are located at low-frequency k-space, namely 'echo-in' and 'echo-out' signal, are at least 3 order of magnitude larger than others signals. So in the signal model, only 'echo-in' and 'echo out' spokes are included. Figure 2 shows simulated signals from a 2D Shepp-Logan phantom simulation and how 'echo-in' and 'echo-out' spokes are overlapping in time domain.
After discretization, we build the final system matrix as
$$ A = A_1 + A_2,$$
where each element of the $$$l$$$th sub-system matrix is $$$ a_{jil} = \sum_{j=1}^J \sum_{i=1}^{\text{res}} c_j(r_i) f(r_i) e^{z(r_i) t_l} e^{-i 2\pi k(r_i) \cdot t_l} $$$.
With the combined system matrix, we used conjugate gradient method for iterative image construction to optimize the following cost function
$$\hat{x} = \mathop{\mathrm{arg \,min}}_x \| y - A x \|_2^2 + \beta R(x),$$
where $$$R(x) = \| x \|_2^2$$$ here is a quadratic regularizer.
Compared to the conventional reconstruction method using k-space windowing to mitigate the overlapping echoes or RF phase cycling, the model-based approach can theoretically model and resolve the overlapping echoes, thus reducing the artifacts without increasing the scan time. The model-based approach uses echo-in and echo-out k-space information in higher k-space, thus improving the spatial resolution as well.
Experiments: We compare the proposed reconstruction method to the gridding reconstruction with 3D inverse Fourier transform (IFT) in a structured phantom and human study. We also designed a finger-tapping fMRI test with alternating 20s tapping and 20s resting. The model-based reconstruction using non-uniform Fourier transform and sensitivity map is called MB-v1, and overlapping-echoes resolved reconstruction is called MB-v2. The sequences were programmed via TOPPE [5] and implemented on a GE MR750 3.0T scanner with a Nova Medical 32RX head coil. Subjects gave informed consent under local IRB approval.
Results
Figure 3 shows the reconstruction of a structured phantom using gridding and model-based approach. Compared to the conventional gridding and Fermi filter approach, it is clear that the proposed MB-v2 has reduced artifacts.Figure 4 shows 4 slices of a human brain reconstruction versus different k-space radius. The model-based method outperforms the gridding method at all times. The case with full k-space data shows that the model-based approach can fully resolve the k-space overlapping echo and reduce artifacts. The fully model-based method with sensitivity map also allows for better suppression of undersampling artifacts than the gridding method.
Figure 5 shows a fMRI time courses and activation maps. The activation map using proposed MB-v2 has less noise and higher correlation coefficients. The time course also fits the reference better with less noise.
Conclusion
The proposed model based reconstruction showed better image quality on both phantom and brain study, and higher correlation coefficients and less noise in fMRI study. For further study, field inhomogeneity can be incorporated into the signal model and joint reconstruction of FID and GRE signals can also be explored.Acknowledgements
This work is supported in part by NIH Grants R01 EB023618.References
[1] Tomasi, Dardo, et al. "fMRI-acoustic noise alters brain activation during working memory tasks." Neuroimage 27.2 (2005): 377-386.
[2] Talavage, Thomas M., et al. "Quantitative assessment of auditory cortex responses induced by imager acoustic noise." Human brain mapping 7.2 (1999): 79-88.
[3] Dionisio‐Parra, Beatriz, et al. "Looping star fMRI in cognitive tasks and resting state." Journal of Magnetic Resonance Imaging 52.3 (2020): 739-751.
[4] Fessler, Jeffrey A. "Model-based image reconstruction for MRI." IEEE signal processing magazine 27.4 (2010): 81-89.
[5] Nielsen JF, Noll DC. TOPPE: A framework for rapid prototyping of MR pulse sequences. Magnetic resonance in medicine. 2018 Jun;79(6):3128-34.
Figures
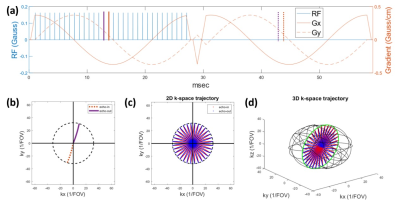
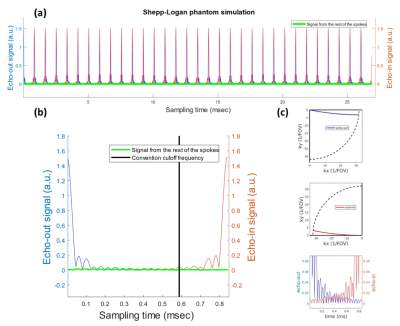
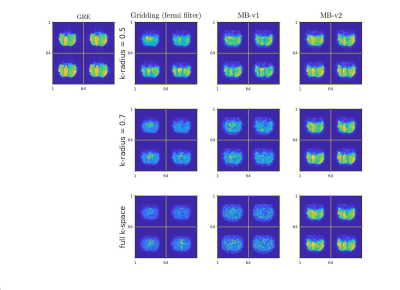
Figure 3: left to right: standard 3D gradient echo pulse sequence gridding reconstruction (scan time: 1:54 min), looping star (scan time = 1.9 s) gridding recon (with Fermi filter), looping star model-based reconstruction MB-v1, and looping star model-based reconstruction MB-v2.
First row: k-space data is trimmed to 0.5 of the maximum to remove most of overlapping artifacts at the cost of losing high-frequency signals. Second row: k-space data is trimmed to 0.7 of the maximum to reduce overlapping artifacts. Third row: full k-space data that has complete overlapping artifacts.
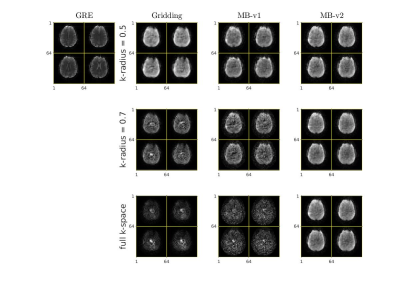
Figure 4: Reconstruction of brain: standard 3D GRE (scan time: 1:54 min) images for reference; All other images are from the same looping-star sequence (scan time = 1.9 s).
First, second and third rows show different reconstruction method using 0.5 of k-space data, 0.7 of k-space data, and full k-space data respectively. The proposed MB-v2 is robust to different range of k-space radius. It also produces higher quality images and could allow more k-space to be used in the image reconstruction.
