2345
Multi-domain Neumann Network with Sensitivity maps for Parallel MRI Reconstruction1Biomedical Engineering, Hankuk University of Foreign Studies, Yongin-si, Gyeonggi-do, Korea, Republic of, 2Department of Electrical and Computer Engineering, Marquette University, Milwaukee, WI, United States
Synopsis
We performed parallel MRI reconstruction from under-sampled k-space data using the Multi-Domain Neumann Network with Sensitivity Maps. The Neumann network solves the inverse problem with recursive neural networks taking account into the forward model. We adapt the Neumann network with the coil sensitivity estimation and k-space data regurlaization to take account into MR physical models. Our proposed method shows uppressed image artifacts and enhanced spatial resolution compared with GRAPPA, U-Net and Neumann network.
Introduction
As high-field MR increases in the clinical field, there is an increasing need to reduce scan time. In order to reduce scan time, the parallel imaging (PI)1-2 technique has been widely used. However, it is challenging for conventional reconstruction methods to remove aliasing artifacts, particularly with a high acceleration factor such as 4 or 8. Recently, deep learning-based methods showed great promise in parallel MRI reconstruction when a high acceleration factor is used3-9. In particular, Neumann network10 outperformed standard unrolled network architectures such as MoDL8,11, by directly incorporating the forward model into the network optimization. In this study, we propose a Multi-Domain Neumann Network with Sensitivity Maps (MDNNSM) that takes account into both image-domain and k-space-domain denoising for Neumann network’s regularization block combined with coil sensitivity maps. By integrating k-space data regularization and coil sensitivity map estimation into the Neumann network, we achieved significant improvement in reconstruction quality compared with the standard Neumann network.Methods
Problem Formulation: In the Neumann network, the parallel MRI reconstruction problem is formulated as follows.$$\tilde{x}^{0} = \lambda F^{-1}y \quad (\text{Eq. 1})$$ $$\tilde{x}^{j+1} = (I - \lambda F^{-1}F)\tilde{x}^{j} - \lambda R(\tilde{x}^{j}), \quad \forall j = 1, ..., N \quad (\text{Eq. 2})$$$$\text{and}$$$$\hat{x} = \sum_{j=0}^N\tilde{x}^{j} \quad (\text{Eq. 3})$$Where $$$\tilde{x}^{j}$$$ is the output of the $$$j$$$-th iteration and $$$y$$$ is multi-coil under-sampled k-space. $$$F$$$ and $$$R$$$ denote forward operator (e.g., Fourier Transform (FT)), and regularization, respectively. $$$\lambda$$$ represents the balance parameter between data consistency and regularization term. The final output $$$\hat{x}$$$ of Neumann network is the summation of intermediate reconstructed results.
We adapt the Neumann network to utilize k-space data regularization and coil sensitivity map based on MR physics. First, we introduce the new forward model $$$A$$$ that takes account into coil sensitivity maps.$$A=M\circ F\circ S\quad (\text{Eq. 4})$$
Where $$$A$$$ is a forward operator consisting of sensitivity map multiplication $$$S$$$, and under-sampling mask operator $$$M$$$. We now plug the new forward model $$$A$$$ in Eq. 1 and 2 as following.$$\tilde{x}^{0} = \lambda A^{-1}y \quad (\text{Eq. 5})$$$$\tilde{x}^{j+1} = (I - \lambda A^{-1}A)\tilde{x}^{j} - \lambda R(\tilde{x}^{j};A), \quad \forall j = 1, ..., N \quad (\text{Eq. 6})$$
It is worth noting that $$$R$$$ depends on both image $$$\tilde{x}^{j}$$$ and forward model $$$A$$$ for multi-domain regularization.
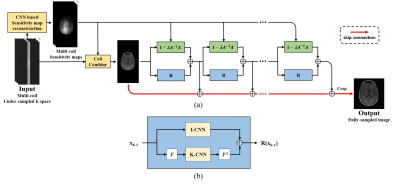
Network architecture: Fig. 1 illustrates the overall architecture of MDNNSM. The network consists of sensitivity map estimation block, data consistency block, regularization block, and skip connection. The sensitivity map estimation block reconstructs sensitivity maps using U-Net12 from the autocalibration signal (ACS) regions of multi-coil under-sampled k-space. The data consistency block measures the difference between the reconstructed image and the known k-space value using Neumann series expansion. The regularization block has two U-Nets that jointly denoise the reconstruction both in the image domain and the k-space domain. The output of each iteration is accumulated in the skip connection and comes out as the final output of the network.
Implementation details: We set the number of iteration blocks to 6 in the MDNNSM. The $$$\lambda$$$ was initialized to 1 all blocks. We used structural similarity (SSIM) loss function13 and ADAM optimizer for training our network, and the learning rate was 0.0001 and epochs was 50.
Experiments: We used a subset of the NYU fastMRI brain dataset14. The dataset consists of 3796 slices with 16-coil T1-weighted brain MRI. We used 2886 slices for training and 910 slices for validation, respectively. The k-space data were under-sampled using an equispaced sampling mask with acceleration factor 4 and 8. We compare our MDNNSM with the GRAPPA algorithm, U-Net, and Neumann networks.
Results
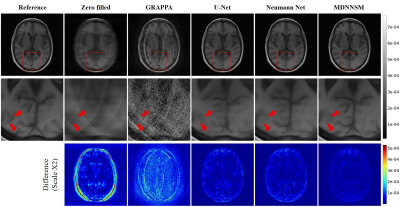
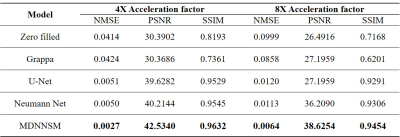
In Figure 2 and 3, we present the reference fully-sampled image and parallel MRI reconstruction images by various FFT-based and deep learning-based methods with acceleration factor 4 and 8, respectively. For both acceleration factors, our MDNNSM showed the improved reconstruction quality in terms of spatial resolution, noise level, and artifact reduction compared with other reconstruction methods as highlighted in zoomed and difference images. We note that only MDNNSM preserves the fine details of cortical surface in the fully-sampled reference image. (See the regions indicated by the red arrows in the zoomed image in Figure 2 and 3.) This indicates that multi-domain regularization with sensitivity maps enhances the Neumann network reconstruction.We also report quantitative evaluation scores for parallel MRI reconstruction with acceleration factor 4 and 8 in Table 1. Our proposed MDNNSM produces significantly lower NMSE and higher PSNR and SSIM than other reconstruction methods including the original Neumann network.
Conclusion
We proposed MDNNSM for parallel MRI reconstruction by incorporating multi-domain regularization and sensitivity map estimation into the Neumann network. Experimental results demonstrate that our MDNNSM shows the superior reconstruction quality compared with other FFT-based and deep learning-based parallel MRI reconstruction methods even including the original Neumann network.Acknowledgements
This research was supported by the MSIT (Ministry of Science, ICT), Korea, under the High-Potential Individuals Global Training Program (2021-0-01553) supervised by the IITP (Institute for Information & Communications Technology Planning & Evaluation).References
1. Pruessmann, K. P., Weiger, M., Scheidegger, M. B., & Boesiger, P. (1999). SENSE: sensitivity encoding for fast MRI. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 42(5), 952-962.
2. Griswold, M. A., Jakob, P. M., Heidemann, R. M., Nittka, M., Jellus, V., Wang, J., ... & Haase, A. (2002). Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 47(6), 1202-1210.
3. Han, Y., Sunwoo, L., & Ye, J. C. (2019). k-Space Deep Learning for Accelerated MRI. IEEE transactions on medical imaging, 39(2), 377-386.
4. Hammernik, K., Klatzer, T., Kobler, E., Recht, M. P., Sodickson, D. K., Pock, T., & Knoll, F. (2018). Learning a variational network for reconstruction of accelerated MRI data. Magnetic resonance in medicine, 79(6), 3055-3071.
5. Sriram, A., Zbontar, J., Murrell, T., Defazio, A., Zitnick, C. L., Yakubova, N., ... & Johnson, P. (2020, October). End-to-end variational networks for accelerated MRI reconstruction. In International Conference on Medical Image Computing and Computer-Assisted Intervention (pp. 64-73). Springer, Cham.
6. Eo, T., Jun, Y., Kim, T., Jang, J., Lee, H. J., & Hwang, D. (2018). KIKI‐net: cross‐domain convolutional neural networks for reconstructing undersampled magnetic resonance images. Magnetic resonance in medicine, 80(5), 2188-2201.
7. Schlemper, J., Caballero, J., Hajnal, J. V., Price, A. N., & Rueckert, D. (2017). A deep cascade of convolutional neural networks for dynamic MR image reconstruction. IEEE transactions on Medical Imaging, 37(2), 491-503.
8. Aggarwal, H. K., Mani, M. P., & Jacob, M. (2018). MoDL: Model-based deep learning architecture for inverse problems. IEEE transactions on medical imaging, 38(2), 394-405.
9. Jun, Y., Shin, H., Eo, T., & Hwang, D. (2021). Joint Deep Model-Based MR Image and Coil Sensitivity Reconstruction Network (Joint-ICNet) for Fast MRI. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 5270-5279).
10. Gilton, D., Ongie, G., & Willett, R. (2019). Neumann networks for linear inverse problems in imaging. IEEE Transactions on Computational Imaging, 6, 328-343.
11. Ongie, G., Gilton, D., & Willett, R. (2019, December). Learning to Solve Linear Inverse Problems in Imaging with Neumann Networks. In NeurIPS 2019 Workshop on Solving Inverse Problems with Deep Networks.
12. Ronneberger, O., Fischer, P., & Brox, T. (2015, October). U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical image computing and computer-assisted intervention (pp. 234-241). Springer, Cham.
13. Wang, Z., Bovik, A. C., Sheikh, H. R., & Simoncelli, E. P. (2004). Image quality assessment: from error visibility to structural similarity. IEEE transactions on image processing, 13(4), 600-612.
14. Zbontar, J., Knoll, F., Sriram, A., Murrell, T., Huang, Z., Muckley, M. J., ... & Lui, Y. W. (2018). fastMRI: An open dataset and benchmarks for accelerated MRI. arXiv preprint arXiv:1811.08839.
Figures