2344
g-CAMP reconstructs multiple b-value diffusion weighted images from a single RESOLVE k-space1Radiology and Biomedical Imaging, Yale School of Medicine, New Haven, CT, United States, 2Department of Biomedical Engineering, Yale University, New Haven, CT, United States
Synopsis
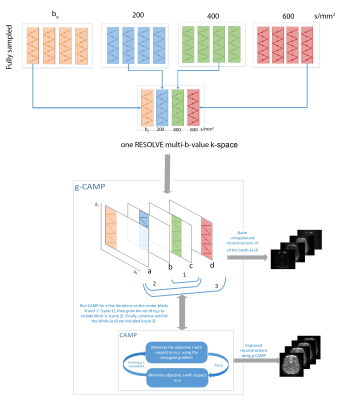
This work demonstrates the feasibility of reconstructing multiple b-value diffusion-weighted images (DWI) from a single RESOLVE k-space, where each blind was acquired with a different b-value. This multi b-value reconstruction uses the growing Constrained Alternating Minimization for Parameter mapping (g-CAMP) reconstruction method previously presented in ISMRM 2021. This can allow undersampling in the diffusion weighting dimension that is compatible with common undersampling schemes such as GRAPPA and multi-band EPI.
Introduction
Multiple b-values are important for improving the quality of DTI metrics. For example, computing DTI metrics from multi-shell data with b-values ranging from 300 s/mm2 to 2000 s/mm2 demonstrates more age associations than the single shell counterparts.1 However, since additional b-values require longer acquisition times, it may be useful to undersample in the multi-shell dimension2,3.We previously used g-CAMP4 (growing CAMP) to reconstruct quantitative T2-maps and a full T2w image series from a single Turbo Spin Echo (TSE) k-space, where each strip of k-space is acquired with a different T2 weighting. Similarly, g-CAMP can be applied to reconstruct the ADC map and full DWI series from a single k-space acquired from RESOLVE5,6 with just one blind acquired per b-value. The benefit of using RESOLVE is that it can provide higher resolution DWIs that are more immune to motion artifacts.
g-CAMP is based on the CAMP7,8 method, which alternates between optimizing the image series and the parameter map, and it does so by minimizing a single cost function that incorporates both (1) consistency between each individual parameter image and its k-space data and (2) adherence of the image series to the relaxometry model for each pixel. In g-CAMP, the standard CAMP method is applied first to the center two blinds. Then it grows in each direction until it includes all the blinds from the whole RESOLVE k-space.
Methods
CAMPThe CAMP objective function is defined as $$$J=J_1+J_2+J_3$$$ where $$$J_1$$$ is a data fidelity term, $$$J_2$$$ is a is a TV-norm regularization term, and $$$J_3$$$ is the CAMP constraint which captures the signal decay model. As previously described 8, exponential decay can be written as a linear relationship between subsequent images $$$m_{p+1} (x)=α(x)m_p (x)$$$, where $$$α(x)=exp(-p ∆b. ADC), $$$where $$$p$$$ is the number of b-values sampled, which also includes b0. Thus, the scaled CAMP constraint is $$$λ*∑_{(x=1)}^N∑_{(p=1)}^{(P-1)}‖m_{(p+1)} (x)-α(x)m_p (x)‖ ^2$$$. The CAMP objective function $$$J$$$ is alternately minimized with respect to $$$m_p$$$ (fixed $$$α$$$) using a non-linear conjugate-gradient method (Polak-Ribiere).9 It is then minimized with respect to $$$α$$$ (fixed $$$m_p$$$). This loop is repeated until both $$$m_p$$$ and $$$α$$$ converge.
g-CAMP
As shown in Figure 1, the g-CAMP algorithm starts by using only the two center blinds of k-space. A CAMP reconstruction on these two blinds continues for several iterations until it converges. Except for the middle two images, each image is initialized before entering the CAMP loop as a uniformly scaled version of the previously reconstructed neighboring image, using $$$α$$$ computed from the previous cycle. In addition, we forced each update to the $$$m_p$$$ series to be real.
Imaging
A RESOLVE sequence5,6 was acquired on a healthy volunteer. The diffusion images were acquired on a 3T MRI scanner (MAGNETOM Prismafit; Siemens Healthcare, Erlangen, Germany), using a 20-channel RF head coil. A RESOLVE sequence was acquired with five readout segments, TR=4000 ms, TE=82 ms for each blind, and TE= 144 ms for the navigators, with a base resolution of 160, 4 mm slice thickness. Monopolar diffusion scheme was used with b-values 0, 200, 400, 600 s/mm2, with one diffusion direction.
Processing
We preprocessed the raw data as described6 and then we divided each fully sampled image k-space into four blinds. In practice, an accelerated acquisition would acquire a single k-space like that shown in Figure.1, with a different b-value at each blind. Low-resolution phase priors could be calculated using a subset of k-space lines of the blind and the associated navigators, which are part of the RESOLVE sequence. The phase priors for each blind were incorporated as part of the encoding matrix. Finally, g-CAMP was applied to reconstruct four images, each with a different diffusion weighting, as well as an ADC map.
Results
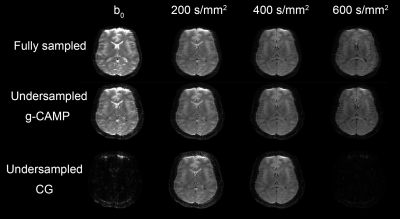
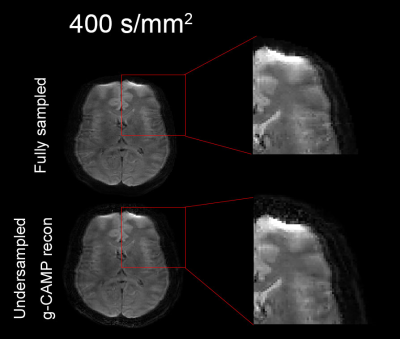
Figures.2 shows that g-CAMP could successfully reconstruct a high-fidelity ADC map from the undersampled data with only one blind at each b-value. Difference images between fully sampled ADC map and g-CAMP ADC counterpart show a normalized mean squared error (NRMSE) of 2.8 %. The bottom row of Figure.2 shows the reconstruction results of the conjugate gradient method for comparison. In addition, the rightmost column in Figure.2 shows a scatter plot of the fully sampled ADC map versus the g-CAMP reconstructed ADC map and versus the CG reconstructed ADC map. Figure.3 shows the full image series generated from the g-CAMP reconstruction, which, like the ADC maps, is in good agreement with the fully sampled reconstruction. An enlarged ROI from the DWI with 400 s/mm2 diffusion weighting (Figure.4) shows that resolution is well maintained.Discussion and Conclusion
This work demonstrates the potential of g-CAMP to reconstruct DWIs and quantitative ADC maps from a single RESOLVE k-space with a multi b-value acquisition. This method could allow for shorter scan time and high-resolution diffusion images with fewer motion artifacts. Multiple b-values are especially important for diffusion with nonlinear gradients, where additional images are typically needed to ensure each voxel is sampled at a reasonable range of b-values.10 g-CAMP is also fully compatible with diffusion encoding by nonlinear gradients, where multiple diffusion weightings are critical due to the spatially varying b-value. This method could be extended to include non-Gaussian models at higher diffusion weightings and additional directions for tractography.Acknowledgements
We note that both Dr. Galiana and Dr. Tagare contributed equally as senior authors on this work. This work was funded by the National Institutes of Health under R01CA264851, R01EB022030, and R21EB023414.References
1 Pines, A. R. et al. Leveraging multi-shell diffusion for studies of brain development in youth and young adulthood. Dev Cogn Neurosci 43, 100788, doi:10.1016/j.dcn.2020.100788 (2020).
2 Abascal, J. F. P. J., Desco, M. & Parra-Robles, J. Incorporation of Prior Knowledge of Signal Behavior Into the Reconstruction to Accelerate the Acquisition of Diffusion MRI Data. IEEE Transactions on Medical Imaging 37, 547-556, doi:10.1109/TMI.2017.2765281 (2018).
3 Liu, L., Johansson, A., Balter, J. M., Cao, Y. & Fessler, J. A. in 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018). 344-348.
4 Elsaid, N., Dispenza, N., Constable, R., Tagare, H. & Galiana, G. Quantitative T2 mapping from a single-contrast TSE scan using g-CAMP, ISMRM 2021.
5 Holdsworth, S. J. et al. Readout-segmented EPI for rapid high resolution diffusion imaging at 3T. European Journal of Radiology 65, 36-46, (2008).
6 Holdsworth, S. J., Skare, S., Newbould, R. D. & Bammer, R. Robust GRAPPA-accelerated diffusion-weighted readout-segmented (RS)-EPI. Magnetic resonance in medicine 62, 1629-1640, (2009).
7 Elsaid, N. M. H., Dispenza, N. L., Constable, R. T., Tagare, H. D. & Galiana, G. The impact of undersampling on the accuracy of the T2 maps reconstructed using CAMP ISMRM 2021.
8 Dispenza, N. L., Galiana, G., Peters, D. C., Constable, R. T. & Tagare, H. D. Accelerated R1 or R2 Mapping with Geometric Relationship Constrained Reconstruction Method. ISMRM 2019.
9 Polak, E. & Ribiere, G. Note sur la convergence de méthodes de directions conjuguées. ESAIM: Mathematical Modelling and Numerical Analysis - Modélisation Mathématique et Analyse Numérique 3, 35-43 (1969).
10 Hoque Bhuiyan, E., Dewdney, A., Weinreb, J. & Galiana, G. Feasibility of diffusion weighting with a local inside-out nonlinear gradient coil for prostate MRI. Medical Physics 48, 5804-5818, (2021).
Figures