Introduction

Fat is a confounding factor for EPI-based diffusion-weighted imaging (DWI)¹ due to the large chemical-shift effect. To overcome the imperfections of conventional fat-suppression techniques, chemical-shift encoding^2,3 has been recently proposed^4-6 to handle even multipeak fat spectra in EPI^5,6. Multi-shot EPI has gained growing popularity^7,8 in DWI to reduce geometric distortion, making motion-induced shot-to-shot phase errors correction via extra-navigated^7,8 or self-navigated^9-11 approaches necessary. However, when combined with chemical-shift encoding, the presence of shifted fat in the navigator signal can impair image reconstruction and degrade the quality of final water images. To circumvent such artefacts, we propose an extended model-based self-navigated water/fat decomposition resolved EPI (MSDE) image reconstruction algorithm to jointly estimate water and fat while correcting for the motion-induced shot-to-shot phase variations. The adverse effects of the shifted fat are successfully mitigated, and no extra navigator⁸ signal is required.

Methods

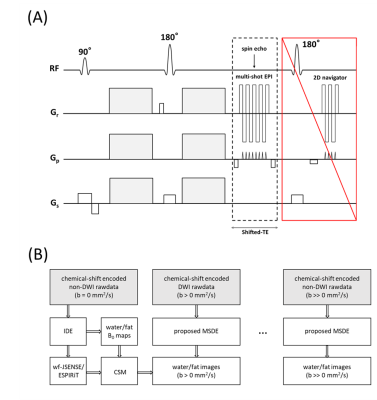
The DW signal model $$$s_{n,l,j}$$$ for a k-space sample $$$k_{t}$$$ at the $$$n$$$-th chemical-shift encoding point $$${\Delta}{{TE}_{n}}$$$, shot $$$l$$$ and coil $$$j$$$ can be written as:$$s_{n,l,j}(t)=\int\left[c_{j}(r)\rho_{w}(r)+\sum_{m=1}^{M}\alpha_{m}c_{j}(r)\rho_{f}(r)e^{i\psi_{f,m}\left({\Delta}{{TE}_{n}}+t\right)}\right]e^{i2\pi\psi_{B}(r){\Delta}{{TE}_{n}}}e^{i\phi_{n,l}(r)}e^{-ik_{t}r}dr\tag{1}$$where $$$\rho_{w}$$$ and $$$\rho_{f}$$$ denote the complex-valued water/fat components, $$$c_{j}$$$ the sensitivities, $$$\alpha_{m}$$$ and $$$\psi_{f,m}$$$ the relative amplitude and chemical-shift for each peak $$$m$$$ of the M-peak fat model, and $$$r$$$ the spatial position. $$$\psi_{B}$$$ is the B₀ inhomogeneity and $$$\phi_{n,l}$$$ the motion-induced phase, which are modulated in image-space avoiding the computational burden^12,13 imposed by equivalent k-space convolutions. The extended model-based water/fat separation can be solved with the conjugate gradient method (CG), by minimizing:$$\left\{P_{w},P_{f}\right\}=\underset{P_{w},P_{f}\in\mathbb{C}^{Q}}{\operatorname{argmin}}\|\hat{A}X-S\|_{2}^{2}\tag{2}$$where $$$Q$$$ is the number of voxels, $$$\hat{A}$$$ the coefficient matrix, $$$X=\left[P_{w},P_{f}\right]^{T}=\left[\rho_{w}^{1},\ldots,\rho_{w}^{Q},\rho_{f}^{1},\ldots,\rho_{f}^{Q}\right]^{T}$$$ the water/fat images, and $$$S$$$ the joint vectorized representation of all signals for $$$N$$$ chemical-shift encoding points, $$$L$$$ shots, and $$$J$$$ coils. The sequence and general reconstruction pipeline are illustrated in Figure 1. It is the aim to fully leverage all data sampled in a usual DWI scan. Thus, from chemical-shift encoded non-DWI measurements, a B₀ map, and water and fat threshold-based masks can be derived using an image-based water/fat decomposition approach for EPI (IDE)⁶. Furthermore, those non-DWI data are used to estimate coil-sensitivity maps (CSM) that match the EPI scan data conditions (geometric distortion). This is done by 1) using water-fat-JSENSE¹⁴, or 2) through ESPIRiT¹⁵ by performing water/fat separation for data acquired by each coil individually (with the estimated B₀ map from previous step) and estimating the merged water/fat (position-corrected) CSM.
For the diffusion measurements, a Gauss-Newton solver is implemented to jointly estimate water, fat and shot-to-shot phase maps. Using first-order Taylor expansion, the phase term error can be approximated as $$$e^{i\Delta\phi_{n,l}(\boldsymbol{r})}{\approx}1+i\Delta\phi_{n,l}(\boldsymbol{r})$$$ and updated for the next iteration. The number of iterations is empirically chosen to be 10. The unknown vector $$${\Delta}Y$$$ can be determined by minimizing,$$\left\{{\Delta}P_{w},{\Delta}P_{f},{\Delta}\Phi_{1,1},\ldots,\Delta\Phi_{N,1},\ldots,\Delta\Phi_{N,L}\right\}=\underset{\Delta\Phi_{n,l}\in\mathbb{R}^{Q}\atop{\Delta}P_{w},{\Delta}P_{f}\in\mathbb{C}^{Q}}{\operatorname{argmin}}\|\hat{B}{\Delta}Y-{\Delta}S\|_{2}^{2}\tag{3}$$where $$$\hat{B}$$$ is the coefficient matrix of the Gauss-Newton system, $$$\Delta\Phi_{n, l}=\left[\Delta\phi_{n,l}^{1},\ldots,\Delta\phi_{n,l}^{Q}\right]^{T}$$$ for $$$n=1,\ldots,N;l=1,\ldots,L$$$, and $$$\Delta{S}=S-\hat{A}\bar{X}$$$ with the current estimated $$$\bar{X}$$$. The pre-calculated water/fat masks are applied to the pre-estimated CSM to stabilize the estimation. To enforce smoothness of the estimated phase maps, a 2D triangular window¹⁴ (width set empirically to 5/6 of the matrix size) is applied in k-space for each Gauss-Newton iteration.
Experiments were conducted in head-neck regions and in the lower leg (4 subjects, 3T, Philips, Best, The Netherlands), using a spin-echo DW segmented EPI sequence with three b-values (0, 200, 400 s/mm²) or (0, 300, 600 s/mm²) sampling 4 or 6 interleaves at TE = 64 or 59 ms using 16-channel head-neck or 8-channel knee coil with TR=2000 ms at resolution: 1.4×1.5×4 mm³. The three $$${\Delta}{TE}$$$ were chosen as 0.2/ 1.0/ 1.8 ms with respect to the spin echo. For comparison, an extra 2D-navigator⁸ was acquired for each diffusion shot. A multi-peak fat model⁶ was used for all reconstructions.

Results

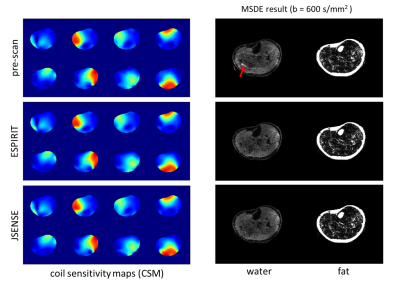
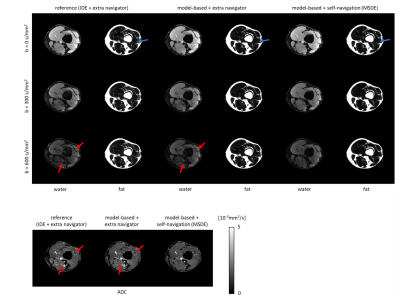
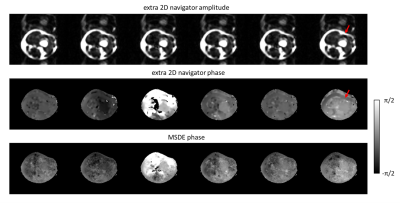
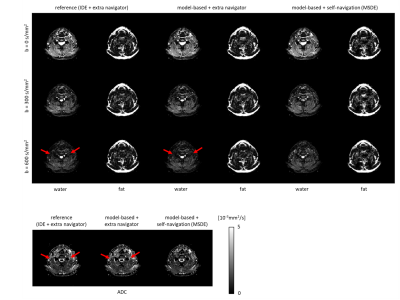
Figure 2 shows a DWI data set reconstructed using the proposed MSDE approach with the CSM obtained from SENSE pre-scan, ESPIRIT, and water-fat-JSENSE, respectively. The two approaches using self-calibrated CSM show improved water images compared to the one with the pre-scan. Figure 3 shows results of one subject’s leg, comparing IDE, the extended model-based water/fat separation with extra navigators, and the proposed self-navigated (MSDE). The artefacts shown in the water/ADC maps of the first two methods can be eliminated by using self-navigation. Figure 4 shows estimated phase maps from MSDE at one $$${\Delta}{TE}$$$ and the phase/magnitude of the extra navigators which contain shifted fat signal for comparison. Figure 5 shows the performance of the three approaches in the head-neck region. The examples show that the MSDE can avoid signal cancellations in the extra-navigated results.

Discussion and conclusion

The proposed MSDE algorithm provides more reliable water/fat separation for DWI compared to IDE. This is guaranteed by (1) the model-based reconstruction with fat off-resonance modulation in k-space, (2) the reduction of the spatial mismatch between CSM and EPI data, via integrated CSM estimation, (3) self-navigation to avoid measuring extra navigators which prolong acquisition times, suffer from poor SNR (acquired at TE > 100ms) and contain shifted fat signal, and (4) chemical-shift encoding, as an intelligent way of doing signal averaging, providing more data that help to better condition the inverse problem. This also supports the self-navigation to deal with the increased g-factor effects at large shots number.

Acknowledgements

The authors would like to acknowledge NWO-TTW (HTSM-17104).