Introduction

Various MRI methods require acquiring signal with either a long readout and/or a long TE (e.g., fMRI, multi-gradient echo sequences, etc.), allowing a long time for off-resonance precession to occur. In areas of relatively constant B0 field inhomogeneity, this precession impacts only the phase of the image. However, in voxels having large B0 gradients, spins within a single voxel can dephase with respect to each other, inducing signal loss in the reconstructed image.

Using model-based reconstruction to account for this intravoxel dephasing can help alleviate artifacts from this signal loss^1-3. However, in areas of severe signal loss such as near the sinuses, such reconstruction can fail to fully recover the image. Therefore, in this work we propose to combine model-based reconstruction with the use of a prephasing RF pulse so that the intravoxel spread of spins is approximately zero at the echo time, mitigating the associated signal loss. We incorporate the effects of this prephasing into a model-based reconstruction method and demonstrate improved reconstructed images.

Theory and Methods

Regularized model-based reconstruction for multi-channel data involves solving
$$\mathrm{arg min}_{\mathbf{x}} \sum_{c = 1}^C \frac{1}{2} \|\mathbf{A}_c \mathbf{x} - \mathbf{y}_c\|_2^2 + \lambda R(\mathbf{x}),\qquad (1)$$
where $$$\mathbf{x}$$$ is the image to recover, $$$\mathbf{y}_c$$$ is the k-space data from coil $$$c$$$, $$$\mathbf{A}_c$$$ is the system model mapping from image space to k-space for coil $$$c$$$, $$$C$$$ is the total number of coils, $$$R$$$ is a regularizer, and $$$\lambda$$$ is a tuning parameter. To account for intravoxel B0 effects and RF prephasing, $$$\mathbf{A}_c$$$ is given by
$$\mathbf{A}_c = (\mathbf{W} \odot \mathbf{F}) \mathbf{\Phi} \mathbf{S}_c \mathbf{x},\qquad (2)$$
where $$$\mathbf{S}_c$$$ is a diagonal matrix of coil sensitivity, $$$\mathbf{\Phi}$$$ is a diagonal matrix containing the bulk phase imparted to each voxel by the prephasing pulse, $$$\mathbf{F}$$$ is the Fourier operator, and $$$\odot$$$ is elementwise product. $$$\mathbf{W}$$$ is a matrix describing intravoxel dephasing effects with entries^3,4
$$W_{mn} = e^{-i2\pi f_n t_m} \mathrm{sinc}_3((\mathbf{k}_m + \mathbf{g}_n t_m + \mathbf{\gamma}_n) \odot \mathbf{\Delta}),\qquad (3)$$
where $$$n$$$ indexes spatial location, $$$m$$$ indexes k-space sample time, $$$f_n$$$ is the off-resonance frequency, $$$t_m$$$ is the k-space sample time, $$$\mathrm{sinc}_3$$$ is the 3D sinc function, $$$\mathbf{k}_m$$$ is the k-space location, $$$\mathbf{g}_n$$$ is the spatial gradient of the B0 field map, $$$\mathbf{\gamma}_n$$$ is the spatial gradient of the RF prephasing phase map, and $$$\mathbf{\Delta}$$$ is the voxel size. Note that $$$\mathbf{\Phi}$$$ and $$$\mathbf{\gamma}_n$$$ are the key new aspects that incorporate the effects of RF prephasing into the proposed model-based reconstruction method. An ideal RF prephasing pulse will impart phase such that $$$f_n \mathrm{TE} + \phi_n = 0$$$ (where $$$\phi_n$$$ is the $$$n$$$th diagonal entry of $$$\mathbf{\Phi}$$$) and an intravoxel spread of phase such that $$$\mathbf{g}_n \mathrm{TE} + \mathbf{\gamma}_n = \mathbf{0} \quad \forall n$$$; i.e., all spins throughout the object will be in phase at the echo time.

In this work, we compare model-based image reconstructions modeling intravoxel B0 effects with and without RF prephasing. We used the $$$\ell_2$$$-norm of 3D finite differences for the regularizer with $$$\lambda = 0.1$$$. We approximated $$$\mathbf{W}$$$ using a low-rank approximation³.

For the simulation experiments, we used a digital BrainWeb phantom⁵ and four synthetic coil sensitivity maps. We generated an off-resonance map with values 0–85 Hz and a spatial gradient with values -60–7.3 Hz/voxel (see Figure 1). We simulated a 64 × 64 × 3 matrix size Cartesian stack-of-EPI readout occurring from 3 to 40 ms with TE = 21.6 ms for each z phase encode. In one experiment, RF prephasing was specified such that all spins were in phase at the echo time. In another experiment, we varied the RF prephasing to rephase the spins at different times to investigate how RF prephasing accuracy can benefit reconstructed image quality.

Results

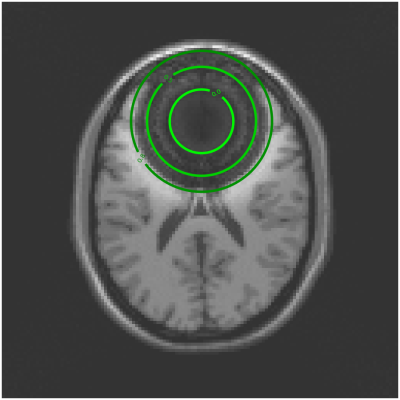
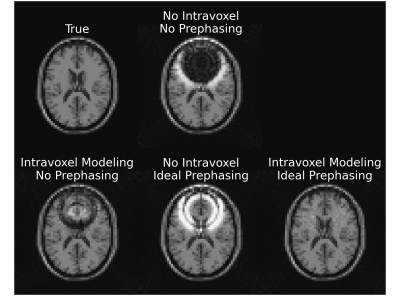
Figure 2 shows a reconstruction that does not account for intravoxel B0 effects. The overlayed contours draw a connection between the resultant signal loss and the corresponding value of the 3D sinc term in (3).

Figure 3 compares a reconstruction that does not account for intravoxel B0 effects to one that does, but without RF prephasing, and to one that includes both intravoxel B0 effects and RF prephasing. Each incremental addition to the model improves the reconstructed image, as verified by the normalized root mean square error (NRMSE) values reported in Table 1(a). Figure 3 also demonstrates that RF prephasing alone (without modeling intravoxel effects) is not enough to recover the true image, emphasizing the importance of the proposed reconstruction method.

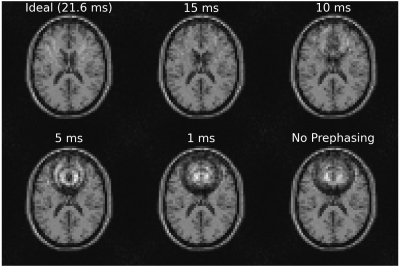
Figure 4 demonstrates what happens when the RF prephasing refocuses spins at different times. As expected, the closer to TE, the better, but there is still marked improvement even with refocusing occurring well before the echo time (e.g., when refocusing at 10 ms), as verified by the NRMSE values in Table 1(b).

Discussion and Conclusion

We introduced incorporating RF prephasing into model-based reconstruction including intravoxel B0 effects. The resultant reconstruction is better visually and in terms of NRMSE than when RF prephasing is not used in simulation.

Future areas of research include validating these simulation results with in vivo results, developing algorithms for designing RF prephasing pulses based on spectral⁶ and/or spatial^7,8 excitation profiles, and using the proposed method in an fMRI study to see how the fMRI activation maps are impacted.

Acknowledgements

This work was supported in part by NIH grants R21 AG061839 and U24 NS120056 and by NSF grant IIS 1838179.