2339
Iterative Model-Based Image Reconstruction of RF gradient-based MRI
Taylor Froelich1 and Michael Garwood1
1Center for Magnetic Resonance Research and Department of Radiology, University of Minnesota, Minneapolis, MN, United States
1Center for Magnetic Resonance Research and Department of Radiology, University of Minnesota, Minneapolis, MN, United States
Synopsis
When reconstructing with traditional Fourier-based techniques, image distortions arising from nonlinear B1 and B0 inhomogeneity can plague radiofrequency-based (RF) imaging methods that rely on B1 gradients for spatial encoding. In this work, we propose a new framework for reconstructing multi-dimensional RF gradient-based images leveraging an iterative approach to solve a regularized inverse problem. The proposed methodology employs a full Bloch simulation to reconstruct an undistorted image after determination of the forward operator and measured receive coil sensitivities.
Introduction
Recent advancements in radiofrequency imaging (RFI) utilizing B1 gradients to encode spatial information have shown the potential to produce images of equal or better quality than conventional MRI1. While there are distinct advantages to RFI-based methods, advanced reconstructions techniques must be employed to correct the image distortions caused by nonlinear B1 and B0 inhomogeneities. To overcome these distortions, we propose a new reconstruction technique based on an iterative approach utilizing a full Bloch simulation and receiver coil sensitivities.Methods
A recently developed RFI method called FREE (Frequency-modulated Rabi-Encoded Echoes)1 encodes spatial information in a manner resembling rotating frame zeugmatography2, except the magnetization rotates about a time-dependent effective field Beff(t) during an adiabatic sweep3,4. However, image distortions from nonlinear B1 and B0 inhomogeneity are observed in images acquired with FREE when Fourier-based image reconstruction is used.To overcome limitations in reconstruction, we propose utilizing an iterative first-order proximal gradient method to solve the regularized linear inverse problem of the form $$$||\mathbf{\mathit{Ax}}-\mathbf{\mathit{y}}||_{2}^2 + \lambda\Omega(\mathbf{\mathit{x}})$$$ where $$$\mathbf{\mathit{A}}$$$ represents the encoding matrix determined via full Bloch simulation with known field inhomogeneities and receive coil sensitivities5,6.
Initial in-vivo experiments were previously performed on a 1.5T, 90-cm Oxford magnet with a Siemens gradient system utilizing a multi- shot FREE double spin- echo (DSE) sequence1. Two phantom simulations were also performed with parameters comparable to previously acquired in-vivo data. These simulations focused on acceleration by under-sampling and the effect of performing FREE in a highly inhomogeneous B0 field with a constant linear gradient7. The first simulation considered FREE along two spatial dimensions with an acceleration factor of 4 and acquired on 8 separate receive channels. The latter considered the effect of a highly inhomogeneous static B0 field and a permanent linear B0 gradient producing 0.3 G/cm across a 5 cm FOV.
Results
A comparison between FFT-based and the proposed model-based reconstructions is shown in Fig. 1. FREE spatial encoding was performed with the surface coil’s (nonlinear) B1 gradient in the vertical (y-axis) direction, while conventional B0 frequency-encoding was used in the horizontal (x-axis) direction. Images depict the occipital lobes of a healthy subject. By including the B1 and B0 inhomogeneity in the forward model much of the image distortion was corrected using the proposed reconstruction approach.Fig. 2 shows a reconstruction created from a Bloch simulation of a 2-dimensional DSE FREE experiment, using identical surface coils along both dimensions. The data were acquired on 8 separate receive coils with an acceleration factor of 4 and complex white Gaussian noise added. By incorporating the B1 maps and receive coil sensitivity profiles into the forward model, the distortions are substantially removed and an alias free image is recovered.
Finally, an extreme example (Fig. 3) shows a reconstruction based on Bloch simulation of the DSE FREE experiment, using a surface coil for FREE (x-axis) and the calculated permanent B0 gradient (y-axis) generated from a passive shim set in a compact 1.5T head magnet. This result demonstrates that FREE, when combined with a permanent B0 gradient for frequency encoding, can generate good images with B1 and B0 maps included in the forward model.
Discussion
A primary limitation to model-based reconstruction is the need to accurately characterize the imaging system and address any mismatches between the encoding matrix and the physical experiment that can lead to artifacts in the reconstructed image. The latter can be challenging for some MRI methods that use B0 gradients for spatial encoding, since imperfections with pulsed B0 gradients (eg, eddy currents) can be more difficult to model8, whereas RF modulations typically have high fidelity. As such, RFI-based sequences that employ a B1 gradient to perform spatial encoding are highly predictable and reproducible. Moreover, the results herein show that at 1.5T a simple static Biot-Savart simulation is enough to adequately model the transmit coil profile. Incorporating this transmit profile into the encoding matrix led to significant improvement in the reconstructed image quality, especially compared to the traditional Fourier-based reconstruction. However at large distances from transmit coil, the object becomes heavily blurred as the strength of the B1 gradient decreases.When applied to accelerated FREE-based acquisitions with noise added, the proposed method reconstructs highly distorted, aliased images, while eliminating most of the artifacts. Despite these artifacts, the reconstructed image is significantly better than that of FFT-based methods. The reconstruction method was then applied to a simulation of an object in the presence of a highly inhomogeneous static B0 field and a nonlinear surface coil. The resulting Fourier reconstructed image is highly distorted along both dimensions due to the presence of the nonlinear fields. However, by incorporating these fields into the encoding matrix, the proposed reconstruction method was still able to produce images that are relatively distortion-free.
Conclusion
Standard Fourier based reconstruction has often produced artifacts when used in conjunction with RFI-based methods, limiting their adoption in clinical settings. However, the proposed reconstruction method presented here has shown that the artifacts can be eliminated and even enables accelerated acquisition. With these new tools, RFI-based imaging methods become more clinically viable and should ultimately produce comparable images to conventional acquisitions.Acknowledgements
This work was supported by the National Institutes of Health grants U01 EB025153 and P41 EB027061.References
1. Torres E, Froelich T, Wang P, DelaBarre L, Mullen M, Adriany G, Pizetta DC, Martins MJ, Vidoto ELG, Tannús A, Garwood M. B1-gradient–based MRI using frequency-modulated Rabi-encoded echoes. Magnetic Resonance in Medicine 2021:1-12.2. Hoult DI. Rotating frame zeugmatography. Journal of Magnetic Resonance (1969) 1979;33:183-197.
3. Garwood M, DelaBarre L. The return of the frequency sweep: Designing adiabatic pulses for contemporary NMR. J Magn Reson 2001;153:155-177.
4. Froelich T, Mullen M, Garwood M. MRI exploiting frequency-modulated pulses and their nonlinear phase. J Magn Reson 2020;318:106779.
5. Fessler JA. Optimization Methods for Magnetic Resonance Image Reconstruction. IEEE Signal Processing Magazine 2020:33-40.
6. Gutierrez A, Mullen M, Xiao D, Jang A, Froelich T, Garwood M, Haupt J. Reducing the Complexity of Model-Based MRI Reconstructions via Sparsification. IEEE Transactions on Medical Imaging 2021;40:2477-2486.
7. Kobayashi N, Parkinson B, Idiyatullin D, Adriany G, Theilenberg S, Juchem C, Garwood M. Development and validation of 3D MP-SSFP to enable MRI in inhomogeneous magnetic fields. Magnetic Resonance in Medicine 2021;85:831-844.
8. Barmet C, De Zanche N, Pruessmann KP. Spatiotemporal magnetic field monitoring for MR. Magn Reson Med 2008;60(1):187-197.
Figures
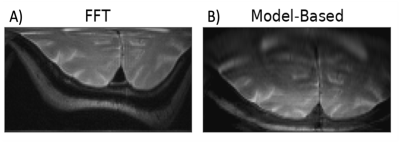
Figure 1: A comparison of reconstruction methods. These
images were acquired from a single surface coil placed 2.5 cm below the
imaged object, using 1D FREE (y-axis) combined with 1D frequency-encoding
(x-axis). The in-vivo image was acquired using the DSE FREE acquisition.
Model-based reconstruction removes much of the distortion caused by the
highly nonlinear B1 gradient of the surface transmitter coil. The
coil was positioned 2.5 cm posteriorly to the object.
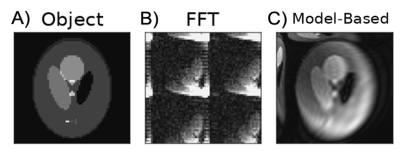
Figure 2:
Simulation of an accelerated 2D DSE
FREE sequence using two surface coils and 8 receive coils. The acquisition had
an acceleration factor of 4 and the transmit coils were placed on the left-hand
side and top of the object. Complex white Gaussian noise was added to the
simulated k-space data collected by each receive coil. Panel A) shows the
ground truth image used in simulations. Panels B) and C) show the standard FFT
reconstruction and the proposed model-based technique respectively.
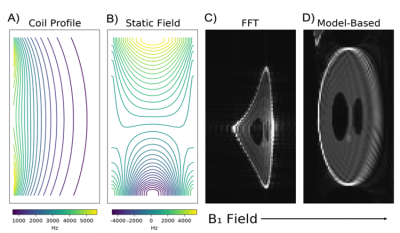
Figure 3:
Effect of a permanent B0 gradient
on a conventional DSE FREE sequence. Panel A) shows the nonlinear B1
gradient created by the surface coil placed on the left side, producing a
gradient mainly in the horizontal direction. Panel B) shows the static B0
inhomogeneity, including the permanent linear gradient mainly along the
vertical direction. The last two panels, C) and D), show a FFT reconstruction and the
proposed model-based technique, respectively. Distortion correction was
performed in post-processing by including the nonlinear B1 and B0
profiles into the forward model.
DOI: https://doi.org/10.58530/2022/2339