2284

Optimal Transport driven Cycle-consistent Generative Adversarial Network (OT-CycleGAN) for an accurate MR water-fat separation

Juan Pablo Meneses^1,2,3, Cristobal Arrieta^1,2, Gabriel della Maggiora^1,2, Pablo Irarrazaval^1,2,3,4, Cristian Tejos^1,2,3, Marcelo Andia^1,2,5, Sergio Uribe^1,2,5, and Carlos Sing Long^1,2,4,6,7
¹Biomedical Imaging Center, Pontificia Universidad Católica de Chile, Santiago, Chile, ²ANID – Millennium Science Initiative Program – Millennium Nucleus for Cardiovascular Magnetic Resonance, Santiago, Chile, ³Electrical Engineering, Pontificia Universidad Católica de Chile, Santiago, Chile, ⁴Institute for Biological and Medical Engineering, Pontificia Universidad Catolica de Chile, Santiago, Chile, ⁵Radiology Department, School of Medicine, Pontificia Universidad Catolica de Chile, Santiago, Chile, ⁶Institute for Mathematical & Computational Engineering, Pontificia Universidad Catolica de Chile, Santiago, Chile, ⁷ANID – Millennium Science Initiative Program – Millennium Nucleus for Discovery of Structure in Complex Data, Santiago, Chile

Synopsis

MRI water-fat separation is an ill-posed inverse problem usually addressed using complex numerical methods. This problem is related to an MR signal physical model that includes the effects of R₂^* signal decay ratio and main magnetic field inhomogeneities (Δf), which induce non-linearities that are related to the ill-posedness of the inverse problem. In this work, we propose an Optimal Transport driven Cycle-consistent Generative Adversarial Networks (OT-CycleGAN) framework, which is physics-based, and could use partially labeled training data to estimate the non-linear components (R₂^* and Δf), and posteriorly compute the water-fat images through a conventional least-squares approach.

Introduction

Non-Alcoholic Fatty Liver Disease (NAFLD) is a common condition worldwide, with an estimated global prevalence of 25%[1]. Liver fat fraction is the most relevant biomarker to diagnose this disease, and Proton Density Fat Fraction ($$$PDFF$$$$) is a highly correlated metric that could be measured non-invasively by solving the MR water-fat separation problem. However, to accurately solve it, a complex MR signal model should be considered, which include the multi-peak spectrum of fat[2], and the non-linear effects of $$$R_2^*$$$ signal decay and main magnetic field inhomogeneities ($$$\Delta f$$$). The current gold standard to solve this problem are iterative algorithms[3,4], although they show artifacts in some cases. Deep Learning (DL) methods have become a promising alternative due to their accuracy and artifact correction [5–7].
In this work, we propose an unsupervised DL approach based on an Optimal Transport driven Cycle-consistent Generative Adversarial Network (OT-CycleGAN)[8] to solve the non-linear component of the signal ($$$R_2^* , \Delta f$$$), and subsequently separate the water and fat signals through a linear least-squares estimation.

Methods

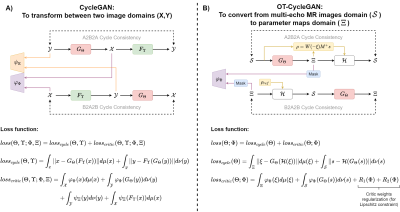
CycleGANs transform samples from one domain into another, using two pairs of neural networks: generator and critic[9]. Both models compete during the training process: while the generator tries to produce realistic synthetic data, the critic tries to discern between generated and real samples, assigning a score according to their verisimilitude. This competition is achieved by an iterative maximization/minimization of a loss function with cycle-consistency and critic terms (Figure 1A).
The forward problem is a deterministic physical model whose matrix formulation is defined as follows: $$\mathcal{H}: s(\rho,\xi)=W(\xi)M\rho$$
where $$$s$$$ is a vector with the complex MR signal at each echo, $$$W$$$ is a diagonal matrix that contains the non-linear effects of both $$$R_2^*$$$ and $$$\Delta f$$$ (summarized in the complex variable $$$\xi=\Delta f + i2\pi R_2^*$$$) evaluated at each echo time, $$$M$$$ is a matrix containing the spectral behavior of water and fat, and the $$$\rho$$$ vector contains water ($$$\rho_W$$$) and fat ($$$\rho_F$$$) signals.
Optimal transport theory allows for getting a physics-informed CycleGAN, which dispenses with a generator-critic pair and includes Eq.1 into the loss function (Figure 1B). The goal of the generator is to estimate receiving multi-echo images as input, for a posterior computation of the water-fat signals using the linear least-squares method: $$\rho=W(-\xi)M^+ s$$
Then, $$$PDFF$$$ can be estimated as the ratio of the water and fat signals: $$PDFF=\frac{|\rho_F|}{|\rho_W|+|\rho_F|}$$.

Experiments

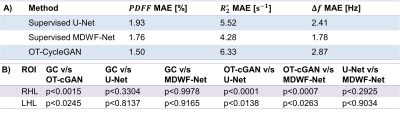
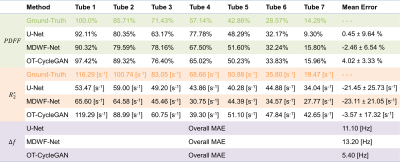
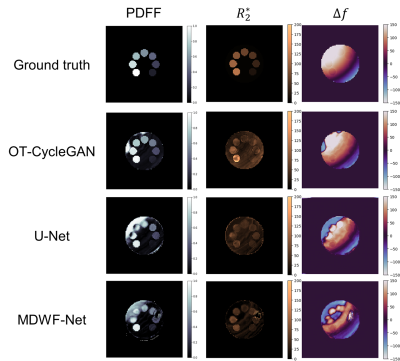
We considered six-echoes 2D multi-slice GRE acquisitions (TE₁/ΔTE/TR=1.3/2.1/30 ms) at 1.5T scanner (Achieva, Philips Healthcare) of 158 volunteers. The final database included 3545 slices, that were rescaled to 192x192 pixels by K-space subsampling. Since OT-CycleGAN can be trained using an unpaired dataset, we computed reference results for only 100 patients using Graph Cuts algorithm[4], which we considered as gold standard. The overall slices were divided into training (70%), validation (10%) and testing (20%) subsets.
For comparing with other DL approaches, supervised learning U-Net and MDWF-Net models were also trained[7]. Overall mean-absolute-error (MAE) with respect to Graph Cuts results was computed for $$$PDFF$$$, $$$R_2^*$$$ and $$$\Delta f$$$ maps. A one-way analysis of variance (ANOVA) followed by a Bonferroni post hoc test was also performed over $$$PDFF$$$ and $$$R_2^*$$$ estimations at specific liver ROIs (right posterior and left hepatic lobes, RHL and LHL respectively), considering a significance level of 0.05. To assess the ability of generalization, we also considered a simulated phantom that contained 7 tubes with different $$$PDFF$$$ (range: 14-100%) and $$$R_2^*$$$ (range: 19-116[s-1]) values and a $$$\Delta f$$$ map with a linear gradient (range: -300-300[Hz]).

Results

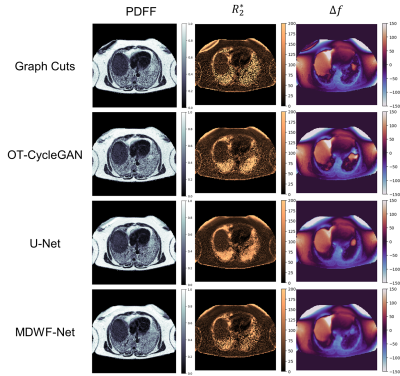
Supervised models showed lower $$$R_2^*$$$ and $$$\Delta f$$$ MAEs with respect to Graph Cuts than OT-CycleGAN. However, the latter displayed a lower $$$PDFF$$$ MAE. (Table 1A). One-way ANOVA showed significant differences for $$$R_2^*$$$ values at both RHL (p<0.0001) and LHL (p=0.0448). Particularly, Bonferroni post hoc test showed statistically significant differences between OT-CycleGAN and all the other methods (Table 1B). However, one-way ANOVA showed no significant differences for $$$PDFF$$$ estimations at RHL (p=0.997) and LHL (p=0.947). Qualitatively, $$$R_2^*$$$ maps were highly denoised compared to Graph Cuts results, and $$$\Delta f$$$ maps showed fewer swapping artifacts (Figure 2).
For the synthetic phantom (Figure 3), one-way ANOVA indicated no significant differences between all DL methods at $$$PDFF$$$ (p=0.9938) and $$$R_2^*$$$ (p=0.1996) estimations. However, OT-CycleGAN obtained a lower mean error and standard deviation for $$$R_2^*$$$, and a lower standard deviation for $$$PDFF$$$. For $$$\Delta f$$$ maps, OT-CycleGAN showed the lowest overall MAE (Table 2).

Discussion

OT-CycleGAN overperformed supervised models in $$$PDFF$$$ estimation. Nevertheless, only supervised models showed no significant differences to Graph Cuts in $$$R_2^*$$$ and $$$\Delta f$$$ estimations. However, a qualitative analysis of $$$R_2^*$$$ and $$$\Delta f$$$ suggested that supervised models could have replicated some Graph Cuts artifacts (noisy $$$R_2^*$$$, swaps in $$$\Delta f$$$) that were corrected by OT-CycleGAN.
Moreover, phantom’s results showed that OT-CycleGAN significantly overperformed the ability of generalization of supervised DL models.

Conclusion

OT-CycleGAN is a DL approach for the water-fat separation problem that could be trained with a partially labelled dataset and can achieve similarly accurate $$$PDFF$$$ estimations than the gold standard Graph Cuts algorithm. Moreover, due to its ability of generalization, OT-CycleGAN could be a more reliable alternative to use in clinical practice than other DL methods.

Acknowledgements

This work was funded by ANID – Millennium Science Initiative Program – NCN17_129. J.M. was funded by the National Agency for Research and Development (ANID) / Scholarship Program / DOCTORADO BECAS CHILE/2020 – 21210665. S.U. was funded by Fondecyt 1181057. C.T. was funded by Fondecyt 1191710, Anillo PIA ACT192064.

References

[1] J. Starekova, D. Hernando, P.J. Pickhardt, S.B. Reeder, Quantification of Liver Fat Content with CT and MRI: State of the Art, Radiology. (2021) 204288. https://doi.org/10.1148/radiol.2021204288.

[2] G. Hamilton, T. Yokoo, M. Bydder, I. Cruite, M.E. Schroeder, C.B. Sirlin, M.S. Middleton, In vivo characterization of the liver fat 1H MR spectrum, NMR Biomed. 24 (2011) 784–790. https://doi.org/10.1002/nbm.1622.

[3] S.B. Reeder, Z. Wen, H. Yu, A.R. Pineda, G.E. Gold, M. Markl, N.J. Pelc, Multicoil Dixon Chemical Species Separation with an Iterative Least-Squares Estimation Method, Magn. Reson. Med. 51 (2004) 35–45. https://doi.org/10.1002/mrm.10675.

[4] D. Hernando, P. Kellman, J.P. Haldar, Z.P. Liang, Robust water/fat separation in the presence of large field inhomogeneities using a graph cut algorithm, Magn. Reson. Med. 63 (2010) 79–90. https://doi.org/10.1002/mrm.22177.

[5] J.W. Goldfarb, J. Craft, J.J. Cao, Water–fat separation and parameter mapping in cardiac MRI via deep learning with a convolutional neural network, J. Magn. Reson. Imaging. 50 (2019) 655–665. https://doi.org/10.1002/jmri.26658.

[6] R. Jafari, P. Spincemaille, J. Zhang, T.D. Nguyen, X. Luo, J. Cho, D. Margolis, M.R. Prince, Y. Wang, Deep neural network for water/fat separation: Supervised training, unsupervised training, and no training, Magn. Reson. Med. (2021). https://doi.org/10.1002/mrm.28546.

[7] J.P. Meneses, C. Arrieta, G. della Maggiora, P. Irarrazaval, C. Tejos, M.E. Andia, C. Sing-Long, S. Uribe, Water/fat separation using multiple decoder U-Net architecture (MDWF-Net) for accurate R2* measurements, in: Proc. 29th Annu. Meet. ISMRM, 2021.

[8] B. Sim, G. Oh, J. Kim, C. Jung, J.C. Ye, Optimal Transport, CycleGAN, and Penalized LS for Unsupervised Learning in Inverse Problems, (2019) 1–25. http://arxiv.org/abs/1909.12116.

[9] J.-Y. Zhu, T. Park, P. Isola, A. Efros, Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks Jun-Yan, Proc. IEEE Int. Conf. Comput. Vis. (2017) 183–202. http://link.springer.com/10.1007/978-1-60327-005-2_13.

Figures

Figure 1: A) CycleGAN framework, consisting of 2 generators ($$$G_\Theta$$$, $$$F_\Upsilon$$$) and 2 critics ($$$\varphi_\Theta$$$, $$$\psi_\Xi$$$) that compete during training. B) Proposed OT-CycleGAN. An only generator ($$$G_\Theta$$$) estimates $$$\xi=\Delta f + i2\pi R_2^*$$$ that induce non-linear effects in the MR signal. An only critic ($$$\varphi_\Theta$$$) assess the verisimilitude of the $$$\xi$$$ samples. C) Architecture of generator and critic convolutional neural networks. Conv2D blocks of the critic included spectral normalization.

Table 1: A) Mean Absolute Errors (MAE), with respect to Graph Cuts, obtained with the testing set for $$$PDFF$$$, $$$R_2^*$$$ and $$$\Delta f$$$. The proposed OT-CycleGAN overperformed the supervised DL methods in $$$PDFF$$$ quantification, which is the metric of greatest interest. B) Bonferroni test p-values of $$$R_2^*$$$ estimations for each tested method for each considered ROI.

Figure 2: Example of $$$PDFF$$$, $$$R_2^*$$$ and $$$\Delta f$$$ quantification using each of the tested methods. The sample corresponded to a superior slice of the liver, in which the heart could also be observed. Swapping artifacts were observed near the chest, and noisy $$$R_2^*$$$ values were estimated in cavities.

Table 2: Mean errors obtained with each tested method at the synthetic phantom. $$$PDFF$$$ and $$$R_2^*$$$ estimations at each tube are displayed, in addition to the overall $$$\Delta f$$$ mean absolute error (MAE).

Figure 5: $$$PDFF$$$, $$$R_2^*$$$ and $$$\Delta f$$$ maps estimated using a simulated phantom. Unlike the proposed OT-CycleGAN, supervised DL models (U-Net, MDWF-Net) achieved a poor performance when tested over this phantom, especially in $$$R_2^*$$$ and $$$\Delta f$$$ quantification.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

2284

DOI: https://doi.org/10.58530/2022/2284