2257
Pycoilib: a free and pedagogical tool for the calculation of self/mutual inductance of coils of arbitrary geometry in python
Aimé Labbé1 and Marie Poirier-Quinot1
1Université Paris-Saclay, CEA, CNRS, Inserm, Laboratoire d'Imagerie Biomédicale Multimodale Paris Saclay, Orsay, France
1Université Paris-Saclay, CEA, CNRS, Inserm, Laboratoire d'Imagerie Biomédicale Multimodale Paris Saclay, Orsay, France
Synopsis
We introduce pycoilib, a python library developed for the computation of self and mutual inductance of coils. The library allows the user to design coils by dividing their three-dimensional geometry into collections of lines, arcs and circles, and by specifying the geometry of the cross-section of the coil wire. In a case study, the self-inductance of a deformable coil is computed as a function of its configuration. Pycoilib has the potential to become a valuable tool for prototyping, as well as teaching.
Introduction
Computing the self and mutual inductance of electrical circuits can be a tedious and daunting task. The equations involved in these calculation are difficult and usually don’t allow for an analytical solution even with the simplest geometries (e.g. a single loop). This led the literature to be filled with case specific approximations which can be difficult for newcomers to navigate1. The alternative is to use electromagnetic solvers, like COMSOL Multiphysics (Stockholm, Sweden), Sonnet (Syracuse, NY, USA) or FastHenry2 (Vimercate, MB, Italy): expensive and complex software. To fill the gap between these two approaches, we started developing a free and open python library pycoilib2, which lets the user draw a coil geometry (or a system of coils) using a predetermined set of segment shapes, and then computes the associated self/mutual inductance by solving integral representations of analytical equations. In this abstract, we recall the notion of inductance, we present the architecture of pycoilib, and we present a case study of a deformable coil.Self and mutual inductance
The idea behind pycoilib is to compute the inductance of a coil, neglecting propagation effects and assuming the high-frequency hypothesis (i.e. skin effect), by dividing its geometry into a collection of $$$N$$$ simple current segments and to compute the total inductance $$$I$$$ of the coil by using the following equation:$$$I = \sum_{p=1}^{N} I_p + 2 \sum_{p=1}^{N-1}\sum_{s=p+1}^{N}M_{p,s},$$$
where $$$I_p$$$ is the self inductance of segment $$$p$$$ and $$$M_{p,s}$$$ is the mutual inductance between segments $$$s$$$ and $$$p$$$. The mutual inductance $$$M_{s,p}$$$ can be calculated using the Neumann double integral formula:
$$$ M_{p,s} = \int_{\mathcal{C}_p} d\vec p \left( \frac{\mu_0}{4\pi} \int_{\mathcal{C}_s} \frac{d\vec s}{\| \vec p - \vec s\|}\right),$$$
where $$$\mathcal{C}_p$$$ and $$$\mathcal{C}_s$$$ are the paths along the primary and secondary segments, respectively. Eq. 2 corresponds to the integral over $$$\mathcal{C}_p$$$ of the magnetic vector potential induced by a unitary current flowing over $$$\mathcal{C}_s$$$. For the self-inductance $$$I_p$$$, then $$$\mathcal{C}_p$$$ and $$$\mathcal{C}_s$$$ correspond to the center and the edge of the wire.
Pycoilib architecture
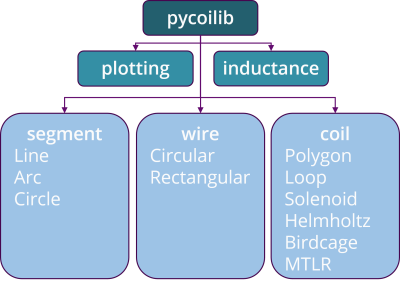
The architecture of pycoilib is displayed in Fig. 1 and was inspired by magpylib3¸ a magnetic field computation library in python. It consists of five modules. The segment module defines the list of available segment classes (Line, Arc, and Circle) and their parameterization (displayed in Fig. 2) . The wire module defines the wire classes (Circular and Rectangular) based of the cross-section of the wire. The coil module allows the construction of coil objects, which are defined as the association between a collection of segments (the coil geometry) and a wire object. This module also provides a list of subclasses for widely used coil designs such as solenoids, Helmholtz coils and birdcages. Then, the inductance module lists equations for the different pairs of segments. While some of the equations used in pycoilib were taken from the litterature4,5, several had to be solved. We found integral representation for these latter equations, and then validated them by comparing their computed outputs to the results of special cases found in Grover’s book1. Finally, a plotting module contains utility functions for the displaying of the coil object in three-dimension.Case study: a deformable coil
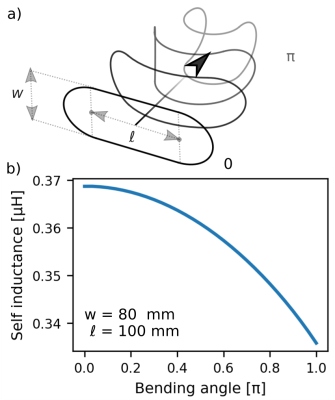
To showcase pycoilib, we present the example of a coil that is continuously deformed from a planar to a bent configuration, as displayed in Fig. 3a. This could model a flexible MRI coil being positioned on a patient to adopt the shape of a limb, for instance. The coil consists of a circular wire with radius 1 mm, and four segments: two lateral arcs of diameter $$$w=80$$$ mm linked by two lines of length $$$\ell=100$$$ mm, which become arc segments when the structure is bent. In Figure 3b, we display the computed self-inductance of the flexible coil for a bending angle from 0 to $$$\pi$$$. Small deformations ($$$<\pi/2$$$) have little impact on the self-inductance of the coil. However, for bending angles greater than $$$\pi/2$$$, the variation in self-inductance becomes significant, reaching 10 % for a bending angle of $$$\pi$$$. Considering a resonant frequency $$$f_0 = 1/(2\pi\sqrt{LC})$$$, with $$$C$$$ the capacitance of the circuit, this would entail a $$$\Delta f_0/f_0 \approx 5$$$ % variation of the coil frequency. If the coil quality factor $$$Q = f_0/\Delta f > f_0/\Delta f_0 = 20$$$, with $$$\Delta f$$$ the coil bandwidth, then the coil is untuned and will not effectively measure the MR signal.Discussion
Pycoilib is a python library that allows the user to design a coil and compute its inductance. It is meant to be free, easy to learn, simple to use, and can run on any computer with python installed. This makes pycoilib relevant for prototyping, as well as a good pedagogical tool for teachers and students alike. For MRI coil designers, pycoilib will not be as accurate as an electromagnetic solver. After all, propagation effects, which are important in high field applications, are unaccounted for in the library. However, for many applications where high precision is not critical, pycoilib can be a valuable tool.Conclusion
In this abstract, we introduced pycoilib, a free and open python library for coil design and inductance calculations. We described its architecture and then presented its use in the case of a flexible coil.Acknowledgements
This work was financially supported by the ANR (ANR-20-CE19-0027) and the LabEx LaSIPS (ANR-10-LABX-0032-LaSIPS) managed by the French National Research Agency as part of the "Investissements d'avenir" programme (ANR-11-IDEX-0003).References
1. Grover, F. W. (1964). Inductance calculations. New York: Dover.
2. Labbé, A. (2021). pycoilib. GitHub. Retrieved November 8, 2021, from https://github.com/ReciprocalSpace/pycoilib.
3. Ortner, M., & Bandeira, L. G. C. (2020). Magpylib: A free Python package for magnetic field computation. SoftwareX, 11, 100466.
4. Paul, C.R. (2011). Inductance: loop and partial. John Wiley & Sons.
5. Babic, S., Sirois, F., Akyel, C. and Girardi, C. (2010). Mutual inductance calculation between circular filaments arbitrarily positioned in space: alternative to grover's formula. IEEE transactions on magnetics, 46(9), pp.3591-3600.
Figures
Pycoilib architecture. Boxes represent
modules, and capitalized words represent classes.
Parameterization of (a) Line and (b) Arc classes in the segment module. The Circle class (not shown
here) is a subclass of Arc where $$$\varphi=2\pi$$$.
Deformable coil (a) geometry and (b) self-inductance as a function of the bending angle. The wire radius was set to 1 mm.
DOI: https://doi.org/10.58530/2022/2257