Introduction

MR Elastography (MRE) uses specialized motion encoding gradients (MEG) to encode tissue motion into the phase images^{1, 2}. Recently multi-frequency and transient MRE have been under intense study^3-8. For these applications the MEG needs to be carefully selected, and complicate deconvolution is needed for motion reconstruction^{3, 9-11}. The goal of this study was to image this broadband tissue motion with MEGs of multiple scales (multi-scale MRE) in the shape of a Haar wavelet series¹², which more efficiently encode broadband motion, and simplify the motion reconstruction into an inverse transform.

Theory

In MRE, the accumulated phase due to motion for each voxel is (eq.1):
$$\theta(t)=\frac{\gamma}{2\pi}\int_{0}^{t}\overrightarrow{G(\tau)}\cdot\overrightarrow{r(\tau)}d\tau \ \ \ [1] $$

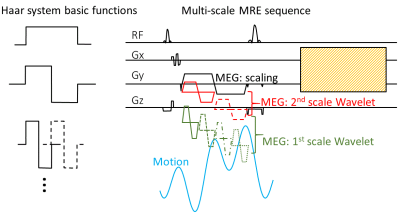
G(t) is the MEG and r(t) is the displacement. According to this equation, the phase is the cross-correlation between the tissue motion and the MEG. Therefore, if MEG is designed to approximate to a Haar series¹² (eq.2, Figure 1):
$$Scaling\ function:\varphi\left(t\right)=\begin{cases}1 & 0≤t<1\\0 & otherwise\end{cases} $$$$mother wavelet function: \psi(t)=\begin{cases}1 & 0\leq t<1/2\\-1 & 1/2\leq t<1\\0 & otherwise\end{cases} \ \ [2]$$ $$wavelet function: \psi_{j,k}(t)=\begin{cases}\sqrt{2}^{j} & \frac{k-1}{2^{j}}\leq t<\frac{k-1/2}{2^{j}}\\ -\sqrt{2}^{j} & \frac{k-1/2}{2^{j}}\leq t<\frac{k}{2^{j}}\\0 & otherwise\end{cases} $$
The accumulated phase would approximate the Haar transform of the motion (eq. 3):
$$a_0=\frac{1}{2^n}\int_{0}^{1}f\left(t\right)\varphi\left(t\right)dt$$
$$a_1=\frac{1}{2^n}\int_{0}^{1}f\left(t\right)\psi\left(t\right)dt \ \ \ \ [3]$$
$$a_{j,k}=\frac{1}{2^n}\int_{0}^{1}{f\left(t\right)\psi_{j,k}\left(t\right)dt}$$

Then displacement can be decoded using the inverse Haar transform (eq 4):
$$f_n\left(t\right)=a_0\varphi\left(t\right)+a_1\psi\left(t\right)+\sum_{2≤j≤n,\ 0≤k<2j-1}a_{j,k}ψ_{j,k}(t) \ \ \ \ [4]$$

Methods

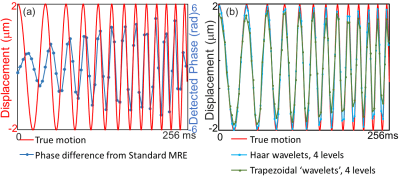
Figure 1 shows the diagram of a spin-echo-EPI-based MRE with multi-scale trapezoidal ‘Haar wavelet’ MEGs. In this figure two scales of wavelets and scaling function for two consecutive time windows is displayed (7 offsets). A single scaling function would crush the signal in MRI so a bipolar gradient that covered two consecutive time windows was used instead to encode the difference in a₀ between the two windows.
Firstly, a simulation verification was performed. A simulated true motion was defined to be a frequency sweep (20 Hz-80 Hz in 245.75 ms). This 245.75 ms interval was divided into 6 windows. Four wavelet scales plus scaling function were used to approximate the ‘true’ motion. Trapezoidal approximation of the wavelet series (slope length = 1ms) was simulated in addition to the rectangular theoretical Haar wavelet series. This was compared to a simulation performed with standard trapezoidal MEG of 60 Hz with a trigger delay of 4ms.
Secondly, a PVC phantom was scanned using both standard and a prototype multi-scale MRE sequence on a 3T scanner (MAGNETOM Skyra, Siemens Healthcare, Erlangen, Germany). A pneumatic driver (Resoundant Inc., Rochester MN, USA) generated the wave motion: (1) A composite continuous wave with 30Hz and 60Hz component having of equal amplitude, and (2) one cycle of 90-Hz sinusoidal wave (11 ms pulse length) per TR per slice. In multi-scale MRE a total 36 ms of motion were sampled, with 2 scales of wavelet in addition to the scaling function. MEG amplitude was 5mT/m for scaling and 2^nd scale wavelet, and 7mT/m for the 1^st wavelet. TR/TE=3200ms/47ms. With standard MRE 8 phase offsets were acquired, motion frequency=30 Hz, MEG frequency = 120 Hz, MEG amplitude = 40mT/m, and TR/TE=3200ms/35ms.
Lastly, a volunteer test was performed with multi-scale MRE using 1 scale of wavelets. Motion frequency=30 Hz, MEG amplitude=35mT/m and other parameters were the same were the same as for the phantom test.

Results

Figure 2 shows that motion within the simulated range can be detected by both standard and multi-scale MEG. With 4 scales of the Haar wavelets the reconstructed results followed the ‘true’ motion very well; With the trapezoidal ‘Haar wavelet’, the sensitivity decreased, especially when the frequency is higher, while the waveform was still preserved. The standard MEG is more sensitive to the frequency around 60 Hz and the phase response varied with the frequency.
In the composite wave test, both MRE techniques detected both frequency components. The standard MRE images showed more of the higher frequency component. The detected signal amplitude ratio of 60 Hz vs. 30 Hz was 1.38 with standard MRE and 0.44 in multi-scale MRE in the Y direction (the direction of the applied motion). Given that the standard 60-Hz MEG are 3.27 times as sensitive to 60 Hz as to 30 Hz, the composite wave imaging results from the two techniques were consistent. Stiffness calculated from the 30 Hz wave was 2.4 kPa with multi-scale MRE and 2.3 kPa with standard MRE, very close to each other.
Figure 4 shows the transient wave field caused by a single 90 Hz pulse in phantom. It can be observed that multiple frequency components are present in the phantom due to this pulse, and that standard MRE seemed to be more sensitive to the higher frequency component.
In the volunteer test, the 30 Hz wave images were reconstructed very well from multi-scale MRE (Figure 5).

Conclusions

The multi-scale MRE technique detected broadband motion with uniform frequency response hence better preserve the motion waveform. Phantom test results from multi-scale MRE and standard MRE were consistent. Multi-scale MRE is potentially useful to image transient or multi-frequency motion or motion with unknown frequency.

Acknowledgements

This work was supported by grant from National Institutes of Health R01 EB001981.