2244
2D or 3D MR elastography of the brain? Answers from a 1-year follow-up study in healthy volunteers.1Charité Universitätsmedizin Berlin, Berlin, Germany, 2Berlin Center for Advanced Neuroimaging, Berlin, Germany
Synopsis
MR elastography(MRE) measures in vivo soft-tissue mechanical parameters which are sensitive to various diseases. Robust and reliable measurements are critical for clinical translation; however, the variability of reported values, especially for MRE in the brain, remains a challenge. We here introduce an optimized setup for high-resolution brain MRE and compare the consistency of values obtained from 2D- and 3D-analysis in a group of healthy subjects studied in the follow-up of a year. Both 2D- and 3D-MRE values agreed very well between the two measurements. Intersubject variability was lower in 2D than in 3D while intrasubject variability was lower in 3D.
Introduction
Magnetic resonance elastography (MRE) is an emerging imaging modality which allows in vivo assessment of soft tissue mechanics.[1-3] In neuronal applications, MRE has been proven sensitive to disease and physiological effects both in 2D and 3D implementations.[4,5] An important step towards clinical applications of MRE of the brain is the evaluation of its consistency both in terms of inter- and intrasubject variability occurring over time due to potential technical and biological reasons. Although a relatively wide range of values is reported for brain tissue viscoelasticity[4,5], values should vary only slightly when the same MRE technique is used consistently. Efforts have been made to provide reference values in atlases of brain mechanics[6,7], as well as testing the inter- and intrasubject consistency of brain MRE based on 2D- or 3D-MRE with single or multiple frequency wave excitations.[8-12]This study has three aims: i) to introduce an optimized setup for high-resolution brain MRE based on multiple compressed air drivers, four mechanical frequencies and noise robust wave-number multifrequency inversion (k-MDEV), ii) to compare the consistency of values obtained from 2D- and 3D-k-MDEV and iii) to test whether MRE (2D or 3D) provides consistent brain stiffness values in healthy volunteers when re-measured in the follow-up of a year. Overall, we will address the question of whether 3D-MRE of the brain is beneficial compared with 2D-MRE.
Methods
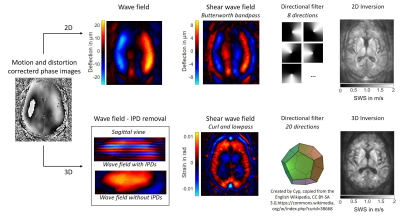
The brains of twelve healthy volunteers (mean±sd: 33±12years) were investigated by multifrequency MRE using a spin-echo echo-planar imaging sequence at a 3.0-Tesla scanner (Siemens-Lumina). Measurements were repeated after one year by a different operator. Eight phase offsets were recorded in 40 axial slices with 200x200mm2 field-of-view, 1.6x1.6x2mm3 voxel size, 70ms echo time and 4700ms repetition time. Harmonic vibrations at 20,25,35,40 Hz were induced using air drivers[13]. The average encoding efficiency was 8.4rad/µm with flow-compensated gradients.Raw data was corrected for motion and distortion using SPM12.[14] SWS maps were reconstructed using the phase-gradient based k-MDEV inversion[15] in 2D and 3D with brain adapted pre-processing[16-18]. For 2D, wave images were decomposed in eight propagation directions. Smoothing and suppression of compression waves was done using a bandpass Butterworth filter of third order with highpass threshold of 15/m and lowpass threshold of 250/m. For 3D, slice phase offsets and discontinuities had to be removed[19] from wave images. Shear wave fields were computed from the 3D curl of the wave images and decomposed in 20 three-dimensional propagation directions. Images were smoothed with a lowpass Butterworth filter of first order and threshold of 200/m. Data processing is visualized in Figure 1.
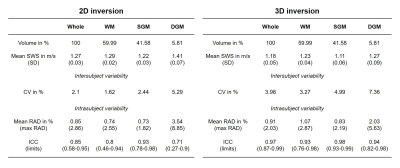
SWS maps were normalized to the MNI space for tissue segmentation[14] and averaged over whole brain, white matter (WM), subcortical gray matter (SGM) and deep gray matter (DGM). Averages were analyzed for intersubject variability by the coefficient of variation(CV) while intrasubject variability was analyzed by the relative absolute difference(RAD) and the intraclass correlation coefficient(ICC).[20-22]
Results
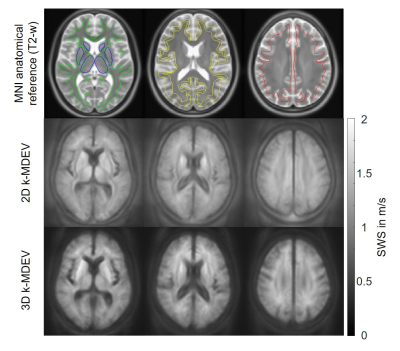
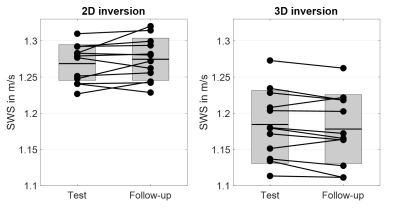
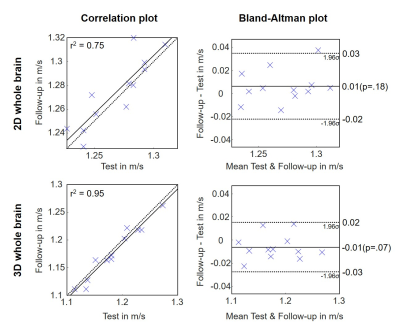
In Figure 2 group averaged SWS maps in MNI space are shown together with anatomical images. CSF spaces are slightly enlarged after 3D inversion.Test and follow-up results for both inversions for whole brain averages are presented in Figure 3. No significant aging effect was observed (whole brain; 2D: p=0.18, 3D: p=0.07). CV for whole brain in 2D and 3D was 2.1% vs 4.0%, while repeatability was better in 3D (whole brain; ICC: 0.85 vs 0.97). Smaller regions showed higher variations. Figure 4 presents the corresponding correlation and Bland-Altman plots[23]. Mean values were higher for 2D-k-MDEV (whole brain; 1.27±0.03m/s vs 1.18±0.05m/s,p<0.001). In both inversions DGM is stiffer than WM (2D: 10%,p<0.001, 3D: 4%,p=0.009) and WM is stiffer than SGM (2D: 6%,p<0.001, 3D: 11%,p<0.001). A summary of the results is given in Table 1.
Discussion and conclusion
To the best of our knowledge, this is the first study which compares stiffness of brain tissue in healthy subjects with a second measurement after one year. Additionally we compared 2D- and 3D-k-MDEV inversion in terms of region-averaged inter- and intrasubject variability. Importantly, 2D-MRE values were similar to 3D-values with slightly higher means in 2D. Intersubject variability over a year was lower in 2D than in 3D while intrasubject variability was lower in 3D than in 2D. Therefore, assuming that no biological variation of brain stiffness in our healthy subjects exists, we consider 2D-MRE more consistent than 3D-MRE. However, assuming that the higher intersubject variability seen in 3D-MRE represents a true biological variation and taking into account that the adult brain becomes softer over time (0.6% per year[24,25]), we see a trend in brain softening in 3D-MRE (~0.5%,p=0.07) which might reflect aging, and which is not seen in 2D-MRE. Thus, 2D-MRE might be better for detecting pathological changes against a narrow range of reference values with little intersubject variation, while 3D-MRE seems to be beneficial for individual changes in a longitudinal study design. More data and analysis are needed to substantiate these preliminary conclusions. A further argument pro-2D is the stability of inversion in boundary slices. In this study we excluded slices for avoiding thru plane derivate artifacts at slap edges, which is not necessary in a 2D study design. Nonetheless, it is encouraging that both 2D- and 3D-multifrequency SWS values agreed very well between the two measurements.Acknowledgements
Funding from the German Research Foundation (GRK 2260 BIOQIC, SFB1340 Matrix in Vision) and from the European Union’s Horizon 2020 Program (ID 668039, EU FORCE – Imaging the Force of Cancer) is gratefully acknowledged.References
[1] S.K. Venkatesh, R.L. Ehman, Magnetic resonance elastography of abdomen, Abdom Imaging 40(4) (2015) 745-59.
[2] Y. Jamin, J.K.R. Boult, J. Li, S. Popov, P. Garteiser, J.L. Ulloa, C. Cummings, G. Box, S.A. Eccles, C. Jones, J.C. Waterton, J.C. Bamber, R. Sinkus, S.P. Robinson, Exploring the biomechanical properties of brain malignancies and their pathologic determinants in vivo with magnetic resonance elastography, Cancer Res 75(7) (2015) 1216-1224.
[3] M.C. Murphy, J. Huston, 3rd, R.L. Ehman, MR elastography of the brain and its application in neurological diseases, Neuroimage 187 (2019) 176-183.
[4] Z. Yin, A.J. Romano, A. Manduca, R.L. Ehman, J. Huston, 3rd, Stiffness and Beyond: What MR Elastography Can Tell Us About Brain Structure and Function Under Physiologic and Pathologic Conditions, Top Magn Reson Imaging 27(5) (2018) 305-318.
[5] L.V. Hiscox, C.L. Johnson, E. Barnhill, M.D.J. McGarry, J. Huston, E.J.R. van Beek, J.M. Starr, N. Roberts, Magnetic resonance elastography (MRE) of the human brain: technique, findings and clinical applications, Physics in Medicine and Biology 61(24) (2016) R401-R437.
[6] L.V. Hiscox, M.D.J. McGarry, H. Schwarb, E.E.W. Van Houten, R.T. Pohlig, N. Roberts, G.R. Huesmann, A.Z. Burzynska, B.P. Sutton, C.H. Hillman, A.F. Kramer, N.J. Cohen, A.K. Barbey, K.D. Paulsen, C.L. Johnson, Standard-space atlas of the viscoelastic properties of the human brain, Hum Brain Mapp 41(18) (2020) 5282-5300.
[7] J. Guo, S. Hirsch, A. Fehlner, S. Papazoglou, M. Scheel, J. Braun, I. Sack, Towards an elastographic atlas of brain anatomy, PLoS One 8(8) (2013) e71807.
[8] S.F. Svensson, J. De Arcos, O.I. Darwish, J. Fraser-Green, T.H. Storås, S. Holm, E.O. Vik-Mo, R. Sinkus, K.E. Emblem, Robustness of MR Elastography in the Healthy Brain: Repeatability, Reliability, and Effect of Different Reconstruction Methods, J Magn Reson Imaging 53(5) (2021) 1510-1521.
[9] X. Huang, H. Chafi, K.L. Matthews, 2nd, O. Carmichael, T. Li, Q. Miao, S. Wang, G. Jia, Magnetic resonance elastography of the brain: A study of feasibility and reproducibility using an ergonomic pillow-like passive driver, Magn Reson Imaging 59 (2019) 68-76.
[10] A. Kolipaka, P.A. Wassenaar, S. Cha, W.M. Marashdeh, X. Mo, P. Kalra, B. Gans, B. Raterman, E. Bourekas, Magnetic resonance elastography to estimate brain stiffness: Measurement reproducibility and its estimate in pseudotumor cerebri patients, Clin Imaging 51 (2018) 114-122.
[11] C.L. Johnson, H. Schwarb, D.J.M. M, A.T. Anderson, G.R. Huesmann, B.P. Sutton, N.J. Cohen, Viscoelasticity of subcortical gray matter structures, Hum Brain Mapp 37(12) (2016) 4221-4233.
[12] M.C. Murphy, J. Huston, 3rd, C.R. Jack, Jr., K. Glaser, M.L. Senjem, J. Chen, A. Manduca, J. Felmlee, R.L. Ehman, Measuring the Characteristic Topography of Brain Stiffness with Magnetic Resonance Elastography, PLoS One 8(12) (2013) e81668.
[13] F. Schrank, C. Warmuth, H. Tzschätzsch, B. Kreft, S. Hirsch, J. Braun, T. Elgeti, I. Sack, Cardiac-gated steady-state multifrequency magnetic resonance elastography of the brain: Effect of cerebral arterial pulsation on brain viscoelasticity, Journal of Cerebral Blood Flow and Metabolism 40(5) (2020) 991-1001.
[14] W.D. Penny, K.J. Friston, J.T. Ashburner, S.J. Kiebel, T.E. Nichols, Statistical parametric mapping: the analysis of functional brain images, Elsevier2011.
[15] H. Tzschatzsch, J. Guo, F. Dittmann, S. Hirsch, E. Barnhill, K. Johrens, J. Braun, I. Sack, Tomoelastography by multifrequency wave number recovery from time-harmonic propagating shear waves, Med Image Anal 30 (2016) 1-10.
[16] H. Herthum, S.C.H. Dempsey, A. Samani, F. Schrank, M. Shahryari, C. Warmuth, H. Tzschatzsch, J. Braun, I. Sack, Superviscous properties of the in vivo brain at large scales, Acta Biomater 121 (2021) 393-404.
[17] H. Herthum, H. Tzschätzsch, T. Meyer, M. Shahryari, L. Stencel, J. Guo, J. Braun, I. Sack, Magnetic resonance elastography of the in vivo human brain using multifrequency wavenumber analysis in 2D and 3D., in: I.P.o.t.s.A.M.o. ISMRM (Ed.) ISMRM & SMRT Virtual Conference & Exhibition, 2021.
[18] H. Herthum, S. Hetzer, M. Scheel, M. Shahryari, J. Braun, F. Paul, I. Sack, In vivo stiffness of multiple sclerosis lesions is similar to that of normal-appearing white matter, Acta Biomaterialia (2021).
[19] E. Barnhill, M. Nikolova, C. Ariyurek, F. Dittmann, J. Braun, I. Sack, Fast Robust Dejitter and Interslice Discontinuity Removal in MRI Phase Acquisitions: Application to Magnetic Resonance Elastography, IEEE Trans Med Imaging 38(7) (2019) 1578-1587.
[20] B. Everitt, Encyclopedia of statistics in behavioral science, Wiley-Blackwell2005.
[21] J.M. Bland, D.G. Altman, Applying the right statistics: analyses of measurement studies, Ultrasound Obstet Gynecol 22(1) (2003) 85-93.
[22] M. Bédard, N.J. Martin, P. Krueger, K. Brazil, Assessing reproducibility of data obtained with instruments based on continuous measurements, Exp Aging Res 26(4) (2000) 353-65.
[23] R. Klein, Bland-Altman and Correlation Plot 2021. https://www.mathworks.com/matlabcentral/fileexchange/45049-bland-altman-and-correlation-plot. (Accessed November 7 2021).
[24] I. Sack, K.J. Streitberger, D. Krefting, F. Paul, J. Braun, The influence of physiological aging and atrophy on brain viscoelastic properties in humans, PlosOne 6(9) (2011) e23451.
[25] L.V. Hiscox, H. Schwarb, M.D.J. McGarry, C.L. Johnson, Aging brain mechanics: Progress and promise of magnetic resonance elastography, Neuroimage 232 (2021) 117889.
Figures