Introduction

Combined split-and-merge schemes for image segmentation have been introduced by Horowitz and Pavlidis¹ in the seventies of the last century. The principal idea of these region-based segmentation schemes is to recursively partition an image into small homogeneous parts and then to merge these small building blocks into larger homogeneous segments of the image. The merging step of these schemes is usually more cost intensive as the computational load required for the comparison and the combination of subregions is high. Therefore, a key aspect and at the same time also the challenge of split-and-merge strategies is to implement a splitting scheme that decomposes an image efficiently into a relatively small but geometrically significant number of subblocks (see Correa-Tome & Sanchez-Yanez² and Salembier & Garrido³). In this work, we will see that graph wedgelets⁴ form an interesting and promising tool for this geometric splitting part inside a split-and-merge segmentation procedure for Magnetic Resonance Imaging.

Materials and Methods

The wedge splitting procedure: to split the image into subregions that take into account the underlying geometry of the image we use a graph wedgelet decomposition as introduced in Erb⁴. Graph wedgelets interpret the image as a graph signal and efficiently approximate it with piecewise constant functions on partitions that are encoded in a binary graph partitioning tree and constructed upon hierarchical adaptive wedge splits. This structure allows to store and process the image partitions cost-efficiently by a sequence of graph nodes that encode the entire wedge partitioning tree. In Erb⁴, it was shown that with identical partition sizes graph wedgelets lead to a higher compression quality compared to quadtree decompositions or hierarchical Haar wavelet decompositions of images.
The merging procedure: once the image is decomposed into wedgelet subdomains, a merging scheme needs to be applied to the subdomains in order to obtain a segmentation of the image. For this, we proceed similarly as in Salembier & Garrido³ and generate a second binary partitioning tree for the merging step. For this merging partitioning tree a merging order and a region model is required. As a model for the image value on the union $$$R_1 \cup R_2$$$ of two regions $$$R_1$$$ and $$$R_2$$$ we use the median of the function values $$$F_1$$$ and $$$F_2$$$ on the subregions. The similarity between two regions $$$R_1$$$ and $$$R_2$$$ is measured by the quantity $$ O(R_1,R_2) = \min(N_1,N_2) (F_1 – F_2)^2,$$ where $$$N_1$$$ and $$$N_2$$$ denote the number of pixels in the respective subregions. According to this measure, the merging starts with those regions where the quantity $$$ O(R_1,R_2) $$$ is minimal. The merging scheme is completed and the image segmentation terminates if a selected partition size $$$K$$$ of composed subregions is reached.

Results and Discussion

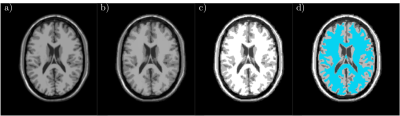
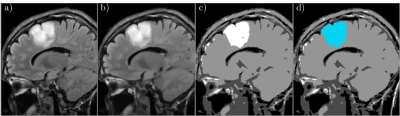
We test our scheme on two different MRI data sets. The first data set is an artificial MRI image of the brain (in Fig.1 a)) generated by the simulator BrainWeb (http://www.bic.mni.mcgill.ca/brainweb/). Using the presented split-and-merge approach, our goal is to segment the white matter from the rest of the surrounding brain tissue. Using the graph wedgelet algorithm, we split the original MRI image in 2500 subdomains (Fig.1 b), PSNR 33.19). Then, we apply the merging algorithm of Section 2 and obtain a segmentation of the image in terms of four different grayscales (Fig. 1 c)). The segment related to the white matter is afterwards colored in blue (Fig. 1 d)).
The second test image is an MRI scan containing a glioma (in Fig.2 a)) taken from a dataset on Kaggle (https://www.kaggle.com/sartajbhuvaji/brain-tumor-classification-mri/). The aim of this second experiment is to see whether our approach can segment the glioma from the rest of the image. Again, we conduct a wedgelet decomposition (Fig.2 b), PSNR 27.68) to split the image in 2500 subregions. After the application of the merging algorithm, we obtain a segmentation of the image in four grayscales (Fig. 2 c)). The segment describing the region with the glioma is colored in blue (Fig. 2 d)).
In both experiments, it is visible that the wedgelet algorithm provides a piecewise constant approximation of the original image and a splitting into a moderate number of geometrically significant wedge-shaped subregions. These preselected subregions can then be easily processed with the described merging method to obtain a simple and fast segmentation of the aimed-at regions. An advantage of the used wedgelet decomposition in the splitting procedure is that the original image is automatically denoised, leading to a more robust final segmentation. On the other hand, it is also visible that some details of the image get lost in those regions where the wedgelet approximation is not accurate enough. The wedgelet algorithm itself allows to select the number of adopted wedge splits, and, thus, to control the number of considered subregions and the accuracy of the wedgelet approximation. This trade-off between accuracy and robustness plays an important role also for the computational complexity of the method and needs to be investigated further to guarantee significant segmentations of medical MRI images. Furthermore, in this first study we used only a very simple model for the merging step. This leaves a lot of potential for further improvement.

Acknowledgements

Support of the Indam research group GNCS, the Italian Research Network on Approximation (RITA), and the research group on Approximation Theory and Applications of the Italian Mathematical Union (UMI-TAA) is gratefully acknowledged.