2104
Fiber coupling (FICO) measure using anisotropic smoothing of track orientation density images for tractogram filtering1A.I. Virtanen Institute for Molecular Sciences, University of Eastern Finland, Kuopio, Finland
Synopsis
Tractography is a powerful tool to study structural connectivity of the brain. However, its accuracy is known to be limited and tractograms are contaminated with large numbers of false positive streamlines. In this work, we propose a novel tractogram filtering approach. Our method leverages the topographic regularity of connections with which nearby streamline tend to follow similar trajectories. With this observation, we introduce an anisotropic smoothing approach for track orientation density images. These images are back projected onto the streamlines, which provides information about fiber-to-bundle coupling (FICO). Streamlines are then filtered by thresholding their FICO value.
Introduction
Diffusion MRI (dMRI) based tractography is a powerful, in vivo technique to study the structural connectivity of the brain. Tractography is highly useful, in particular for seed-based studies, where the focus is on connections projecting to/from a chosen seed region in the brain. For example, functional seeding based on transcranial magnetic stimulation (TMS) is used for investigating cortico-spinal-tract integrity, which helps neurosurgical planning [1,2]. On the other hand, tractography is well-known to have limited accuracy. It suffers from large amounts of false positive [3,4] and negative connections [5]. This has lead the researchers to investigate options to improve tractograms through various approaches such as streamline filtering [6,7,8]. In this work, we propose a novel tractogram filtering approach to reduce false positive streamlines. Our technique offers an effective solution without the need for pair-wise streamline comparison. Therefore, it can be used for filtering tractograms with large numbers of streamlines.Methods
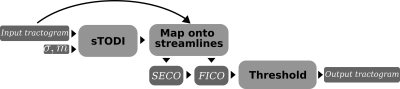
Our approach is based on thresholding anisotropically smoothed track orientation density images (TODI) [9]. By taking into account the orientational contributions of streamlines inside a voxel, TODI expands on the track-density imaging (TDI) approach [10]. With that, TODI expresses the total directional contribution of all streamlines passing through a voxel as a spherical function. In this work, we further expand on the TODI concept by injecting in the topographic regularity property of connections in the brain, which leads nearby streamlines to follow parallel trajectories to each other. Based on this, we propose an approach to generate anisotropically smoothed TODI (sTODI) images. In sTODI, we distribute the directional contribution of each streamline not only on the voxels they pass through but also on other voxels that are parallel to the streamline.Let $$$T=\{S_1,S_2,...S_n\}$$$ be a set that represents a tractogram, where $$$S_i=(p_{i1},p_{i2},...,p_{il})$$$ are streamlines, i.e., sequences of points, $$$p$$$. For each $$$S_i$$$, we create a set of $$$m$$$ parallel streamlines, that creates a larger tractogram, $$$T'=\{S_{11},...,S_{1m},S_{21},...,S_{2m},S_{n1},...,S_{nm}\}$$$. As shown in Fig. 1, we assume a Gaussian distribution for generating the parallel streamlines, where the standard deviation ($$$\sigma$$$) and the number ($$$m$$$) of parallel streamlines are user inputs. sTODI is then simply $$${sTODI}=TODI(T')$$$. In our implementation, parallel streamlines are generated only temporarily in the computer memory during sTODI computation.
With anisotropic smoothing, in each voxel, sTODI shows how well neighboring streamlines support the orientation of the overall fiber bundle. We then project this information back on each streamline by interpolating the sTODI values on each point along the streamlines based on the direction ($$$dir$$$) of the segments. We name this feature as segment(-to-bundle) coupling. SECO is a feature assigned for each point on a streamline and it shows show well the segments align with the bundle. Because SECO rapidly increases in dense regions of the tractogram, we use the logarithm, yielding $$$SECO_{ij}=log(sTODI(p_{ij},dir_{ij}))$$$ for the $$$j^{th}$$$ point on the $$$i^{th}$$$ streamline.
The minimum SECO value on a streamline is used to represent the fiber(-to-bundle) coupling (FICO), i.e. $$$FICO_i=min(SECO_{i1},SECO_{i2},…,SECO_{il})$$$. FICO is a scalar value assigned to each streamline and it represents how well a streamline aligns with the rest of the bundle. Fig. 2 shows the flow chart for the complete tractogram filtering approach, which is based on thresholding FICO.
Results
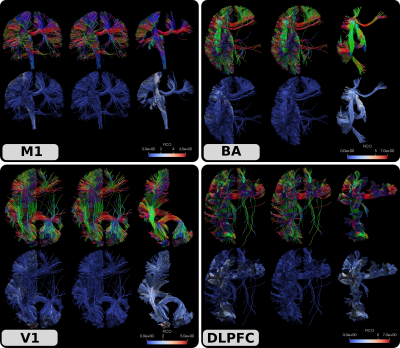
We demonstrated the results of our approach by simulating a TMS experiment on an HCP subject (ID: #100307) [11]. To that end, we first computed FOD images using the approach in [12] and generated 100 million streamlines using anatomically constraint tractography (ACT) [13] with the ptt algorithm [14] implemented in Trekker (https://dmritrekker.github.io/). The whole brain tractogram was then filtered using the SIFT algorithm [15] with Mrtrix [16] so that the final tractogram contained 10 million streamlines. We then manually picked 4 seed points from commonly used TMS targets: motor cortex (M1), Broca’s area (BA), visual cortex (V1) and dorso-lateral prefrontal cortex (DLPFC). We used Mrtrix’s tckedit command using the seed coordinates and extracted all the streamlines within a radius of 3 mm. Fig. 3. shows the input fiber bundles, FICO values and the output filtered tractograms.Discussions and conclusion
Despite the efforts of the tractography community over the few past decades, tractography is still not a mature enough tool to have wide-spread clinical applications. A major limitation is the clearly visible false positive connections that mostly dangle within the brain. The problem largely persists despite the application of existing filtering approaches. This can also be observed in Fig.3, where the input tractograms still contain large numbers of dangling streamlines despite the application of ACT and SIFT. To address this problem in an efficient manner, in this work we proposed FICO, a novel approach based on sTODI images. In our preliminary experiments, we demonstrated that our approach is fast and effective in reducing false positive streamlines. Because our primary focus is on TMS neuronavigation, in our preliminary experiments, we focused on visual evaluation using a single subject. Our future work will focus on expanding the experiments to also provide quantitative insight on the improvement in tractograms. A C/C++ implementation of the algorithm will be shared by the ISMRM meeting.
Acknowledgements
This work was in part supported by the Academy of Finland. Data used in this paper were provided in part by the Human ConnectomeProject, WU-Minn Consortium (Principal Investigators: David Van Essenand Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes andCenters that support the NIH Blueprint for Neuroscience Research; and bythe McDonnell Center for Systems Neuroscience at Washington University.References
[1] Lucas, Carolin Weiss, et al. "Functional MRI vs. navigated TMS to optimize M1 seed volume delineation for DTI tractography. A prospective study in patients with brain tumours adjacent to the corticospinal tract." NeuroImage: Clinical 13 (2017): 297-309.
[2] Fekonja, Lucius S., et al. "Detecting corticospinal tract impairment in tumor patients with fiber density and tensor-based metrics." Frontiers in oncology 10 (2020).
[3] Schilling, Kurt G., et al. "Limits to anatomical accuracy of diffusion tractography using modern approaches." NeuroImage 185 (2019): 1-11.
[4] Maier-Hein, Klaus H., et al. "The challenge of mapping the human connectome based on diffusion tractography." Nature communications 8.1 (2017): 1-13.
[5] Aydogan, Dogu Baran, et al. "When tractography meets tracer injections: a systematic study of trends and variation sources of diffusion-based connectivity." Brain Structure and Function 223.6 (2018): 2841-2858.
[6] Meesters, Stephan, et al. "Cleaning output of tractography via fiber to bundle coherence, a new open source implementation." Abstract. Presented at Organization for Human Brain Mapping Annual Meeting, Geneve, Switzerland. 2016.
[7] Wang, Junyan, et al. "Modeling topographic regularity in structural brain connectivity with application to tractogram filtering." Neuroimage 183 (2018): 87-98.
[8] Chandio, B. Q., et al. "FiberNeat: unsupervised streamline clustering and white matter tract filtering in latent space." (2021).
[9] Dhollander, Thijs, et al. "Track orientation density imaging (TODI) and track orientation distribution (TOD) based tractography." NeuroImage 94 (2014): 312-336.
[10] Calamante, Fernando, et al. "Track-density imaging (TDI): super-resolution white matter imaging using whole-brain track-density mapping." Neuroimage 53.4 (2010): 1233-1243.
[11] Van Essen, David C., et al. "The Human Connectome Project: a data acquisition perspective." Neuroimage 62.4 (2012): 2222-2231.
[12] Tran, Giang, and Yonggang Shi. "Fiber orientation and compartment parameter estimation from multi-shell diffusion imaging." IEEE transactions on medical imaging 34.11 (2015): 2320-2332.
[13] Smith, Robert E., et al. "Anatomically-constrained tractography: improved diffusion MRI streamlines tractography through effective use of anatomical information." Neuroimage 62.3 (2012): 1924-1938.
[14] Aydogan, Dogu Baran, and Yonggang Shi. "Parallel Transport Tractography." IEEE Transactions on Medical Imaging 40.2 (2020): 635-647.
[15] Smith, Robert E., et al. "SIFT: Spherical-deconvolution informed filtering of tractograms." Neuroimage 67 (2013): 298-312.
[16] Tournier, J-Donald, et al. "MRtrix3: A fast, flexible and open software framework for medical image processing and visualisation." Neuroimage 202 (2019): 116137.
Figures

Figure 1. To compute sTODI, for each streamline in the tractogram, parallel streamlines are generated. The figure shows an example for a single streamline shown on the left. Assuming a Gaussian distribution, we generate denser concentration of parallel streamlines near the input streamline. $$$\sigma$$$ and $$$m$$$ are user inputs and examples for different combinations are shown above. sTODI is simply TODI computed on the set of parallel streamlines.