2078
Super-Resolution for CEST MRI1Computer Science, Friedrich-Alexander Universität Erlangen-Nürnberg, Erlangen, Germany, 2Institute of Radiology, University Hospital Erlangen, Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Erlangen, Germany, 3Institute of Neuroradiology, University Hospital Erlangen, Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Erlangen, Germany, 4Department of Internal Medicine 3, University Hospital Erlangen, Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Erlangen, Germany, 5Magnetic Resonance Center, Max-Planck-Institute for Biological Cybernetics, Tübingen, Germany, 6Division of Medical Physics in Radiology, German Cancer Research Center (DKFZ), Heidelberg, Germany
Synopsis
The resolution of chemical exchange saturation transfer (CEST) magnetic resonance imaging is limited by physical constraints. To visualize metabolic processes of small structures using CEST in patients knees, an increased resolution is necessary. In this work, we compared trilinear interpolation and zero-filling to neural network-based approaches to estimate a high-resolution image given the corresponding low-resolution data. We could show that a substantial quantitative improvement using neural networks could be achieved for unsaturated images while maintaining a comparable CEST contrast. Generalization of the method to brain CEST MRI was achieved without retraining of the network.
Introduction
The resolution of magnetic resonance imaging (MRI) using chemical exchange saturation transfer (CEST) is limited by the signal-to-noise ratio [1]. For the application of CEST in a rheumatologic setting, imaging of thin structures such as the synovial tissue is challenging. Thus, CEST MRI with improved spatial resolution would be highly desirable. Previous neural network-based super-resolution work mostly focused on increasing the resolution of common MR sequences such as fast-spin-echo and double echo in steady-state [2,3], and was limited to specific regions of the human body such as the knee or the head [3,4]. We will show that neural networks are capable of generating high-resolution (HR) images from low-resolution (LR) input images leading to an increased resolution of the CEST contrast. Further, we will demonstrate the generalization of our method by the application of the trained network to CEST brain scans.Methods
Due to the difficulty to acquire HR CEST images, since the required longer readout trains would alter the contrast, for the training and quantitative evaluation unsaturated MR images of the knee were used. To generate LR inputs the k-space of the HR images was center-cropped by a factor of two. The network results were compared to k-space zero-filling with a Tukey filter window (filter was chosen to maximize SSIM of resulting HR image). Both, the LR image and the reconstruction of the zero-filled k-space are compared as inputs to the neural network. For the qualitative evaluation, saturated low-resolution CEST images are provided to the network and compared with the aforementioned methods.In total, 15 participants gave informed consent and were measured under the approval of the local ethics committee. Images were acquired using a 7T MR Siemens Magnetom Terra (Siemens Healthcare, Erlangen, Germany) with a dedicated 1TX/28RX knee coil (Quality Electrodynamics, Mayfield Village, OH). All images were acquired with a slab selective 3D GRE CEST sequence with elliptical scanning [5,6]. Scanning parameters for the unsaturated knee scans used for training were: TR 13ms, TE 1.81ms, 6.43ms, and 11.05ms, FOV 154mm×154mm, base resolution of 192×192 and 40 slices with a slice thickness of 2.5mm. For qualitative evaluation, CEST knee images with comparable acquisition but halved resolution and a pulsed saturation train of 2.2s length, B1,rms=2.37μT and duty cycle of 99% were acquired. The head measurement was acquired with measurement parameters as described in [7] for one saturation level of B1,rms=0.7μT. For the CEST contrasts, a B0 correction based on the CEST spectra was performed and an offset wise asymmetry contrast (MTRasym) was calculated.
Knee scans of 10 patients were used for the training with 3 TEs each, resulting in 30 volumes, that were z-score normalized and, for the training phase, randomly flipped along all three axes. The mean-squared-error was used as loss function for the optimization with Adam (learning rate 1e-4). The neural network builds upon the ResNet blocks described in [8] with 16 residual blocks with equal feature dimensions and one up-sampling block doubling the feature dimension extend. For comparison to the neural network, trilinear interpolation and k-space zero-filling are used.
Results
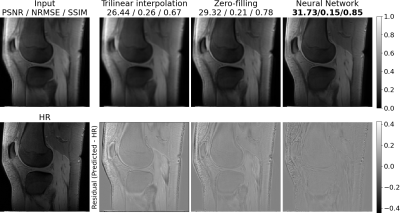
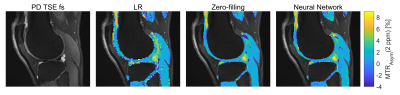
Table 1 shows the quantitative comparison of trilinear interpolation, k-space zero-filling, and the neural networks on unsaturated MR images. The neural network with LR input performs slightly better than the trilinear interpolation, however, does not outperform the k-space zero-filling. The neural network with k-space zero-filling input outperforms all other methods. These quantitative results can be confirmed on a qualitative level when looking at the non-saturated image in Figure 1. While the trilinear interpolation and the zero-filled image have stronger errors at the regions of the joints, errors of the neural network are mostly only present in the region with high-frequency structures such as the subcutaneous fat. A qualitative comparison of k-space zero-filling and the prediction of the neural network is made using the CEST contrast calculated from the predicted HR offsets in Figure 2. Both, the zero-filled and the predicted image present a substantially increased apparent resolution compared to the LR image without altering the mean CEST contrast.On generalization
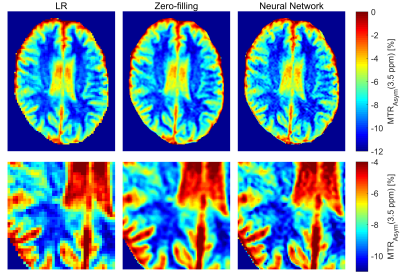
Figure 3 provides an insight into the generalization of the proposed method through the evaluation of the network trained using knee scans applied to head scans. The prediction of the neural network results in a CEST contrast very similar to the zero-filling-based contrast, whereas both substantially improve the apparent resolution.
Discussion
The presented work showed promising results for the estimation of high-resolution CEST MR images. We were able to demonstrate the generalizability of the network by applying it successfully to out-of-distribution brain MR scans with high similarity to the zero-filled solution. Lastly, we could show, that using prior knowledge in the form of the k-space zero-filling as input is beneficial to the problem with greatly enhanced performance in contrast to the LR input [9].Our approach has limitations. First, it can be shown that the width of the point-spread-function broadens with an increased number of acquired k-space lines for the used elliptical readout [5], which might reduce the effective resolution gain of our network. Second, no quantitative evaluation of the CEST contrast was made. In the future, we will acquire HR reference scans using a segmented k-space scan.
Acknowledgements
This work was supported by the emerging field initiative (project 4 Med 05“MIRACLE”) of the Universität Erlangen-Nürnberg and MASCARA - Molecular Assessment of Signatures Characterizing the Remission of Arthritis Grant 01EC1903A. We would like to thank the d.hip for computational support.
Lukas Folle and Katharina Tkotz contributed equally to this work.
References
[1] B. Wu et al. “An overview of CEST MRI for non-MR physicists”. eng. In: EJNMMI physics 3.1 (Dec. 2016). PMC4999387[pmcid], pp. 19–19. issn:2197-7364. doi:10.1186/s40658-016-0155-2. url:https://doi.org/10.1186/s40658-016-0155-2.
[2] H. Greenspan et al. “MRI inter-slice reconstruction using super-resolution”. In: Magnetic Resonance Imaging 20.5 (2002), pp. 437–446. issn: 0730-725X. doi:https://doi.org/10.1016/S0730-725X(02)00511-8. url:https://www.sciencedirect.com/science/article/pii/S0730725X02005118.
[3] Akshay S. Chaudhari et al. “Super-resolution musculoskeletal MRI using deep learning”. In: Magnetic Resonance in Medicine 80.5 (2018), pp. 2139–2154. doi:https://doi.org/10.1002/mrm.27178. eprint:https ://onlinelibrary.wiley.com/doi/pdf/10.1002/mrm.27178. url:https://onlinelibrary.wiley.com/doi/abs/10.1002/mrm.27178.
[4] F. Rousseau et al. “On Super-Resolution for Fetal Brain MRI”. In: Medical Image Computing and Computer-Assisted Intervention – MICCAI 2010. Springer Berlin Heidelberg, 2010, pp. 355–362. doi:10.1007/978-3-642-15745-5_44. url:https://doi.org/10.1007/978-3-642-15745-5_44.
[5] Moritz Zaiss, Philipp Ehses, and Klaus Scheffler. “Snapshot-CEST: Optimizing spiral-centric-reordered gradient echo acquisition for fast and robust 3D CEST MRI at 9.4 T”. In: NMR in Biomedicine31.4 (2018). e3879 NBM-17-0188.R2, e3879. doi:https://doi.org/10.1002/nbm.3879. eprint:https://analyticalsciencejournals.onlinelibrary.wiley.com/doi/pdf/10.1002/nbm.3879. url:https://analyticalsciencejournals.onlinelibrary.wiley.com/doi/abs/10.1002/nbm.3879.
[6] Andrzej Liebert et al. “Multiple interleaved mode saturation (MIMOSA) for B1+ inhomogeneity mitigation in chemical exchange saturation transfer”. In: 82.2 (Apr. 2019), pp. 693–705. doi:10.1002/mrm.27762. url:https://doi.org/10.1002/mrm.27762.
[7] Alexander German et al. “Brain tissues have single-voxel signatures in multi-spectral MRI”. In: NeuroImage234 (2021), p. 117986. issn: 1053-8119. doi:https://doi.org/10.1016/j.neuroimage.2021.117986. url:https://www.sciencedirect.com/science/article/pii/S1053811921002639.
[8] Kaiming He et al. “Deep Residual Learning for Image Recognition”. In: 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 2016, pp. 770–778. doi:10.1109/CVPR.2016.90.
[9] Andreas K. Maier et al. “Learning with known operators reduces maximum error bounds”. In: Nature Machine Intelligence 1.8 (Aug. 2019), pp. 373–380. issn:2522-5839. doi:10.1038/s42256-019-0077-5. url:https://doi.org/10.1038/s42256-019-0077-5.
Figures