2077
Optimization of Pulsed Chemical Exchange Saturation Transfer MRI by Optimal Control
Clemens Stilianu1, Christina Graf1, Clemens Diwoky2, Martin Soellradl1, Armin Rund3, Moritz Zaiss4, and Rudolf Stollberger1
1Medical Engineering, TU Graz, Graz, Austria, 2647 Institut für Molekulare Biowissenschaften, University of Graz, Graz, Austria, 3Institute for Mathematics and Scientific Computing, University of Graz, Graz, Austria, 4Department High-field Magnetic Resonance, Max Planck Institute Tübingen, Tübingen, Germany
1Medical Engineering, TU Graz, Graz, Austria, 2647 Institut für Molekulare Biowissenschaften, University of Graz, Graz, Austria, 3Institute for Mathematics and Scientific Computing, University of Graz, Graz, Austria, 4Department High-field Magnetic Resonance, Max Planck Institute Tübingen, Tübingen, Germany
Synopsis
We optimized CEST saturation pulse train using an optimal control framework and validated the simulation results on a preclinical scanner that allowed also Gold Standard continuous wave saturation. The optimized pulses almost reached the same saturation as the continuous wave pulse while addressing the allowed duty cycle and SAR limitations of clinical scanners. In measurements, the optimized pulses outperform state-of-the-art Gaussian pulses by over $$$47\%$$$.
Introduction
Chemical Exchange Saturation Transfer (CEST)-MRI can efficiently detect various metabolites in the human body, overcoming the concentration limitations of conventional MRS$$$^1$$$. In NMR, this is typically realized by applying a long, Continuous Wave (CW) saturation RF pulse of several seconds at certain off-resonant frequencies. Those pulses are not always executable due to hardware limitations and SAR constraints, especially on clinical scanners that require pulsed RF excitation. In contrast to CW saturation, pulsed saturation typically provides much less CEST-effect. Currently, CEST experiments use Duty-Cycled (DC) Gaussian or Sinc-shaped pulse trains. Optimization of the Gaussian pulse shapes has been shown to have impact on the contrast of CEST measurements$$$^2$$$. In this work, we design CEST pulses by Optimal Control (OC) and compared it with CW and Gaussian pulses in simulations and in a creatine phantom. We show that OC pulses outperform Gaussian pulses and challenge CW pulses on a preclinical $$$7T$$$ scanner.Theory and Methods
The basis of this work are two pool Bloch-McConnell equations, with one pool for the on-resonant free water and one pool for the off-resonant solute. The cost function for the optimization is given as:\begin{align*} &\underset{B_1}{\min} \ J(B_1,M_z,\tilde{M}_z)=\frac{\alpha}{2}\int\limits_{0}^{T}B_1^{2} dt-\beta |M_z(z_1)-\tilde{M}_{z}(z_1)|-\gamma \int\limits_{\Omega}\tilde{M}_z(z_1) dz.\end{align*} The magnetization of the water pool without chemical exchange is $$$\tilde{M}$$$ and the magnetization of the water pool with exchange is $$$M$$$. $$$B_1$$$ is the complex, free-form RF pulse. The first integral corresponds to the total transmitted energy, the second term maximizes the difference between $$$M_z(z_1)$$$ and $$$\tilde{M}_z(z_1)$$$, which corresponds to the amplitude of the CEST peak. The third term maximizes the spectrum's area$$$^2$$$. $$$\Omega$$$ describes the points in the spectrum, where $$$z_1$$$ is the frequency of the solute pool. The optimization is regularized by $$$\alpha$$$ and penalized by $$$\beta$$$ and $$$\gamma$$$. In the simulation, the relaxation times of the water pool are assumed to be $$$T_{1w}=1.084$$$ $$$s$$$ and $$$T_{2w}=0.069$$$ $$$s$$$. For the solute pool we assumed $$$T_{1s}=1.000$$$ $$$s$$$ and $$$T_{2s}=0.160$$$ $$$s$$$. The chemical exchange rate between creatine and water is assumed to be $$$k_{sw}=100$$$ $$$Hz$$$. During optimization, the DC is fixed to $$$90\%$$$ with an on time of $$$t_p=100$$$ $$$ms$$$ and subsequent off times of $$$t_d=12.5$$$ $$$ms$$$. A DC of $$$90\%$$$ is chosen to ensure maximum CEST-effect while still being applicable to clinical scanners$$$^3$$$. To compare the performance, the simulation is also conducted for a CW pulse with a DC of $$$100\%$$$ and a cosine-windowed Gaussian function$$$^4$$$ with the same $$$t_p$$$ and $$$t_d$$$ as the OC pulse. The $$$B_1$$$ amplitudes of the OC pulse and the Gaussian pulse are scaled to the CW equivalent RF power$$$^5$$$, i.e. all have the same total energy. The OC pulse is optimized via hybrid semi-smooth quasi-Newton method$$$^7$$$ which includes the hardware constraints of a clinical scanner. The Bloch-McConnell equations and their corresponding adjoint equations are solved numerically using a symmetric operator splitting algorithm$$$^8$$$. To validate the simulation, RF pulses are implemented on a $$$7T$$$ preclinical scanner (Bruker BioSpec 70/20 USR) which allows implementing CW pulses. The experiments are conducted on a $$$87$$$ $$$mM$$$ creatine monohydrate phantom in a $$$15$$$ $$$ml$$$ tube. The relaxation times are reduced with Manganese(2)chloride to quasi in-vivo conditions. The pH-value was fixed to $$$7.4$$$ with a phosphate buffer. Creatine has a CEST peak at an off-resonance frequency of $$$\Delta\omega=1.9$$$ $$$ppm$$$, therefore the z-spectrum was measured from $$$1$$$ to $$$3$$$ $$$ppm$$$ and from $$$-1$$$ to $$$-3ppm$$$ with increments of $$$0.05$$$ $$$ppm$$$, the CEST-effect is evaluated with MTR asymmetry. In the simulation and in the measurements, the $$$B_1$$$-RMS is set to $$$0.8$$$ $$$\mu T$$$ and the saturation time to $$$1$$$ $$$s$$$. The images were acquired with a RARE-sequence with a TR of $$$10$$$ $$$s$$$.Results and Discussion
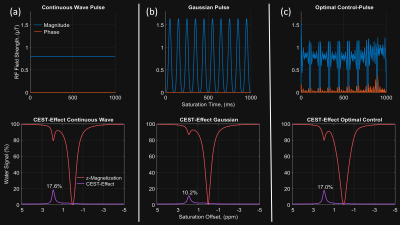
Figure 1 shows the different pulses with the simulated CEST-effect and the corresponding spectrum. It shows a similar CEST-effect for the proposed pulse is $$$17\%$$$ (Figure 1c), which is close to the optimum of $$$17.6\%$$$ by the CW pulse (Figure 1a) and by $$$67.43\%$$$ larger than for the Gaussian pulse (Figure 1b). Figure 2 compares the simulated with the measured CEST-effect. In the simulation, the CEST peak maximum of the OC pulse reaches the CEST peak maximum of the CW within approximately $$$3.4\%$$$ and beats the maximum of the Gaussian pulse by about $$$67.4\%$$$. This is in agreement with the experimental data, where the maximum CEST peak of the OC pulse reached the maximum of the CW within $$$2.8\%$$$ and the beat the maximum of the Gaussian pulse by over $$$47.1\%$$$. Simulation suggests a narrower peak for the CW pulse than for the OC pulse, but in measurement, the peak quality of the OC pulse appears to be comparable to that of the CW pulse. The OC pulses showed significant higher CEST contrast than Gaussian pulses for the creatine model and tend to reach the theoretical maximum of the CEST-effect for the same energy (see Figure 3).Conclusion
We showed that with the proposed OC framework we were able to outperform state-of-the-art Gaussian pulses by $$$47.1\%$$$ on $$$7T$$$ preclinical scanner. The optimized pulses show the potential to significantly increase the contrast for in vivo clinical CEST imaging.Acknowledgements
No acknowledgement found.References
1. S. A. Smith, J. A. D. Farrell, C. K. Jones, D. S. Reich, P. A. Calabresi, and P. C. M. Van Zijl, “Pulsed magnetization transfer imaging with body coil transmission at 3 Tesla: Feasibility and application,” Magn. Reson. Med., vol. 56, no. 4, pp. 866–875, Oct. 2006, doi: 10.1002/mrm.21035.2. E. S. Yoshimaru, E. A. Randtke, M. D. Pagel, and J. Cárdenas-Rodríguez, “Design and optimization of pulsed Chemical Exchange Saturation Transfer MRI using a multiobjective genetic algorithm,” J. Magn. Reson., vol. 263, pp. 184–192, Feb. 2016, doi: 10.1016/j.jmr.2015.11.006.3. P. Z. Sun, J. Lu, Y. Wu, G. Xiao, and R. Wu, “Evaluation of the dependence of CEST-EPI measurement on repetition time, RF irradiation duty cycle and imaging flip angle for enhanced pH sensitivity,” Phys. Med. Biol., vol. 58, no. 17, Sep. 2013, doi: 10.1088/0031-9155/58/17/N229.4. K. Herz et al., “Pulseq-CEST: Towards multi-site multi-vendor compatibility and reproducibility of CEST experiments using an open-source sequence standard,” Magn. Reson. Med., vol. 00, pp. 1–14, 2021, doi: 10.1002/mrm.28825.5. Sun, Phillip Zhe, et al. "Investigation of optimizing and translating pH‐sensitive pulsed‐chemical exchange saturation transfer (CEST) imaging to a 3T clinical scanner." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 60.4 (2008): 834-841.6. M. Zaiss, B. Schmitt, and P. Bachert, “Quantitative separation of CEST-effect from magnetization transfer and spillover effects by Lorentzian-line-fit analysis of zspectra,” J. Magn. Reson., vol. 211, no. 2, pp. 149–155, Aug. 2011, doi: 10.1016/j.jmr.2011.05.001.7. A. Rund, C. S. Aigner, K. Kunisch, and R. Stollberger, “Magnetic Resonance RF Pulse Design by Optimal Control with Physical Constraints,” IEEE Trans. Med. Imaging, vol. 37, no. 2, pp. 461–472, Feb. 2018, doi: 10.1109/TMI.2017.2758391.8. C. Graf, A. Rund, C. S. Aigner, and R. Stollberger, “Accuracy and Performance Analysis for Bloch and Bloch-McConnell Simulation Methods,” J. Magn. Reson., p. 107011, May 2021, doi: 10.1016/j.jmr.2021.107011.Figures
Comparison of the simulation and the measurement data for the optimized , CW and Gaussian pulse. The pulses ware measured on a 7T preclinical Bruker system for a $$$87$$$ $$$ml$$$ creatine phantom. The optimized pulse beats the Gaussian pulse in simulation and in measurement and provides a comparable CEST peak maximum as the CW pulse.
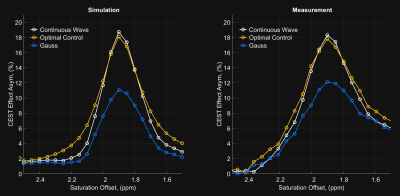
Comparison of the simulation and the measurement data for the optimized , CW and Gaussian pulse. The pulses ware measured on a 7T preclinical Bruker system for a $$$87$$$ $$$ml$$$ creatine phantom. The optimized pulse beats the Gaussian pulse in simulation and in measurement and provides a comparable CEST peak maximum as the CW pulse.
Comparison of the pulse features of Continuous Wave (CW) pulse, Gaussian pulse train, and the optimized pulse train (OC). To meet the hardware constraints of clinical scanners, the duty cycle is set to 90 $$$\%$$$ for the Gaussian and the OC pulse with an on-time of $$$100$$$ $$$ms$$$ and pauses of $$$12.5$$$ $$$ms$$$. For comparing the pulses, the $$$B_1-RMS$$$ and therefore, the energy of the pulses, were set to the same value.
DOI: https://doi.org/10.58530/2022/2077