2071

Data-driven B1 non-uniformity correction in ultra-high-field small-animal macromolecular proton fraction and R1 mapping
Vasily L. Yarnykh1, Alena A. Kisel1, Andrey E. Akulov2, and Alexander Drobyshevsky3
1Radiology, University of Washington, Seattle, WA, United States, 2Institute of Cytology and Genetics, Siberian Branch of the Russian Academy of Sciences, Novosibirsk, Russian Federation, 3NorthShore University HealthSystem, Evanston, IL, United States

Synopsis

The data-driven surrogate B1 field correction algorithm was recently developed to eliminate B1-related spatial errors in the macromolecular proton fraction (MPF) and R1 maps obtained using the fast single-point method. The algorithm obviates the need for acquisition of actual B1 field maps, thus extending the routine use of fast MPF mapping. Initially, the surrogate B1 correction was applied to the human brain imaging at 3T. In this study, the method has been adopted and validated for small-animal imaging utilizing dedicated ultra-high-field MRI scanners. Particularly, we report guidelines on using surrogate B1 field correction in 9.4T and 11.7T magnetic fields.

Introduction

Over past years, fast macromolecular proton fraction (MPF) mapping1,2 has gained a substantial interest as a quantitative myelin imaging approach for both clinical and preclinical studies. One limitation of this technique is the need in supplementary B1 mapping to correct B1-related errors3. To overcome this limitation, the data-driven surrogate B1 field mapping method4 was recently introduced. This method exploits the distinctions in B1 dependences of MPF and R1=1/T1 to reconstruct a B1 map (termed below a surrogate B1 map) from uncorrected MPF and R1 maps4. In the initial proof-of-principle study4, the surrogate B1 correction technique was applied to the human brain imaging at 3T. The goal of this study was to adopt and validate surrogate B1 correction for small-animal imaging utilizing dedicated ultra-high-field MRI systems.

Theory and Study Design

The data driven reconstruction of a surrogate B1 field map4 is based on the calculation of a field scaling factor (cs) from R1 measured by the variable flip-angle method and MPF fitted using the single-point algorithm1,2 under assumption of an approximately linear relationship between R1 and MPF:
cs2 = [r0(1-fm)+rfPfm]/[R1m(1-fm)-rf(1-P)fm],
where R1m and fm are the R1 and MPF measured without B1 correction; r0 and rf are the coefficients of linear regression R1=r0+rff/(1-f) for the actual R1 and MPF values; and P=R/(R+R1m+Wtmt/TR), where W is the saturation rate of the macromolecular proton pool (calculated from the superLorentzian line shape and parameters of the saturation pulse1), R is the cross-relaxation rate constant (fixed parameter in the single-point algorithm1), and tmt is the duration of the saturation pulse. The algorithm constants r0 and rf need to be specified for a particular magnetic field strength. Accordingly, we measured their mean values in 9.4T and 11.7T fields based on actual B1 correction and then used them uniformly to test accuracy of surrogate B1 correction.

Methods

MRI acquisition: Two groups of C57BL/6 mice (N=7 each) were scanned in vivo on two Bruker Biospec small-animal MRI units with magnetic field strengths of 9.4T and 11.7T. The fast MPF mapping protocols were identical and included the three 3D spoiled gradient echo sequences according to the synthetic-reference method2:
1) MT-weighted: TR=22 ms, flip angle (FA) = 9°, 4 signal averages, off-resonance saturation by the Gaussian pulse with offset frequency 4.5 kHz, effective FA=900°, and tmt=10 ms, scan time 10.5 min;
2) T1-weighted: TR=16 ms, FA=16°, 4 signal averages, scan time 8 min;
3) Proton-density-weighted: TR=16 ms, FA=3°, 4 signal averages, scan time 8 min.
All sequences were applied in the coronal plane with TE=2.5 ms, 3D FOV 20×20×24 mm, and resolution 100×100×500 μm3. B1 field maps were obtained using the actual flip-angle imaging (AFI) method5,6 with TR1/TR2=13/65 ms, TE=3.7 ms, FA=60°, resolution 200×200×500 μm3, and scan time 5 min.
Image processing: Brain masks were manually created using ImageJ software7. Other reconstruction steps were carried out using custom-written C++ language software tools available online8. R1 and MPF maps were first reconstructed by the single-point synthetic-reference algorithm2 using AFI B1 maps for B1 non-uniformity correction. Voxel-based linear regressions between R1 and MPF/(1-MPF) was used to determine the algorithm constants r0 and rf for each animal. Then, based on the mean values of the constants for the entire dataset, B1s maps were computed from uncorrected R1 and MPF maps. Finally, the resulting B1s maps were applied to correct R1 and MPF maps.
Statistics: Algorithm constants r0 and rf were compared between the two field strengths using the independent-samples t-test. For each field strength, mean whole-brain MPF and R1 values were compared between the three reconstruction options (actual B1, surrogate B1, and no correction) using paired t-tests and Bland-Altman plots.

Results

Determination of the algorithm constants: The mean ±SD values of the constants were: r0=0.29±0.02, rf=2.02±0.12 for 9.4T and r0=0.29±0.01, rf=2.09±0.09 for 11.7T. No significant differences between magnetic fields was found for both r0 (P=0.99) and rf (P=0.24). Further processing was carried out with the rounded values r0=0.3 and rf=2.0.
Accuracy of surrogate B1 correction: Surrogate B1 field maps closely reproduced actual B1 field distribution (Fig. 1). R1 and MPF maps reconstructed without B1 correction showed apparent propagation of spatially dependent B1-related errors (Fig. 1) and significant bias in the whole-brain parameter measurements (P<0.001) as indicated by the Bland-Altman plots (Fig. 2). Correction of R1 and MPF maps using surrogate B1 field reduced the biases to a non-significant level, as seen in Fig. 2 (P=0.15 at 9.4T and P=0.50 at 11.7T for MPF; P=0.19 at 9.4T and P=0.64 at 11.7T for R1) and markedly improved uniformity of the resulting parametric maps (Fig. 1).

Conclusions

The surrogate B1 correction method improves time-efficiency of MPF and R1 mapping in ultra-high magnetic fields by obviating the need in actual B1 mapping. The algorithm constant r0 appears independent of magnetic field strength based on comparison with previous measurements at 3T and can be uniformly used with the value r0=0.3. The constant rf differs from its 3T value (rf=4.5)4 but shows no significant distinctions between 9.4 and 11.7T fields. For these field strengths, the value rf=2 is recommended.

Acknowledgements

Grant support: National Institutes of Health grants R24NS104098, R21NS109727, R01NS119251, and R21NS109838. Russian Science Foundation grants #14-45-00040 and #19-75-20142.

References

  1. Yarnykh VL. Fast macromolecular proton fraction mapping from a single off-resonance magnetization transfer measurement. Magn Reson Med 2012;68(1):166-178.
  2. Yarnykh VL. Time-efficient, high-resolution, whole brain three-dimensional macromolecular proton fraction mapping. Magn Reson Med 2016;75(5):2100-2106.
  3. Yarnykh VL, Kisel AA, Khodanovich MY. Scan-Rescan Repeatability and Impact of B(0) and B(1) Field Nonuniformity Corrections in Single-Point Whole-Brain Macromolecular Proton Fraction Mapping. J Magn Reson Imaging 2020;51(6):1789-1798.
  4. Yarnykh VL. Data-driven Retrospective Correction of B1 Field Inhomogeneity in Fast Macromolecular Proton Fraction and R1 Mapping. IEEE Trans Med Imaging 2021 Jun 10; doi: 10.1109/TMI.2021.3088258.
  5. Yarnykh VL. Actual flip-angle imaging in the pulsed steady state: a method for rapid three-dimensional mapping of the transmitted radiofrequency field. Magn Reson Med 2007;57(1):192-200.
  6. Yarnykh VL. Optimal radiofrequency and gradient spoiling for improved accuracy of T1 and B1 measurements using fast steady-state techniques. Magn Reson Med 2010;63(6):1610-1626.
  7. ImageJ: Image Processing and Analysis in Java. https://imagej.nih.gov/ij/.
  8. Macromolecular Proton Fraction (MPF): Quantitative Myelin Mapping Technique for Neuroscience. https://www.macromolecularmri.org/.

Figures

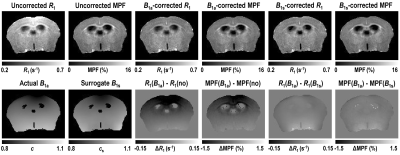
Fig. 1. Application of the surrogate B1 field correction algorithm to the murine brain R1 and MPF maps obtained at 11.7 T. Top row: uncorrected, corrected with actual B1 field, and corrected with surrogate B1 field R1 and MPF maps. Bottom row: actual and surrogate B1 maps and subtraction images between corrected with actual B1 and either uncorrected or corrected with surrogate B1 R1 and MPF maps. Surrogate B1 correction effectively eliminates large field-dependent deviations from R1 and MPF maps with minor residual variations.

Fig. 2. Bland-Altman plots comparing whole-brain MPF (a, b) and R1 (c, d) values measured with actual B1 (B1a) correction to those measured without correction (a, c) and with surrogate B1 (B1s) correction (b, d). The plots are presented for the pooled dataset including the maps obtained on both 9.4T (triangles) and 11.7T (circles) scanners. Solid and dashed lines indicate the mean differences and limits of agreement, respectively.


Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)
2071
DOI: https://doi.org/10.58530/2022/2071