2068
Quantifying myelin water exchange using optimized bSSFP sequences1Electrical Engineering and Computer Science, University of Michigan, Ann Arbor, MI, United States, 2fMRI Lab, University of Michigan, Ann Arbor, MI, United States, 3Radiology, University of Michigan, Ann Arbor, MI, United States
Synopsis
Mapping myelin water exchange rates could potentially be useful in helping us understand and characterize different diseases in the brain. It is a challenging quantitative parameter mapping problem to estimate multi-compartment exchange. This work focuses on scan design, with an aim of estimating exchange maps with good precision. In particular, a set of balanced steady-state free precession (bSSFP) sequences are optimized to estimate exchange rates in white matter (WM), for a two-pool model. Quantitative exchange maps are shown for a simulated phantom, using this optimized scan design.
Introduction
Exchange dynamics between water compartments in living tissue has been suggested as a biomarker for several clinical applications$$$^{1}$$$. Prior work has shown that it may be possible to map multi-compartment exchange rates using Magnetic Resonance Fingerprinting based approaches$$$^{2}$$$. In this work, we aim to improve the precision of exchange estimates by optimizing the scan parameters of bSSFP sequences. Using the optimized scan design, exchange maps are estimated for a simulated phantom, and are shown in the results.Methods
A two-pool model was used, with a fast-relaxing myelin water compartment and a slow-relaxing non-myelin water compartment, each with its own time constants and volume fraction. Exchange dynamics were modeled through the mean residence time ($$$\tau_{\mathrm{fs}}$$$), which is the inverse of the exchange rate between the two compartments. Additionally, an (unknown) orientation-dependent frequency shift that is specific to the myelin water pool is also included$$$^{3}$$$. The signal was modeled using the Bloch-McConnell equations$$$^{4}$$$ .The acquisition parameters were optimized for a set of 40 bSSFP images by minimizing the Cramer-Rao Bound (CRB) on the variance of unbiased exchange estimates; TR/TE were fixed at 20ms/4ms,and the flip angles ($$$\alpha$$$) and RF phase cycling factors ($$$\phi$$$) of the bSSFP scans were optimized. The flip angles were constrained to lie between $$$10^\circ$$$ and $$$40^\circ$$$. For the scan design optimization, we focused on estimating the exchange between the two compartments of white matter (WM) tissue, because grey matter (GM) has very low myelin content.The scan design is optimized over a range of bulk off-resonance values (-25Hz to 25Hz), and myelin-specific frequency shifts (0-10Hz). Mean residence times in the range of 50ms-250ms are considered during scan design. We assume B0 and B1+ maps to be known parameters. In practice, these can be estimated from separate spoiled gradient-recalled echo (SPGR) and Bloch-Siegert$$$^{5}$$$ acquisitions respectively. After scan design, myelin water exchange is estimated from the optimized bSSFP images using a kernel-based estimation method called PERK$$$^{6}$$$. Though the scan design process focused on WM, PERK is trained over a wider range of tissue parameter distributions$$$^{7}$$$ so as to make it more generalizable to other tissue types.
Results
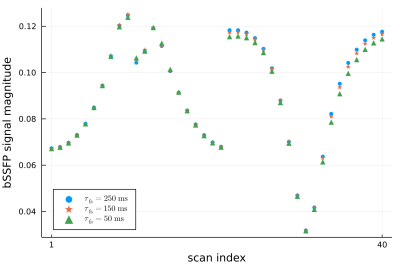
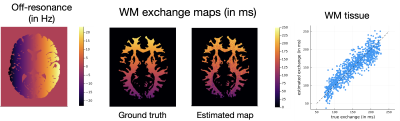
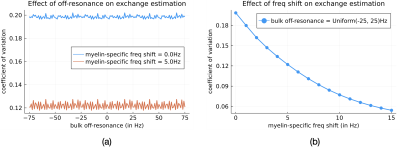
The optimized bSSFP scan design (shown in Fig. 1) has a predicted coefficient of variation of about 13% for estimating exchange between the two pools in WM, at an average image SNR of about 50dB. Simulations were performed for a typical WM voxel using this optimized scan design, under three different exchange regimes (mean residence times of 50ms, 150ms and 250ms). Fig. 2 shows the resulting signal magnitudes from this tissue with the optimized acquisition parameters. Fig. 3 shows simulations using a BrainWeb$$$^{8}$$$ phantom with a range of residence times from anterior to posterior. The estimated exchange map has an RMSE of approximately 12.5% in WM. The exchange estimates are unreliable in GM and have been masked out. Fig. 4 shows how exchange estimation is affected by bulk off-resonance and the myelin-specific frequency shift. The predicted coefficient of variation of exchange remains relatively uniform with bulk off-resonance, while it increases as the myelin-specific frequency shift goes towards 0Hz.Discussion
Starting from a randomly initialized scan design, it is intriguing that the optimized bSSFP scan design has a very regular sweep of phase-cycling factors $$$\phi$$$ at both the low and high flip angles (see Fig. 1). This variation in $$$\phi$$$ appears to be quite important for exchange estimation; the predicted coefficient of variation was much worse when $$$\phi$$$ was kept fixed across scans. The mcDESPOT$$$^{9, 10}$$$ approach to myelin water fraction (MWF) estimation also uses a set of bSSFP scans with $$$\phi$$$ fixed to $$$0^\circ$$$ or $$$180^\circ$$$; a future direction could be to design a set of $$$\phi$$$ values to optimize MWF precision. Fig. 2 shows that it is hard to distinguish between exchange regimes on a per-scan basis; however, the predicted coefficient of variation suggests that, between them, the 40 scans could contain enough diversity and information to estimate exchange with good precision.The exchange maps and scatter plot in Fig. 3 show that the WM exchange estimates are close to the ground truth, even in the presence of field inhomogeneities. Fig. 4 suggests that the optimized design is robust to off-resonance, and this property would be interesting to explore further, with in vivo data. A natural extension of this work would be to consider phase information, along with transient data, instead of just magnitude data of bSSFP scans. Because PERK is a dictionary-free estimator, our approach for exchange estimation scales well even when modeling more tissue compartments.
Conclusion
This preliminary study shows that multi-compartment exchange rates could be estimated with good precision using optimized bSSFP acquisitions. We presented WM exchange maps for simulated data using the optimized bSSFP scan design. In additional comparisons (not shown), we found that optimizing the phase factors $$$\phi$$$ for the bSSFP scans greatly improved exchange estimation compared to using a fixed $$$\phi$$$ value. It would be interesting to see if this would be beneficial for estimating other quantitative tissue parameters.Acknowledgements
This work was supported in part by NSF Grants CBET 1553441 and IIS 1838179.References
[1] Kim, S., Quon, H., Loevner, L.A., Rosen, M.A., Dougherty, L., Kilger, A.M., Glickson, J.D. and Poptani, H., 2007. Transcytolemmal water exchange in pharmacokinetic analysis of dynamic contrast‐enhanced MRI data in squamous cell carcinoma of the head and neck. Journal of Magnetic Resonance Imaging, 26(6), pp.1607-1617.
[2] Hamilton, J.I., Deshmane, A., Griswold, M. and Seiberlich, N., 2016, May. MR fingerprinting with chemical exchange (MRF-X) for in vivo multi-compartment relaxation and exchange rate mapping. ISMRM (2016).
[3] Wharton, S. and Bowtell, R., 2012. Fiber orientation-dependent white matter contrast in gradient echo MRI. Proceedings of the National Academy of Sciences, 109(45), pp.18559-18564.
[4] McConnell, H.M., 1958. Reaction rates by nuclear magnetic resonance. The Journal of chemical physics, 28(3), pp.430-431.
[5] Sacolick, L.I., Wiesinger, F., Hancu, I. and Vogel, M.W., 2010. B1 mapping by Bloch‐Siegert shift. Magnetic resonance in medicine, 63(5), pp.1315-1322.
[6] Nataraj, G., Nielsen, J.F., Scott, C. and Fessler, J.A., 2018. Dictionary-free MRI PERK: Parameter estimation via regression with kernels. IEEE transactions on medical imaging, 37(9), pp.2103-2114.
[7] Whitaker, S.T., Nataraj, G., Nielsen, J.F. and Fessler, J.A., 2020. Myelin water fraction estimation using small‐tip fast recovery MRI. Magnetic resonance in medicine, 84(4), pp.1977-1990.
[8] Collins, D.L., Zijdenbos, A.P., Kollokian, V., Sled, J.G., Kabani, N.J., Holmes, C.J. and Evans, A.C., 1998. Design and construction of a realistic digital brain phantom. IEEE transactions on medical imaging, 17(3), pp.463-468.
[9] Deoni, S.C., Rutt, B.K., Arun, T.,
Pierpaoli, C. and Jones, D.K., 2008. Gleaning multicomponent T1 and T2
information from steady‐state imaging data. Magnetic Resonance in Medicine, 60(6), pp.1372-1387.
[10] Deoni, S.C., 2011. Correction of main and transmit magnetic field (B0 and B1) inhomogeneity effects in multicomponent‐driven equilibrium single‐pulse observation of T1 and T2. Magnetic resonance in medicine, 65(4), pp.1021-1035.
Figures