2056
Virtual coil concept applied to motion corrected and low rank undersampled reconstructions1King's College London, London, United Kingdom
Synopsis
Partial Fourier strategies leverage the Hermitian symmetric properties of k-space into higher acceleration factors. Motion corrected (MC) reconstructions incorporate generalized motion into the process. Contrast resolved reconstructions, e.g. low rank inversion (LRI), exploit temporal redundancies in highly accelerated acquisitions. Both the MC and LRI reconstructions are usually ill-posed and can benefit from additional sources of encoding. The Virtual Coil Concept (VCC) has been recently introduced, combining Parallel Imaging with Partial Fourier. Here we investigate the combination of VCC with MC and VCC with LRI to enable further acceleration of both approaches.
INTRODUCTION:
Motion corrected (MC) reconstructions1 allow for retrospective correction of any motion that may occur during acquisition. These reconstructions are often ill-posed, even for a “fully-sampled” acquisition; moreover, they are often combined with accelerated acquisitions for fast, motion corrected scans. Low rank (LR) constrained methods2,3,4 have been proposed for dynamic contrast reconstructions, leveraging temporal redundancies in the data. As scan time is spent encoding different contrasts, the acquired data is often spatially undersampled. Thus, both MC and LR methods are almost always ill-posed and would benefit from additional encoding.The Hermitian symmetry of the Fourier transform of a real object has long been exploited as a source of additional encoding for sub-Nyquist acquisitions. Since the image in MR is rarely purely real, the underlying phase information must be estimated (often from a low resolution, fully sampled region of the data itself) and incorporated into the reconstruction. For Cartesian Partial Fourier sampling, a direct solution is available.5 Several approaches have also provided general frameworks to combine Parallel Imaging and Partial Fourier, including PFPP6, VCC7 and LORAKS.8 Here, we combine the Virtual Coil Concept (VCC) formulism with two different undersampled reconstructions: i) Motion Corrected reconstructions (MC)1 and ii) Low Rank Inversion (LRI).4 The first one can be used to correct for arbitrary motion during the acquisition; the second is useful to resolve dynamic contrast imaging (as required, for example, in MR Fingerprinting9). We hypothesize that combining either of these reconstructions with VCC may improve reconstruction performance in highly undersampled acquisitions.
METHODS:
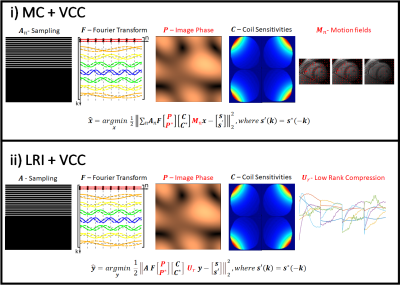
The VCC formulism considers an additional set of synthesized k-space data (and conjugate coil sensitivities) that satisfy the Hermitian symmetry of k-space, $$$S(k) = S^*(-k)$$$ . According to VCC, the Parallel Imaging, Partial Fourier reconstruction may be considered as: $$\hat{x} = \mathit{argmin}_{x} \left \| A F \begin{bmatrix}P\\ P^*\end{bmatrix} \begin{bmatrix}C\\ C^*\end{bmatrix} x - \begin{bmatrix}s\\ s'\end{bmatrix} \right \| _2 ^2$$, where $$$A$$$ is the sampling trajectory, $$$ F $$$ is the Fourier transform, $$$ P $$$is the image phase, $$$ C $$$ are coil sensitivities, $$$ x $$$ is the image, $$$ s $$$ is the acquired k-space and $$$ s'(k) = s^*(-k) $$$ is the synthesized Hermitian k-space data. We will consider the combination of VCC with two other types of undersampled reconstruction: i) Generalized non-rigid Motion Correction (MC) and ii) Low Rank Inversion (LRI).Motion Corrected (MC) reconstructions incorporate generalized motion fields into the process, allowing for correction of any type of motion. MC is obtained by solving: $$ \hat{x} = \mathit{argmin}_{x} \left \| \sum_n A_n F C M_n x - s \right \| _2 ^2 $$, where $$$ A_n $$$ is the sampling for each motion state and $$$ M_n $$$ are the motion fields for each motion state. Incorporating VCC into MC leads to: $$ \hat{x} = \mathit{argmin}_{x} \left \| \sum_n A_n F \begin{bmatrix}P\\ P^*\end{bmatrix} \begin{bmatrix}C\\ C^*\end{bmatrix} M_n x - \begin{bmatrix}s\\ s'\end{bmatrix} \right \| _2 ^2 $$ (Fig. 1i).
Low Rank Inversion (LRI) is a formulism that projects the reconstruction of a dynamic contrast series into a low rank subspace, exploiting the temporally redundant information. The LRI problem can be stated as: $$ \hat{y} = \mathit{argmin}_{y} \left \| A F C U_r y - s \right \|_2^2 $$, where $$$ U_r $$$ are the left singular vectors following a singular value decomposition of the dynamic information (coming from e.g. Bloch simulations or the data itself) and $$$ y $$$ is the set of dynamic images projected into this basis (known as singular images). Combining VCC and LRI results in: $$ \hat{y} = \mathit{argmin}_{y} \left \| A F \begin{bmatrix}P\\ P^*\end{bmatrix} \begin{bmatrix}C\\ C^*\end{bmatrix} U_r y - \begin{bmatrix}s\\ s'\end{bmatrix} \right \| _2 ^2 $$ (Fig.1 ii).
EXPERIMENTS:
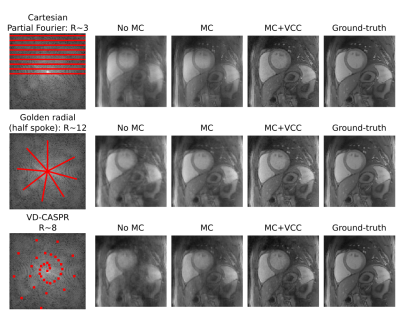
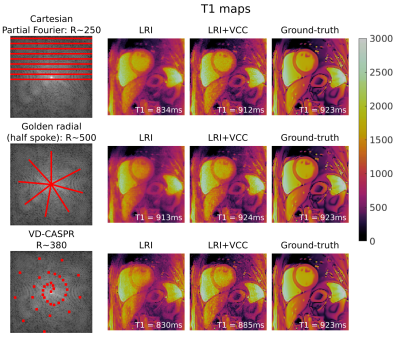
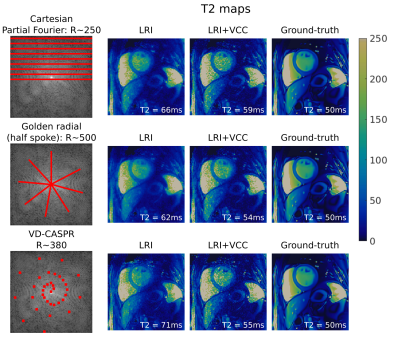
Simulations based on a realistic numerical phantom were performed to investigate the feasibility of two reconstructions: i) MC+VCC and ii) LRI+VCC. In the first case, an acquisition was simulated considering 12 different motion states with respiratory and cardiac motion, including coil sensitivities and white gaussian noise. In the second case, a cardiac MR Fingerprinting sequence for T1/T2 mapping was simulated (as described in10), also including coil sensitivities and white gaussian noise. Following LRI(+VCC), parametric maps were obtained via standard template matching. In both cases, three sampling patterns (with varying degrees of acceleration) were considered: standard Cartesian Partial Fourier, golden radial (half-spoke) and variable density Cartesian with spiral-like order (VD-CASPR11).RESULTS:
Simulated motion corrupted data reconstructed with no motion correction (iterative SENSE), motion correction (MC) and motion correction plus virtual coils (MC+VCC) are shown in Fig.2. Different sampling patterns present different motion artefacts, however all of them have low frequency blurring artefacts even with MC; in contrast, MC+VCC resolves these residual artefacts, leading to improved contrast and apparent sharpness. Simulated MR Fingerprinting data reconstructed with LRI and LRI+VCC are shown in Fig.3 and Fig.4 for T1 and T2, respectively. Similar low frequency artefacts can be observed in both maps which cause residual blurring and potentially bias the quantitative measurements.CONCLUSION:
The Virtual Coil Concept (VCC) was successfully combined with Motion Corrected (MC) reconstruction and with Low Rank Inversion (LRI) reconstruction to incorporate additional encoding in the forward model, allowing for potentially higher acceleration factors. Continued work will evaluate both MC+VCC and LRI+VCC in in-vivo data.Acknowledgements
This work was supported by EPSRC (EP/P001009, EP/P032311/1, EP/P007619/1) and Wellcome EPSRC Centre for Medical Engineering (NS/ A000049/1).References
1. Batchelor PG, Atkinson D, Irarrazaval P, Hill DL, Hajnal J, Larkman D. Matrix description of general motion correction applied to multishot images. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine. 2005 Nov;54(5):1273-80.
2. McGivney DF, Pierre E, Ma D, et al. SVD compression for magnetic resonance fingerprinting in the time domain. IEEE Trans. Med. Imaging 2014;33:2311–2322 doi: 10.1109/TMI.2014.2337321.
3. Zhao B, Setsompop K, Adalsteinsson E, et al. Improved magnetic resonance fingerprinting reconstruction with low-rank and subspace modeling. Magn. Reson. Med. 2018;79:933–942 doi: 10.1002/mrm.26701.
4. Assländer J, Cloos MA, Knoll F, Sodickson DK, Hennig J, Lattanzi R. Low rank alternating direction method of multipliers reconstruction for MR fingerprinting. Magn. Reson. Med. 2018;79:83–96 doi: 10.1002/mrm.26639
5. Noll DC, Nishimura DG, Macovski A. Homodyne detection in magnetic resonance imaging. IEEE transactions on medical imaging. 1991 Jun;10(2):154-63.
6. Bydder M, Robson MD. Partial Fourier partially parallel imaging. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine. 2005 Jun;53(6):1393-401.
7. Blaimer M, Gutberlet M, Kellman P, Breuer FA, Köstler H, Griswold MA. Virtual coil concept for improved parallel MRI employing conjugate symmetric signals. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine. 2009 Jan;61(1):93-102.
8. Haldar JP. Low-rank modeling of local k-space neighborhoods (LORAKS) for constrained MRI. IEEE transactions on medical imaging. 2013 Dec 5;33(3):668-81.
9. Ma D, Gulani V, Seiberlich N, Liu K, Sunshine JL, Duerk JL, Griswold MA. Magnetic resonance fingerprinting. Nature. 2013 Mar;495(7440):187-92.
10. Cruz G, Qi H, Jaubert O, Kuestner T, Schneider T, Botnar RM, Prieto C. Generalized low‐rank nonrigid motion‐corrected reconstruction for MR fingerprinting. Magnetic Resonance in Medicine. 2021 Oct 2.
11. Prieto C, Doneva M, Usman M, Henningsson M, Greil G, Schaeffter T, Botnar RM. Highly efficient respiratory motion compensated free‐breathing coronary MRA using golden‐step Cartesian acquisition. Journal of Magnetic Resonance Imaging. 2015 Mar;41(3):738-46.
Figures