2005
Assessing Universal Code Compression to Lower Wireless MRI Data Rates1Electrical Engineering, Stanford University, Stanford, CA, United States
Synopsis
For wireless MRI data links employing simple ASK or DPSK binary modulation, there is a need to compress the k-space data to lower data rates and use less spectral bandwidth. We explored Fibonacci and Exp-Golomb universal codes for lossless compression. Our results indicate that compression can reduce rates to 1/3 to 1/4 of the original levels. Actual compression will depend on signal gain, as well as k-space trajectories. These results suggest the development of an MRI codec for future wireless or fiber optic RF coil array data links.
Introduction
In developing wireless technology to support MRI receive arrays, a major challenge is data throughput. Wireless standards such as WiFi 6 or WiGig can now support MRI data rates, but the hardware overhead to deploy on an MRI array is severe. These standards require a supporting non-magnetic, low-power, high-speed embedded linux processor that does not emit RF interference. An alternative approach is to use simple binary modulation, either amplitude shift keying (ASK) or differential phase shift keying (DPSK) of a microwave oscillator. ADC data, with minimal FPGA processing, is streamed directly to the modulator as is the case with optic fiber links. The required spectral bandwidth now scales linearly with data rate (Fig. 1). Since MRI is performed in a shielded environment, a bandwidth in the ultra-wideband (UWB) range of 3-10GHz is available, but signal impairments worsen as spectral bandwidth increases. Here, we assess whether code compression can reduce the data rate, and hence spectral bandwidth needs. Two universal code compression methods, Fibonacci coding and Exp-Golomb coding are employed with apriori MRI data to identify the extent that integer ADC k-space data can be compressed.Code Methods
Universal codes map positive integers onto binary codewords, providing short codes for small numbers but long codewords for large integers. MRI k-space data is very noise-like with few large values only at the center of k-space, making it an ideal candidate for compression. First, integer data x<=0 is remapped to y=-2x (even integers) and positive integers to y= 2x-1 (odd integers). For Fibonacci codes, the Fibonacci sequence F=[1, 2, 3, 5, 8, 13 ... ] is used. One finds the largest Fibonacci number F(m) that subtracts from y+1, and progressively subtracts, coding a 1 or zero depending on whether each smaller F(n) is subtracted. The code is then terminated with an extra1 and bit reversed. For Exp-Golomb, one chooses integer parameter k>=0, and computes w=y+2^k. Count the binary bits N in w, and then prefix this word with N-k-1 zeros. For reference, we also tabulate the total number of significant bits in the dataset, P=1+floor(log2(y)), counting y=0 as 1 bit.Image Analysis Methods
We first constructed a numerical "box" model which forms a SINC(x)SINC(y) k-space dataset that is scaled to fit a nominal 16 bit analog-to-digital converter (ADC). Noise-free images, and image SNRs of 10 and 100 were simulated. In each of these, signal/noise scaling was adjustable, mimicking adjustable gain levels. High gain levels cause the noise floor to occupy more bits while the k-space center approaches the maximum ADC range. The synthesized integer k-space values were then coded and the total code-bits counted, as well as that of the uncoded data, to allow construction of bit histograms. The process was repeated with prior MRI datasets of the brain.Results
The box simulations are shown in Fig. 2. This 256x256 example showed a 23-24% reduction by Fibonacci and Exp-Golomb coding at SNR=100. Of the nominal 2*256^2*16 bits, only 13% were significant. As noise was added and scaling gain increased, noise occupies more and more bits, and lowers compressibility. At SNR=10, results degraded to 34-35% compression, with 21% significant bits. In Fig. 3, a similar scaling process of k-space data and histograms is shown for the brain data. Excessive scaling creates a large low-bit histogram for uncoded and coded data. However one sees that compression to about 22-24% is achievable. When data was scaled 6x, mimicking a gain increase, compression degraded to over 40%. In these results, the k=2 Exp-Golomb parameter tended to be near optimum, but not significantly different than Fibonacci coding. Importantly, Fibonacci Codes are self-synchronizing as "11" only appears at the end the code.Discussion
Even these simple computations identify several intriguing issues. MRI compression can be defeated by over-aggressive gain levels that allows noise to occupy many bits. It is imperative that noise levels be about 10dB above the ADC floor to minimize this, even for low dynamic range data. Typical compression levels of 25-40% were achieved, which implies the effective data rates and spectral bandwidths could drop by a factor of 2.5 to 4. This would simultaneously lead to more robust transmission with fewer impairments, and allow more coil sub-channels in a given total bandwidth. Equally important, the compression of the integer k-space data makes room for error correction, with LDPC codes (low density parity check) preferred. These results derived bit counts assuming a cartesian trajectory, but compression will depend on k-space trajectory. If a radial trajectory were used, k-space peaks would be traversed repeatedly, requiring more bits. 3D encoding, whether generally cartesian or radial, would likely show more profound compression ranges. Much like voice and video, this work points to the need for an MRI Codec, that best exploits the statistical properties of the k-space data for maximum lossless compression.Conclusions
Fibonacci coding and Exp-Golomb coding were explored for compression of k-space MRI data. Typically, a reduction to only 25-40% of the original bit count was achievable. This means that for wireless MRI data transmission (and even fiber optic links), 2.5x to 4x slower data rates could be employed for the same net image throughput. This work begins the research process for an MRI data Codec.Acknowledgements
NIH grants: U01EB029427, R01EB01924105, R01EB012031, U01EB026412, GE HealthcareReferences
1 G Scott, S Vasanawala, F Robb, J Pauly, “BPSK/ASK Wireless Link Assessment for MRI”, Proc 28th ISMRM, p759, Aug 2020.
2 A Chan, F Robb, J Pauly, S Vasanawala, G Scott, “Test Bed for High Speed Serial Wireless MRI Data Studies”, Proc 29th ISMRM, p4274, May 2021
Figures
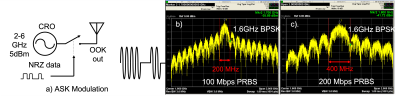
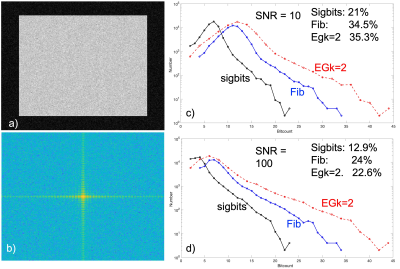
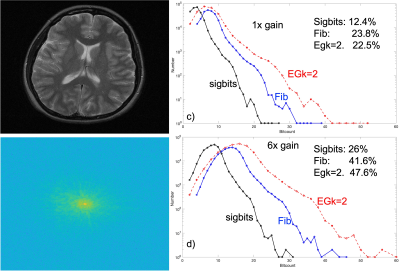
Fig 3: Head MRI compression results. a, b) head image and log kspace representations. c) Histograms at low scaling, and d) 6x higher scaling. Now the noise floor occupies more bits and feasible compression degrades from 23% to over 40%.