1957

Retrospective motion correction with structural priors for clinical MRI protocols 
Gabrio Rizzuti1, Niek Huttinga2, Alessandro Sbrizzi2, and Tristan van Leeuwen3
1Utrecht University, Utrecht, Netherlands, 2Universitair Medisch Centrum Utrecht, Utrecht, Netherlands, 3Centrum Wiskunde & Informatica, Amsterdam, Netherlands

Synopsis

We present a retrospective rigid motion correction and reconstruction scheme for brain MRI with the aid of structural priors. The proposed framework is designed to be applied to a clinical protocol including multiple scans for multiple contrasts, of which some scans are corrupted due to motion during the acquisitions, but at least one is uncorrupted and exploited as an additional prior. We envision a practical workflow that can easily fit into the existing clinical practice without the need for changing the MRI acquisition protocols.

Introduction

We propose a retrospective technique for the removal of rigid motion artifacts from brain MR reconstructions1,2. The main goal is to provide a post-processing method that can be readily deployed in practical clinical settings (which are mostly based on conventional Cartesian acquisition schemes), with no alterations to the current clinical workflow. We picture the following scenario: in multi-contrast imaging, a trained technician can indicate that some contrasts are severely affected by motion, while other contrasts are deemed acceptable. Instead of repeating the corrupted scan, we propose a technique that aims at improving the contrast most severely affected by motion by leveraging the prior anatomical information provided by the well-resolved contrasts (since they share the same anatomy). Extensive synthetic datasets and a preliminary in-vivo study indicate that the method is potentially mature for multi-slice 2D protocols, and promising for more general 3D acquisition.

Theory

We frame our work in the context of retrospective joint motion correction and reconstruction methods1,2, which can be casted as a constrained bi-level optimization problem:
\begin{equation}\min_{\mathbf{u}\in\mathrm{C},\pmb{\theta}^1,\ldots,\pmb{\theta}^{n_t}}\mathcal{J}(\mathbf{u},\pmb{\theta}^1,\ldots,\pmb{\theta}^{n_t})=\sum_{t}\dfrac{1}{2}\left\lVert\mathcal{S}^t\mathcal{F}[\mathbf{u};\pmb{\theta}^t]-\mathbf{d}^t\right\rVert^2+\mathcal{R}_{\theta}(\pmb{\theta}^1,\ldots,\pmb{\theta}^{n_t}).\end{equation}
Here, the unknowns of interest are the reconstructed image $$$\mathbf{u}$$$ and the rigid motion parameters $$$\pmb{\theta}^t$$$ associated with the $$$t$$$-th readout line (no intra-readout motion is considered). Note that, in this abstract, we only considered 2-D in-plane rigid motion and we perform 2D slice-based reconstruction. The motion-perturbed Fourier transform $$$\mathcal{F}$$$ is defined by
\begin{equation}
\mathcal{F}[\mathbf{u};\pmb{\theta}](\mathbf{k})=\mathrm{NUDFT}[\mathbf{u}](\mathrm{R}_{\pmb{\varphi}}\mathbf{k})\exp{(\mathrm{i}\mathbf{k}\cdot\pmb{\tau})},\quad\pmb{\theta}=(\pmb{\tau},\pmb{\varphi}),
\end{equation}
where $$$\pmb{\tau}$$$ denotes the translation parameters, $$$\mathrm{R}_{\pmb{\varphi}}$$$ is the rotation of the $$$\mathbf{k}$$$-space coordinates about the angles $$$\pmb{\varphi}$$$, and NUDFT is the non-uniform discrete Fourier transform. Despite considering nominal Cartesian sampling, spatial rotations result in effective irregular sampling in the $$$\mathbf{k}$$$-space. The optimization problem is tackled via inexact variable projection schemes3. We employ conventional regularization methods for the motion parameters $$$\mathcal{R}_{\theta}$$$ (although one should consider phase-wrapping issues), and structure-guided TV regularization for image reconstruction4 by defining the constraint set as $$$\mathrm{C}=\{\mathcal{R}_u(\mathbf{u};\mathbf{v})\le\varepsilon\}$$$, where
\begin{equation}
\mathcal{R}_u(\mathbf{u};\mathbf{v})=\left\lVert P(\mathbf{v})\nabla\mathbf{u}\right\lVert_{2,1},\qquad P(\mathbf{v})=\mathrm{I}-\pmb{\xi}(\mathbf{v})\pmb{\xi}(\mathbf{v})^{\mathrm{H}},\quad\pmb{\xi}(\mathbf{v})_i=\dfrac{\nabla\mathbf{v}_i}{\sqrt{|\nabla\mathbf{v}_i|^2+\eta^2}}.
\end{equation}
In this case, $$$\mathbf{v}$$$ represents a known contrast image devoid of motion artifacts. This term enforces the spatial gradient field of $$$\mathbf{u}$$$ to align with the normalized spatial gradient field of $$$\mathbf{v}$$$. We note that the prior and the target contrasts do not need to be co-registered.

Experiment description

We consider the following synthetic examples:
  • numerical BrainWeb5 T1w and T2w phantoms (256x256 images, 1mm$$$^2$$$ in-plane, see Figure 1);
  • in-vivo reconstructions with the following specifications:
    - FOV = 224x224x133.5 mm$$$^3$$$, resolution = 1x1x3 mm$$$^3$$$, slice gap = 1.5mm, slices = 30;
    - T1w: multi-slice Spin Echo, TR/TE = 451/14 ms, flip angle = 70$$$^{\circ}$$$;
    - T2w: multi-slice Turbo Spin Echo, TR/TE = 3400/80 ms, flip angle = 90$$$^{\circ}$$$, TSE factor = 15.
In both these cases, we retrospectively simulate artificial rigid motion artifacts for the T2w contrast and use the T1w contrast as the (uncorrupted) structural prior. The $$$\mathbf{k}$$$-space data is simulated according to nominal Cartesian sampling. The motion type considered here is 2D in-plane "sudden" motion, which consists of two discrete positions where the change of position happens roughly halfway through the scan.
Furthermore, we consider an
  • in-vivo prospective experiment with the following specifications:
    - T1w: Fast Field Echo, FOV = 260x260x260 mm$$$^3$$$, resolution = 2x2x2 mm$$$^3$$$, slice gap = 1 mm, slices = 520, TR/TE = 25/2 ms, flip angle = 30$$$^{\circ}$$$;
    - T2w: multi-slice Fast Field Echo, FOV = 260x260x260 mm$$$^3$$$, resolution = 2x2x2 mm$$$^3$$$, slice gap = 3 mm, slices = 174, TR/TE = 2804/23 ms, flip angle = 18$$$^{\circ}$$$.
    Motion-corruption was induced on the T2w image by instructing the volunteer to replicate 2D in-plane sudden motion, as described previously.
Again, the T1w image is used as prior, and nominal Cartesian sampling is considered.
In Figures 1,2,3 we compare different reconstruction methods:

  • conventional: inverse Fourier transform of corrupted data;
  • joint: joint motion estimation and reconstruction with plain TV regularization;
  • proposed: joint motion estimation and reconstruction with structure-guided TV regularization.

Discussion of the results

The results of the experiments described in the previous section aim at demonstrating the added value of structural priors compared to standard joint motion estimation and reconstruction schemes. These findings are consistent over a wide range of motion types. In particular, we compared a traditional joint estimation method and the proposed technique (the main difference being the use of structure-guided regularization) for sudden motion. We were able to consistently improve on the plain joint reconstruction results by several dB's in PSNR, and several points in SSIM, with higher resolution and fewer motion defects. The gain in resolution can be qualitatively assessed in all the "detail" comparisons in Figures 1,2,3. Some ghosting effects are more effectively removed by structure-guided regularization, as can be seen particularly in Figure 2.

Conclusions

Including structural prior information gleaned from well-resolved contrasts allows a more effective resolution of motion artifacts, which we demonstrated with synthetic and in-vivo studies. In the future, we aim at further assessments of the capabilities of the proposed method with more extensive clinical studies. For a more flexible tool, we will also need to include out-of-plane motion.

Acknowledgements

This publication is part of the project "Reducing re-scans in clinical MRI exams'' (with project number 104022007 of the research program "IMDI, Technologie voor bemensbare zorg: Doorbraakprojecten'') which is financed by The Netherlands Organization for Health Research and Development (ZonMW). The project is also supported by Philips Medical Systems Netherlands BV.

References

  1. Zaitsev, M., Maclaren, J., & Herbst, M. (2015). Motion artifacts in MRI: A complex problem with many partial solutions. Journal of Magnetic Resonance Imaging, 42(4), 887-901.
  2. Godenschweger, F., Kägebein, U., Stucht, D., Yarach, U., Sciarra, A., Yakupov, R., ... & Speck, O. (2016). Motion correction in MRI of the brain. Physics in Medicine & Biology, 61(5), R32.
  3. van Leeuwen, T., & Aravkin, A. Y. (2021). Variable Projection for NonSmooth Problems. SIAM Journal on Scientific Computing, (0), S249-S268.
  4. Ehrhardt, M. J., & Betcke, M. M. (2016). Multicontrast MRI reconstruction with structure-guided total variation. SIAM Journal on Imaging Sciences, 9(3), 1084-1106.
  5. Cocosco, C. A., Kollokian, V., Kwan, R. K. S., Pike, G. B., & Evans, A. C. (1997). Brainweb: Online interface to a 3D MRI simulated brain database. In NeuroImage.

Figures

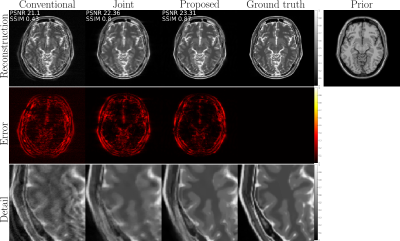
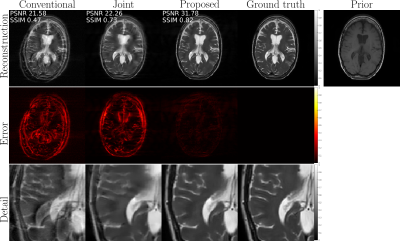
BrainWeb phantom. Reconstruction results for different techniques: (a) conventional = inverse Fourier transform; (b) joint = joint motion estimation and reconstruction with conventional TV regularization; (c) proposed = joint motion estimation and reconstruction with structure-guided TV regularization. PSNR and SSIM metrics are computed after a preliminary rigid registration with the ground truth. The proposed method shows the best results in terms of resolution and artifact removal.

In-vivo data with retrospectively simulated motion artifacts. Reconstruction results for different techniques: (a) conventional = inverse Fourier transform; (b) joint = joint motion estimation and reconstruction with conventional TV regularization; (c) proposed = joint motion estimation and reconstruction with structure-guided TV regularization. PSNR and SSIM metrics are computed after a preliminary rigid registration with the ground truth. The proposed method shows the best results in terms of resolution and artifact removal.


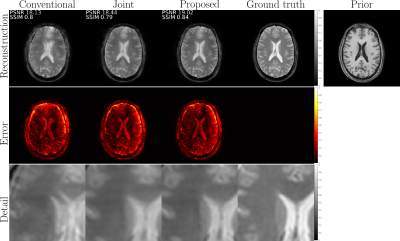
Prospective in-vivo data with motion perturbation induced by deliberate voluntary movement. Reconstruction results for different techniques: (a) conventional = inverse Fourier transform; (b) joint = joint motion estimation and reconstruction with conventional TV regularization; (c) proposed = joint motion estimation and reconstruction with structure-guided TV regularization. PSNR and SSIM metrics are computed after a preliminary rigid registration with the ground truth. The proposed method shows the best results in terms of resolution and artifact removal.


Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)
1957
DOI: https://doi.org/10.58530/2022/1957