Authorship Information

* Denotes equal contribution.

Introduction

Motion frequently corrupts MRI acquisitions, degrading image quality or necessitating repeated scans¹. We demonstrate a deep learning technique for fast retrospective intraslice rigid motion correction in 2D fast spin echo (FSE) brain MRI. In contrast to the existing deep learning retrospective motion correction methods,^2–7 we extend our previously demonstrated architecture that interleaves frequency and image space convolutions. Joint reconstruction outperforms pure image space architectures in the single-coil accelerated acquisition setting⁸. Here we demonstrate advantages of the joint architecture for multicoil, multishot acquisitions.

We assume a quasistatic motion model in which the object remains stationary during individual shots and moves via 2D rotations and translations between shots. We defer modeling through-slice motion effects for future work.

Methods

Data
We demonstrate our approach on k-space data from 2D FLAIR FSE brain MRI scans (3T GE Signa Premier, 48-channel head coil, TR=10000ms, TE=118ms, FOV=260x260mm², acquisition matrix=416x300, slice thickness=5mm, slice spacing=1mm) acquired at our hospital under an approved IRB protocol. We treat the acquired data as ground truth and simulate motion artifacts during training and testing. We split the dataset into 1064 training 2D images (76 subjects), 396 validation images (18 subjects), and 362 test images (17 subjects), with no subject overlap among sets.

Network Architectures and Training
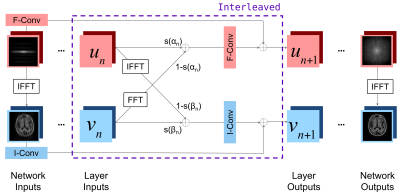
Our joint network learns combinations of frequency and image space features at each layer (Figure 1). The network’s input is an 88-channel image composed of the real and imaginary components of the k-space data from 44 receive coils (4 neck channels from the 48-channel head coil were discarded). The input is processed via 6 successive interleaved layers followed by a single convolution, yielding an 88-channel k-space output converted to the reconstructed image via the inverse Fourier transform and root-sum-of-squares coil combination. We train the network using the structural similarity index measure (SSIM) loss function that compares the reconstruction with the ground-truth, motion-free image.

Motion Simulation
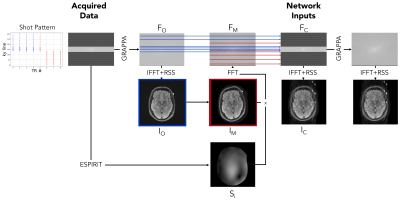
Figure 2 illustrates our motion simulation process. For each image, we select at random a shot at which motion occurs, sample the translation parameters $$$\Delta x$$$ and $$$\Delta y$$$ from a uniform distribution over the range [-10mm,+10mm], and sample the rotation parameter $$$\Delta \theta$$$ from a uniform distribution over the range [-10^o,10^o].

We apply GRAPPA⁹ to the acquired motion-free k-space data $$$F_O$$$, followed by the inverse Fourier transform and root-sum-of-squares coil combination to reconstruct the motion-free image $$$I_O$$$. We estimate coil sensitivity profiles $$$S_i$$$ using ESPIRiT¹⁰ with learned parameter estimation.¹¹

To synthesize the post-movement image $$$I_M$$$, we apply the sampled translation and rotation to $$$I_O$$$. We synthesize the corresponding k-space data that would be acquired by coil $$$i$$$ as $$$F_{M,i} = P\mathcal{F}S_i I_M$$$, where $$$P$$$ is the undersampling operator and $$$\mathcal{F}$$$ is the Fourier transform matrix. Finally, we generate the motion-corrupted k-space data $$$F_C$$$ by interleaving the k-space lines from $$$F_O$$$ and $$$F_M$$$ corresponding to the pre- and post-motion shots, respectively.

We normalize each input and output pair by dividing by the maximum intensity in the corrupted image. Our network reconstructs a normalized version of whichever of $$$F_O$$$ or $$$F_M$$$ corresponds to the position of the subject during acquisition of the central k-space line of $$$F_C$$$.

Implementation Details
We compare the proposed network with baseline architectures composed solely of frequency space convolutions or image space convolutions with twice as many layers as the joint model, such that the total number of convolutions is consistent among all models. We train all networks using the Adam optimizer (learning rate 1e-3) with a batch size of 6. We form each batch using images from the same volume to maintain constant k-space matrix size within a batch. We omit batch normalization when training pure image space networks, as we empirically found it hurt performance. We tune the hyperparameters on the validation set and use the test set for the final evaluation. The networks take 1-3 days to train and 400 milliseconds to run on a new image on an NVIDIA RTX 8000 GPU.

Results and Discussion

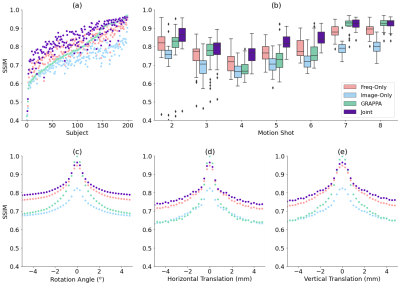
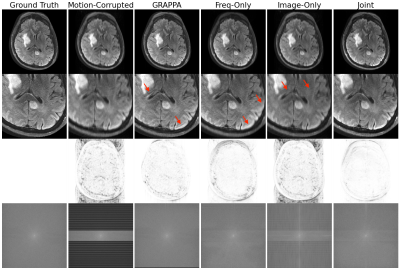
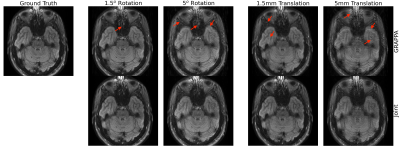
Our method improves over GRAPPA reconstruction of the motion-corrupted k-space data for the majority of subjects and in particular improves images for which GRAPPA performs poorly (Figure 3a). The reconstruction speed is an order of magnitude faster than that of GRAPPA. Our reconstructions outperform the single-space networks for nearly every subject. We also examine reconstruction quality when motion occurs at different shots during the acquisition (Figure 3b) and for varying motion magnitude (Figures 3c-e). Figure 4 illustrates visually that the joint architecture produces sharper, more accurate reconstructions than the GRAPPA baseline and both single-space architectures. Figure 5 shows qualitatively that our method outperforms GRAPPA for severe motions where GRAPPA performs poorly.

Conclusions

We demonstrate a deep learning approach for correcting intraslice rigid motion artifacts in 2D FSE FLAIR MRI and characterize the motion range for which our method succeeds. Future work will extend our approach to model 3D, through-slice motion artifacts and nonrigid motion. Further, we will investigate optimization strategies to ensure consistency of the output with estimated or measured motion parameters. Our technique is a step toward flexible deep learning motion correction for a wide variety of imaging scenarios affected by significant subject motion.

Acknowledgements

Research reported in this abstract was supported in part by GE Healthcare, NIH NIBIB (5T32EB1680, P41EB015896, 1R01EB023281, R01EB006758, R21EB018907, R01EB019956, R01EB017337, P41EB03000, R21EB029641), NIBIB NAC (P41EB015902), NICHD (U01HD087211, K99 HD101553), NIA (1R56AG064027, 1R01AG064027, 5R01AG008122, R01AG016495, 1R01AG070988, RF1AG068261), NIMH (R01 MH123195, R01 MH121885, 1RF1MH123195), NINDS (R01NS0525851, R21NS072652, R01NS070963, R01NS083534, 5U01NS086625, 5U24NS10059103, R01NS105820), and the Blueprint for Neuroscience Research (5U01-MH093765), part of the multi-institutional Human Connectome Project. Additional support was provided by the BRAIN Initiative Cell Census Network grant U01MH117023, and a Google PhD Fellowship.