1920
Parameter Optimization for High-Resolution MR Elastography of the Human Brain at 7T
Emily Rose Triolo1, Oleksandr Khegai2, Jelle Veraart3, Akbar Alipour2, Trey Hedden4, Mehmet Kurt1,2, and Priti Balchandani2
1Mechanical Engineering, Stevens Institute of Technology, Hoboken, NJ, United States, 2Biomedical Engineering and Imaging Institute, Ichan School of Medicine at Mount Sinai, New York City, NY, United States, 3New York University, New York City, NY, United States, 4Ichan School of Medicine at Mount Sinai, New York City, NY, United States
1Mechanical Engineering, Stevens Institute of Technology, Hoboken, NJ, United States, 2Biomedical Engineering and Imaging Institute, Ichan School of Medicine at Mount Sinai, New York City, NY, United States, 3New York University, New York City, NY, United States, 4Ichan School of Medicine at Mount Sinai, New York City, NY, United States
Synopsis
MRE, a technique used to characterize the viscoelasticity of tissues, is typically performed at 3T for the human brain. MRE at 7T has the promise to deliver higher resolution, however, is subject to several artifacts and limitations. Here, we developed and tested an MRE setup and sequence at 7T on one subject at three different resolutions to investigate how both changing resolution and using MP-PCA denoising affects the estimated shear modulus (|G*|). Our pilot study has shown an increase in OSS-SNR after using MP-PCA denoising, and has demonstrated a relationship between resolution, OSS-SNR, and |G*| that requires further investigation.
Introduction
Magnetic resonance elastography (MRE) is a technique for determining the mechanical response of tissues using applied harmonic deformation and motion-sensitive MRI1. Studies using MRE to investigate the mechanical properties of the human brain are most commonly performed at conventional field strength (3 Tesla (T) or 1.5T), although there have been a few attempts at the ultra-high field strength, 7T2,3. Aiming for higher resolution at 7T, MRE presents unique challenges of decreased SNR and lower shear wave motion sensitivity. Additionally, it has been shown that quantitative values of MRE, i.e. the magnitude of the complex shear modulus estimate (|G*|), are sensitive to changes in SNR4, so 7T MRE can present a challenge of not only quality but accuracy. While commonly-used filtering techniques (e.g., Gaussian, Median) can increase the SNR of MRE phase data (to combat low SNR in high-resolution scans), this also can blur fine physiological features, decrease the effective resolution5, resulting in artificially increased |G*|4. By utilizing a Marchenko-Pastur Principal Component Analysis (MP-PCA) denoising algorithm, and exploiting the intrinsic redundancies in MRE acquisition, physiological structures can be preserved, and high resolutions can be maintained5. In MP-PCA denoising, using redundancies in slice acquisition and the universal properties of the eigenspectrum of random covariance matrices, the noise-only principal components identified and removed. Thereby, one increases precision and SNR without compromising accuracy and spatial resolution5. The purpose of this study is to conduct a pilot investigation into the effect of changing resolutions and utilization of a MP-PCA-based denoising algorithm on the magnitude of the complex shear modulus estimate of the human brain.Methods
Full brain coverage MRE was performed on one healthy human subject at 1.7mm, 1.3mm, and 1.1mm isotropic resolutions at 50Hz vibration frequency, using a 32-channel head coil (Nova Medical) on a 7T Siemens Magnetom MRI Scanner. The designed MRE sequence (Figure 1a) was a modified single-shot multi-slice spin-echo 2D-EPI sequence with trapezoidal flow-compensated motion encoding gradients (MEGs)6, synchronized with the acoustic actuator (Figure 1b)7 by TTL triggering at the beginning of every TR (TR/slice=140ms, TE=65ms, GRAPPA=3). Images were masked using BET (Brain Extraction Tool) of FSL package8, denoised using a MP-PCA algorithm5, and unwrapped using a Laplacian-based technique9. Curl filtering, Fourier decomposition, and a quartic smoothing kernel (scaled for resolution based on our previous investigation7) were used to acquire wavefield images, before Algebraic Inversion of the Helmholtz Equation was used to calculate the complex shear stiffness10. We then calculated the average octahedral shear strain-based signal-to-noise (OSS-SNR) for both original and denoised displacement data at each resolution11.Results
7T MRE sequence has been developed and validated previously for accurate estimation of |G*| in phantom experiments at different resolutions7. We have also determined that, for our linearly elastic phantom, there is no inherent difference in |G*| when the field strength is changed from 3T to 7T (matching resolutions), nor when resolution is changed within 7T7,12. Using these preliminary results, our post-processing techniques were verified, so elastograms showing a central slice of the brain are shown for each of the three resolutions to demonstrate the differences in the magnitude of the complex shear modulus (|G*|) and in feature resolution (Figure 2). Additionally, the OSS-SNR values for each dataset are listed in Table 1, with a central slice map showing the difference between original and denoised 1.1mm displacement data in terms of OSS-SNR (Figure 3).Discussion
Based on the whole-brain stiffness estimates (|G*|) and SNR values, within-resolutions, denoising using the MP-PCA algorithm substantially increases the OSS-SNR and therefore affects |G*|. The benefit of using PCA-based denoising as opposed to other filtering techniques is that denoising maintains the physiological structures within the human brain and helps prevent over-smoothening/overfitting. This increased accuracy and sensitivity is of particular importance for smaller brain features, for example, the hippocampus when investigating changes due to Alzheimer’s disease or dementia. However, there appears to be a more complex relationship between OSS-SNR and |G*| between resolution likely due to the post-processing steps taken between displacement calculation and stiffness estimation. Additionally, the 1.7mm resolution scan appears to have an overall higher average |G*| than the 1.3mm and 1.1mm resolution scans, somewhat matching the increase in OSS-SNR values, which can be confirmed with further replicates. This potentially implies that additional fine viscoelastic features are detected at higher resolutions, decreasing the wavelength-based stiffness estimate, supporting the hypothesis of Barnhill, et al.3. Overall, to better understand these trends, we will continue to perform MRE at 7T on healthy human subjects at these three representative resolutions to better characterize the effects of both differing resolutions, change in field strength (3T versus 7T), and denoising on complex stiffness estimations of the human brain.Conclusion
In conclusion, our pilot study has shown a substantial increase in OSS-SNR after the use of MP-PCA denoising algorithm on the complex displacement data generated during MRE at 7T, and has shown a relationship between resolution, OSS-SNR, and |G*| that requires further investigation with a larger cohort of subjects.Acknowledgements
The authors would like to acknowledge equal contribution from Emily Triolo and Oleksandr Khegai as co-first authors, and Mehmet Kurt and Priti Balchandani as co-final authors. The authors would also like to acknowledge the support from NSF CMMI 1953323 and NIH funding R21AG071179.References
1. J. F. Greenleaf, R. Muthupillai, P. J. Rossman, J. Smith, A. Manduca, and R. L. Ehman, “Direct Visualization of Strain Waves by Magnetic Resonance Elastography (MRE),” in IEEE Ultrasonics Symposium, 1996, pp. 467–472.2. J. Braun et al., “High-resolution mechanical imaging of the human brain by three-dimensional multifrequency magnetic resonance elastography at 7T,” Neuroimage, vol. 90, pp. 308–314, 2014, doi: 10.1016/j.neuroimage.2013.12.032.
3. E. Barnhill et al., “Impact of Field Strength and Image Resolution on MRE Stiffness Estimation,” in Proc 24th Annual Meeting ISMRM, 2016.
4. Murphy, M. C., Huston, J., 3rd, Jack, C. R., Jr, Glaser, K. J., Senjem, M. L., Chen, J., Manduca, A., Felmlee, J. P., & Ehman, R. L. (2013). Measuring the characteristic topography of brain stiffness with magnetic resonance elastography. PloS one, 8(12), e81668. https://doi.org/10.1371/journal.pone.0081668
5. J. Veraart, D. S. Novikov, D. Christiaens, B. Ades-aron, J. Sijbers, and E. Fieremans, “Denoising of diffusion MRI using random matrix theory,” Neuroimage, vol. 142, pp. 394–406, 2016, doi: 10.1016/j.neuroimage.2016.08.016.
6. C. A. Chaze et al., “Altered brain tissue viscoelasticity in pediatric cerebral palsy measured by magnetic resonance elastography,” NeuroImage Clin., vol. 22, 2019, doi: 10.1016/j.nicl.2019.101750.
7. E. R. Triolo, O. Khegai, A. Alipour, P. Kennedy, P. Balchandani, and M. Kurt, “Validation and testing of 7T MR elastography sequence and stiffness reconstruction,” in BMES 2021, 2021.
8. M.W. Woolrich, S. Jbabdi, B. Patenaude, M. Chappell, S. Makni, T. Behrens, C. Beckmann, M. Jenkinson, S.M. Smith. Bayesian analysis of neuroimaging data in FSL. NeuroImage, 45:S173-86, 2009
9. M. A. Herraez, D. R. Burton, M. J. Lalor, and M. A. Gdeisat, "Fast two-dimensional phase-unwrapping algorithm based on sorting by reliability following a noncontinuous path", Applied Optics, Vol. 41, Issue 35, pp. 7437-7444 (2002).
10. T. E. Oliphant, A. Manduca, R. L. Ehman, and J. F. Greenleaf, “Complex-valued stiffness reconstruction for magnetic resonance elastography by algebraic inversion of the differential equation,” Magn. Reson. Med., vol. 45, no. 2, pp. 299–310, 2001, doi: 10.1002/1522-2594(200102)45:2<299::AID-MRM1039>3.0.CO;2-O.
11. M. D. J. McGarry, E. E. W. Van Houten, P. R. Perrĩez, A. J. Pattison, J. B. Weaver, and K. D. Paulsen, “An octahedral shear strain-based measure of SNR for 3D MR elastography,” Phys. Med. Biol., vol. 56, no. 13, 2011, doi: 10.1088/0031-9155/56/13/N02.
12. E. Triolo et al., “Development and validation of an ultra-high field compatible MR elastography actuator,” in Summer Biomechanics, Bioengineering and Biotransport Conference, 2021, p. SB3C2021-325.
Figures
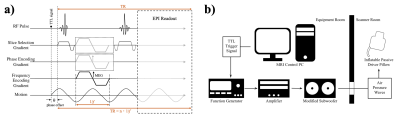
Figure 1: a) The designed 2D EPI multi-slice MRE sequence diagram with 3D motion encoding gradients, labeled with the trigger (TTL) signal, phase offset, vibration period, and TR labeled. b) The custom-designed MRE Hardware and triggering setup where a TTL trigger signal during acquisition drives the signal generator, amplifier, and subwoofer via external triggering, pushing air pressure waves through rubber tubing and into the tissue-contacting end-effector.
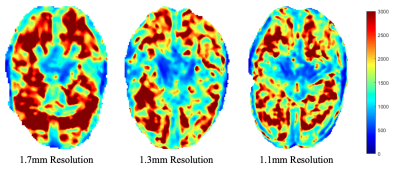
Figure 2: Elastograms showing magnitude of the complex shear modulus (|G*|) in Pa at three representative isotropic resolution.
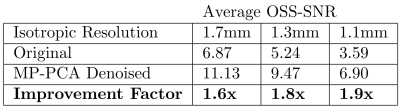
Table 1: Average OSS-SNR value of the whole brain at three representative resolutions before and after MP-PCA denoising
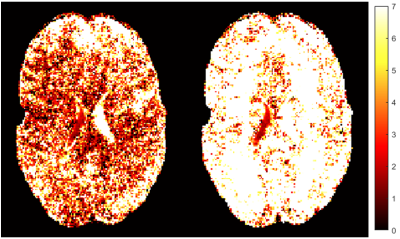
Figure 3: OSS-SNR map comparison between original (left) and MP-PCA denoised (right) data at 1.1mm resolution
DOI: https://doi.org/10.58530/2022/1920