1905
Design and Optimization of Asymmetrical Tapered RF Solenoid Tx / Rx Coil for Halbach-Array based Low-field MRI Scanner1Singapore University of Technology, Singapore, Singapore
Synopsis
The optimization of an asymmetrical tapered solenoid coil using multi-objective Genetic Algorithm is presented to achieve high sensitivity, high homogeneity, low inductance simultaneously at 2.84MHz within a cylindrical volume(95×95х10mm). The asymmetrical solenoid coil has a lower half that consists of turns with variable pitches and a constant radius and an upper half that consist of turns with variable pitches and profile curvature(variable radius). Two coil winding patterns are included: single winding and multiple windings at each groove. The optimal design shows a sensitivity of 138 μT/√W (29.7%increase), 3.8% homogeneity reduction, comparable inductance compared to a traditional solenoid of similar dimensions.
Introduction
The development of Low-field Halbach-array based MRI scanners with inhomogeneous [1] and homogeneous [2] B0 field necessitates the choice of solenoidal RF coils due to its vertical B0 direction. To compensate the reduced Signal-to-Noise Ratio (SNR) due to lower field strength in such scanners, RF coils with high sensitivity and high homogeneity are necessary. A regular solenoid coils that are designed to have a high and homogeneous B1 field normally has a large inductance which results in long ring down time. In the design of solenoid RF coils, with an increase in the size of the field of view (FoV), an increase in sensitivity without trade-off in inductance and homogeneity is a challenging aspect. In the literature, the improvement in homogeneity from the optimization of pitch of each turn of cylindrical solenoid [2] and the winding pattern of head shaped RF solenoid coil [3] has been reported for their respective FoV and application under consideration. The improvement is at the cost of reduction in average B1 field (the former) and increase in inductance (the latter). There is a need to further design and optimize a solenoid considering all the above contradicting objectives. Hence, we propose an approach, the design and optimization of an asymmetrical tapered solenoid coil using multi-objective Genetic Algorithm (GA) to achieve high sensitivity without having a high inductance or compromising the homogeneity.Methods
The asymmetrical tapered solenoid coil consists of two sections: 1) lower half (cylindrical) consisting of turns with variable pitches & a constant radius, and 2) upper half (Tapered) consisting of turns with variable pitches and a variable profile curvature, i.e., variable radius, as shown in Fig. 1. For a coil with total number of turns (N), the design variables are the number of turns in lower half section (Ns), the profile curvature of tapering (C) and the pitch of each turn (pi [i = 1 to N]) .Multi-objective GA was used for optimization. Fig.2 shows the flow of the algorithm. The optimization objectives are 1) B1avg ≥ 0.25 mT 2) D ≤ 0.02 mT 3) Minimize L, where B1avg is the average field and D is the difference between the maximum and the minimum field in the targeted 3D cylindrical FoV (95 × 95 х 10 mm), L are the self-inductance of the solenoid coil. They are designed to obtain a high field strength, high homogeneity, and a low inductance, respectively. The total number of turns, N, was preset to be 20, 45 & 90, which covers the minimum and maximum possible range for a 180 mm length coil wound with 1mm wire diameter. The size of the population was set to be 200. B1avg was calculated using Biot-Savart’s law, L is obtained based on the numerical integration of the Neumann formula [4].
The design frequency of the coil is 2.84 MHz. The optimization is considered using two methods with different winding patterns, single turn (Method I: M-I) and multiple turns (Method II: M-II) at each groove. Matlab was used for the implementation.
Results and Discussions
The Best and Average fitness of each objective function during the evolution of generations is plotted in Fig. 3. The plots of objective 1 varying with objective 2 & 3 of the obtained pareto-optimal solutions are shown in Fig. 4. The above plots are shown for N = 45 optimization. The pareto-solutions obtained from N= 20, 45 & 90 for M-I and M-II optimisations are compared and the best candidate with high B1avg satisfying the required homogeneity with the least inductance is obtained which is M-I optimized coil of N = 45. The wire traces of the reference standard solenoid coil and that of the optimized ones using M-I & M-II with their B1 field distributions on three slices at z = 0, -5mm & -10mm is shown in Fig 5. A, B and C, respectively. Fig.5D tabulates the performances of these three solenoids.In Fig. 5., the optimized coil of M-I shows a B1avg sensitivity, inductance & homogeneity of 0.33 mT, 138 μT/√W, 93.17 μH & 92.70%, respectively. It is an increase of 29.7% in B1avg a 3.8% reduction in homogeneity and comparable L compared to the reference solenoid. The optimized coil of M-II shows improvement of 43% of B1avg at the cost of 62.5% & 26% traded-off with inductance &homogeneity respectively. The optimized results show that the single turn winding has the possibility of obtaining a better combination among the field strength, inductance, and field homogeneity compared to the multiple turns winding method for a solenoid. The bandwidth of the design is comparable to the reference solenoid, which makes it suitable for a Halbach system when B0 is more homogeneous.
It is a preliminary design and optimization on a high-performance solenoid for low-field MRI. A good balance of coil sensitivity, field homogeneity, and coil inductance is obtained using the proposed coil configuration and the single turn wire winding method. It is a showcase using a relatively small FoV. Moving forward, better designs as well as better optimization approaches for RF coils for a Halbach MRI system need to be sought, especially considering the B0 field inhomogeneity of such a system where wide bandwidth of an RF coil is needed.
Acknowledgements
No acknowledgement found.References
[1] Ren, Zhi Hua, et al. "A low-field portable magnetic resonance imaging system for head imaging." 2017 Progress in Electromagnetics Research Symposium-Fall (PIERS-FALL). IEEE, 2017.
[2] O'Reilly, T., W. M. Teeuwisse, and A. G. Webb. "Three-dimensional MRI in a homogenous 27 cm diameter bore Halbach array magnet." Journal of Magnetic Resonance 307 (2019): 106578.
[3] Ren, Zhi Hua, and Shao Ying Huang. "The design of a short solenoid with homogeneous B1 for a low-field portable MRI scanner using genetic algorithm." poster, ISMRM 26th Annual Meeting & Exhibition. 2018.
[4] Shen, Sheng, et al. "Optimization of a Close-Fitting Volume RF Coil for Brain Imaging at 6.5 mT Using Linear Programming." IEEE Transactions on Biomedical Engineering 68.4 (2020): 1106-1114.
[5] Dengler, Richard. "Self inductance of a wire loop as a curve integral." arXiv preprint arXiv:1204.1486 (2012).
Figures
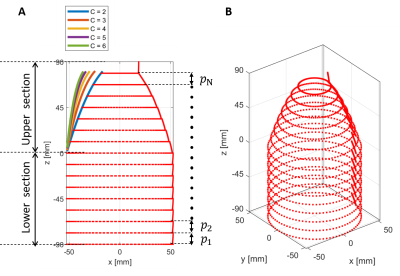
Figure 1. Illustration of the tapered asymmetrical solenoid coil geometry. A) Side view showing the asymmetrical upper and lower half sections B) 3D view. Design parameters: Total number of turns (N), number of turns in lower half section (Ns), profile curvature of tapering (C) and pitch of each turn (pi [i = 1 to N]).The diameter of the cylindrical portion of the coil and that of the wire is 105 mm and 1mm respectively.
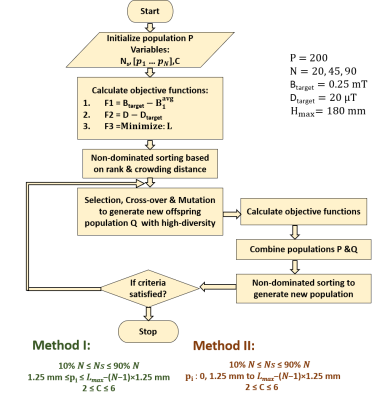
Figure 2. Flow-chart of GA multi-objective optimization algorithm to optimize NS (No. of turns in lower section of the solenoid), pi [i = 1..N] (pitch of each turn i) and C (curvature/tapering profile) for N = 20, 45 & 90 using two methods with different winding pattern of the coil. In Method I and II, the coils can have single and multiple turns at each pitch level respectively. The number of populations and maximum generation in the optimization is set as 200 & 200 respectively.

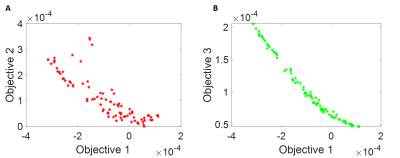

Figure. 5. Current path of the coil , B1 distribution at planes z = 0, z = -5 mm, z = -10 mm (corresponding to 3D FoV: 95 × 95 × 10 mm) from left to right of A) standard solenoid coil with same N = 45, coil diameter = 105 mm, Length = 180 mm, B) Method-I Optimized coil for N =45, C) Method-II Optimized coil for N =45, D) Summary of performance metrics of the above coils. B1avg is the average field and D is the difference between the maximum and the minimum in the respective 2D FoV (95 × 95 ×10) mm.