Introduction

Radio frequency (RF) pulses play a key role in magnetic resonance imaging. While current clinical MRI systems use pre-defined RF waveforms with minimal adaptions, multidimensional spatial-selective RF pulses have many applications in MR imaging for restricting the field of view (FOV) to improve the resolution and reduced geometry distortion. The two-dimensional RF pulse design given a desired spatial excitation profile is an inverse problem not guaranteed to have analytical solutions. The Shinnar–Le Roux (SLR) algorithm¹ was proven to handle any flip angle from 0° to 180°, but it is time-consuming and not appropriate for real-time waveform generation. A recent study has introduced convolutional neural network (CNN) to achieve fast 2D RF pulse designs with excellent performance². In this work, we target on a more robust and faster RF estimations for any rectangle excitation profiles, and propose a hybrid framework to combine CNN with signal modeling by feature extractions.

Methods

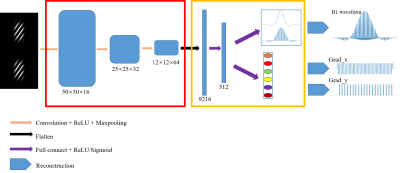
The RF pulse signals were modeled based on their signal shape features. For B1 waveforms $$$b_{RF}$$$, since it comprised short trains of RF sub-pulses with the same shape but unique amplitudes and phases ^3,4, each $$$b_{RF}$$$ were decomposed to a sinc-like basis function $$$b_{base}$$$ as basis convoluted with a series of sub-pulse functions $$$b_{sub}$$$ with different amplitudes as weights: $$$b_{RF}=b_{base}\otimes b_{sub}$$$, where $$$\otimes$$$ represented signal convolution. For the gradient waveforms in frequency direction Gx and in phase direction Gy on an echo-planar trajectory, the blipping gradients occur at the time of rising edge in Gx (except for the first blip), and the periods of Gx and Gy were equal, with 180° phase difference. As a result, each pair of Gx, Gy were represented by 6 parameters: 1) the start time of Gx; 2) the number of sub-pulses of Gx; 3) the period of Gx; 4) the amplitude of Gx; 5) the amplitude of Gy and 6) the duration of each sub-pulse of Gy.
The hybrid deep learning framework containing the above signal modeling was shown in Figure 1, with two parts represented by blocks in red box and yellow box, respectively. The first part in the red box was created using the generalized CNN architecture². The second part in the yellow box contained flattening layers to flatten and transform the 2D features to a vector of 512, which was fully connected to the output layers. The output signals were reconstructed using our proposed signal modeling. Bloch simulation was applied on the reconstructed RF signals to present the resulting 2D excitation profiles.
Nine thousand sets of RF and gradients with 2-dimensional random rectangle spatial selectivity (90° flip angle) were generated as dataset using the SLR method¹. 90% of the data were used as training set and 10% as testing set. The hybrid model was compared with the SLR-based simulation (as gold standard) and the generalized CNN based model² (as baseline) on each components of the RF pulse signals and the resulting excitation profiles. Normalized root mean square error (nRMSE) was calculated for RF pulse signals and the excitation profiles.

Results

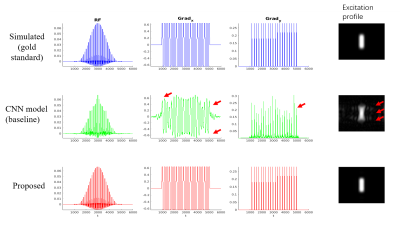
Figure 2 demonstrates a typical case of predicted RF and gradient waveforms (Gx, Gy) by the baseline model with generalized CNN framework (in green) and our proposed model with hybrid framework (in red), along with the SLR simulated waveforms (in blue). The corresponding excitation profiles were also shown. A noticeable mismatch (red-arrowed) was observed between the signal from CNN model and the simulated data in all three signals, and contaminated excitation areas were also observed on the corresponding profile. The proposed method yielded accurate estimation results compared to the simulated data. Table 1 showed the nRMSE of the RF signals and the corresponding 2D excitation profiles with comparisons between the baseline method and the proposed model. The decreased nRMSE using hybrid model indicated a more accurate and robust estimation. The average computation time for predicting one RF case was ~3ms, reduced by approximately a factor of 43 compared to the baseline method (~130ms).

Discussion and Conclusion

In this work, we propose to analytically represent the RF signals using a small number of parameters, which effectively reduce the number of output layer neurons from 6000*3 (for baseline method) to 306 neurons, hence, reducing the complexity of the CNN neural network without losing information. This is also beneficial for reducing the risk of overfitting. The analytical signal representation ensures an accurate RF signal reconstruction, and therefore is potentially practical for on-the-fly RF pulse design estimation.

Acknowledgements

No.