1859
Accelerated Magnetic Resonance Imaging with Flow-Based Priors1Department of Electrical and Computer Engineering, Technical University of Munich, Munich, Germany, 2Department of Electrical and Computer Engineering, Rice University, Houston, TX, United States
Synopsis
Convolutional neural networks trained end-to-end achieve state-of-the-art image quality for accelerated MRI. But end-to-end networks are trained for a specific undersampling operator. A more flexible approach that can work with any undersampling operator at inference is to train a generative image prior and impose it during reconstruction. In this work, we train a flow-based generator on image patches and then impose it as a prior in the reconstruction. We find that this method achieves slightly better reconstruction quality than state-of-the-art un-trained methods and slightly worse quality than neural networks trained end-to-end on the 4x accelerated multi-coil fastMRI dataset.
Introduction
Convolutional neural networks trained end-to-end to reconstruct an image from undersampled MRI measurements achieve excellent imaging performance1,2,3. But these methods make assumptions about the undersampling operator during training and thus require retraining when the sampling pattern or the acceleration factor changes.Bora et al.4 proposed a more flexible approach for reconstructing a signal from few measurements: Train a generative model and optimize over the range of the generator during reconstruction. Bora et al.4 originally trained a generative adversarial network as a prior. Jalal et al.5 used score-based generative models and Asim et al.6 found invertible neural networks (INNs) to work well for image reconstruction problems.
However, imposing an invertible prior has not been adapted to real-world medical imaging tasks. In this work, we train a flow-based generator on patches of MR images and then impose it as a prior for reconstructing an MR image from undersampled multi-coil measurements.
Methods
We use flow-based generators as an image prior for accelerated MRI. Flow-based generators are generative models that enable exact and efficient log-likelihood evaluation and efficient image synthesis7,8. Specifically, we use Glow9, since it has a simple architecture and achieves good image quality on standard benchmarks for generative models.We train a Glow-generator by directly minimizing the negative log-likelihood of image patches. There are two main motivations for training the prior on patches rather than full images. First, training on patches reduces the computational and memory cost. Second, a patch-based prior enables us to recover images of arbitrary shapes10.
We train the prior on mid-slice images from the fastMRI multi-coil knee training set11. We obtain the image patches used for training in three steps. First, we reduce a spatially resolved multi-coil image into a single complex-valued image using estimates of the sensitivity maps. Second, we normalize the image. Third, we random crop to obtain image patches. Note that we do not make any assumptions about the undersampling mask. Hence, a single trained prior can be used for different sampling patterns and undersampling ratios.
Once trained, we impose the flow-based generator as a prior when recovering an image from undersampled measurements. In order to reconstruct an image, we minimize a loss function that enforces data consistency with the known frequencies of the undersampled k-space. We regularize the optimization problem implicitly by starting with the most likely image under our prior. Additionally, our reconstruction loss explicitly penalizes latent representations with a large Euclidean norm, i.e., images with low likelihood. Our formulation of the loss is based on4,6,12,13.
Results
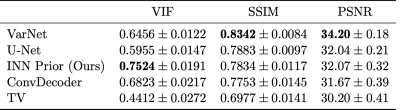
We evaluate the in-distribution performance of our method on the fastMRI knee validation set and measure its robustness to distribution shifts by testing on other datasets as well. We measure image quality in terms of peak signal-to-noise ratio (PSNR), structural similarity index (SSIM)14 and visual information fidelity (VIF)15. We use the root-sum-of-squares (RSS) image16 obtained from fully sampled data as the ground truth for our comparisons.We start with evaluating the in-distribution performance on the 4x accelerated multi-coil mid-slice images of all 199 volumes in the fastMRI validation set. Table 1 shows the results obtained with our method compared to trained and un-trained methods. For VarNet2, U-Net1, ConvDecoder12 and total variation (TV) regularization17 we use the results from12.
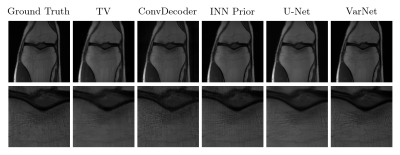
The method achieves the best VIF scores of all evaluated methods, but is outperformed by end-to-end trained methods (VarNet and U-Net) according to SSIM. Our method obtains slightly higher scores than ConvDecoder, the state-of-the-art un-trained method. Furthermore, our method significantly outperforms TV. Figure 1 shows sample reconstructions for a 4x accelerated measurement from the fastMRI knee validation set.
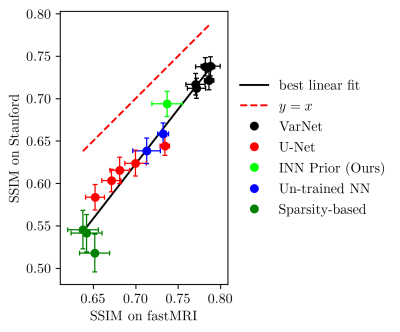
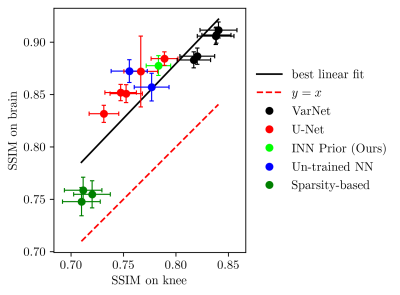
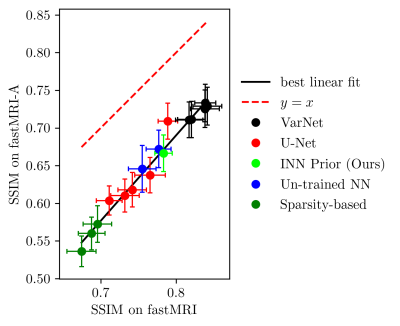
Next, we study the robustness to distribution shifts. Following Darestani et al.18, we evaluate the performance under three distribution shifts: The dataset shift to the Stanford knee dataset18, the anatomy shift to the fastMRI brain dataset and the adversarially-filtered shift to the fastMRI-A dataset18. We refer to18 for details of the experimental setup.
Figures 2 to 4 show the results. We observe that our prior-based method loses a similar amount of performance as the other methods when reconstructing images from the Stanford and fastMRI-A dataset. This result is in line with the findings of Darestani et al.18, who observed a linear relationship between in-distribution and out-of-distribution performance for trained and un-trained methods, similar to what has been observed for classification problems in19,20. Furthermore, our method achieves higher SSIM scores on the brain dataset than on the knee dataset, even when trained only on knee images. As Darestani et al.18 noted, this effect comes from the fact that brain images are naturally easier to reconstruct.
Discussion and Conclusion
In this work, we applied flow-based priors to the problem of accelerated multi-coil MRI. The method provides flexibility as the undersampling operator can change during inference. The method outperforms the best un-trained methods that enable the same flexibility. However, it is outperformed by end-to-end trained methods like VarNet which require retraining when the undersampling operator changes. Furthermore, our method loses a similar amount of performance under distribution shifts as trained and un-trained methods, and is therefore no less or no more sensitive to distribution shifts than other methods.Code
Code is available at https://github.com/ffraaz/flow_based_priorsAcknowledgements
We thank Mohammad Zalbagi Darestani for providing us with a VarNet checkpoint and the scores for VarNet, U-Net, ConvDecoder and TV used in Figures 2 to 4.References
1. O. Ronneberger, P. Fischer, and T. Brox. “U-Net: Convolutional networks for biomedical image segmentation”. In: arXiv:1505.04597 (2015).
2. A. Sriram, J. Zbontar, T. Murrell, A. Defazio, C. L. Zitnick, N. Yakubova, F. Knoll, and P. Johnson. “End-to-end variational networks for accelerated MRI reconstruction”. In: arXiv:2004.06688 (2020).
3. P. Putzky and M. Welling. “Invert to learn to invert”. In: Advances in Neural Information Processing Systems. 2019.
4. A. Bora, A. Jalal, E. Price, and A. G. Dimakis. “Compressed sensing using generative models”. In: International Conference on Machine Learning. 2017, pp. 537–546.
5. A. Jalal, M. Arvinte, G. Daras, E. Price, A. G. Dimakis, and J. I. Tamir. “Robust compressed sensing MRI with deep generative priors”. In: Advances in Neural Information Processing Systems. 2021.
6. M. Asim, M. Daniels, O. Leong, A. Ahmed, and P. Hand. “Invertible generative models for inverse problems: Mitigating representation error and dataset bias”. In: International Conference on Machine Learning. 2020, pp. 399–409.
7. L. Dinh, D. Krueger, and Y. Bengio. “NICE: Non-linear independent components estimation”. In: International Conference on Learning Representations. 2015.
8. L. Dinh, J. Sohl-Dickstein, and S. Bengio. “Density estimation using real NVP”. In: International Conference on Learning Representations. 2017.
9. D. P. Kingma and P. Dhariwal. “Glow: Generative flow with invertible 1x1 convolutions”. In: Advances in Neural Information Processing Systems. 2018.
10. R. Anirudh, S. Lohit, and P. Turaga. “Generative patch priors for practical compressive image recovery”. In: arXiv:2006.10873 (2020).
11. J. Zbontar et al. “fastMRI: An open dataset and benchmarks for accelerated MRI”. In: arXiv:1811.08839 (2019).
12. M. Z. Darestani and R. Heckel. “Accelerated MRI with un-trained neural networks”. In: arXiv:2007.02471 (2021).
13. V. A. Kelkar, S. Bhadra, and M. A. Anastasio. “Compressible latent-space invertible networks for generative model-constrained image reconstruction”. In: IEEE Transactions on Computational Imaging (2021), pp. 209–223.
14. Z. Wang, A. Bovik, H. Sheikh, and E. Simoncelli. “Image quality assessment: From error visibility to structural similarity”. In: IEEE Transactions on Image Processing (2004), pp. 600–612.
15. H. Sheikh and A. Bovik. “Image information and visual quality”. In: IEEE Transactions on Image Processing (2006), pp. 430–444.
16. P. B. Roemer, W. A. Edelstein, C. E. Hayes, S. P. Souza, and O. M. Mueller. “The NMR phased array”. In: Magnetic Resonance in Medicine (1990), pp. 192–225.
17. K. Block, M. Uecker, and J. Frahm. “Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint”. In: Magnetic Resonance in Medicine (2007), pp. 1086–1098.
18. M. Z. Darestani, A. S. Chaudhari, and R. Heckel. “Measuring robustness in deep learning based compressive sensing”. In: International Conference on Machine Learning. 2021, pp. 2433–2444.
19. B. Recht, R. Roelofs, L. Schmidt, and V. Shankar. “Do ImageNet classifiers generalize to ImageNet?” In: International Conference on Machine Learning. 2019, pp. 5389–5400.
20. R. Taori, A. Dave, V. Shankar, N. Carlini, B. Recht, and L. Schmidt. “Measuring robustness to natural distribution shifts in image classification”. In: Advances in Neural Information Processing Systems. 2020, pp. 18583–18599.
Figures