1858
Development of Non-Rectangular Excitation Pulses for Improved kZ Fidelity in Super-Resolution T2-Weighted Spin-Echo MRI
Eric Allen Borisch1, Alexandru C. Florea1,2, Roger C. Grimm1, Akira Kawashima3, and Stephen J. Riederer1
1Radiology, Mayo Clinic, Rochester, MN, United States, 2Gustavus Adolphus College, Saint Peter, MN, United States, 3Radiology, Mayo Clinic, Phoenix, AZ, United States
1Radiology, Mayo Clinic, Rochester, MN, United States, 2Gustavus Adolphus College, Saint Peter, MN, United States, 3Radiology, Mayo Clinic, Phoenix, AZ, United States
Synopsis
Results from continuing investigation of non-rectangular slice excitation profiles with the goal of providing improved results when used to reconstruct overlapping-slice 2D acquisitions leveraging knowledge of the slice profile are presented. A simulation of the excitation/acquisition process and accompanying reconstruction has been developed to aid the exploration of non-traditional slice profiles and their impact on the final reconstruction quality.
Introduction
There is growing contemporary interest in addressing the limited (≈3 mm) through-plane resolution in 2D acquisitions1-3. Sufficiently improved through-plane resolution in one (e.g. axial) orientation may allow multiplanar reformats in other (sagittal, coronal) orientations, obviating direct acquisition in those orientations. One approach is to acquire overlapped slices and correct for the slice profile, a process we refer to as $$$k_Z$$$-space based multislice (KZM) reconstruction3. We have previously shown that the traditional rectangular (rect) excitation pulse causes zero crossings in the $$$k_Z$$$ passband of interest, preventing accurate recovery of signal at those frequencies. We have subsequently shown in resolution phantoms how alternative excitations (e.g. Gaussian, raised-cosine) preserve signal power at these frequencies4. The purpose of this work is to study the resolution and SNR aspects of such pulses in more detail, with the targeted application of prostate T2SE MRI.Methods
Axial excitation was assumed with slice selection (Z) along the superior/inferior (S/I) direction. Three RF profiles were considered: (i) the experimentally measured 3 mm thick rect; (ii) Gaussian; (iii) raised cosine ($$$rCos = \frac{1}{2}\left(1+cos(\frac{\pi k_Z}{k_C})\right)$$$ for $$$|k_Z| \le k_C$$$, 0 otherwise, $$$k_C$$$ tunable). Gaussian and rCos were tuned to have 3 mm thick excitation, defined as 5% response at $$$k_Z = 1/(3 mm)$$$. Figure 1 shows the $$$k_Z$$$ responses of these profiles, illustrating the zero crossing of the rect and monotonically decreasing behavior of Gaussian and rCos. The effects of slice profile were studied with simulation and experimental measurement.Performance of the axial through-plane, resolution-enhancing reconstruction was assessed in the sagittal plane. For simulation, a natively acquired sagittal image was used, resampled to the desired S/I resolution to provide the input target signal. Next, the simulation imposed onto the target signal via convolution the (complex) slice excitation profile being studied after which Gaussian noise was added at a prescribed level (scaled relative to signal power) to generate the simulated acquired signal. This was sampled at the prescribed slice sampling rate. The simulated acquired signal is expected to have similar characteristics to a sagittal reformat of a native axial signal acquired utilizing the same slice profile. Next, the simulated acquired signal was passed through the reconstruction process3 to generate the (sagittal) reconstructed signal, which could then be compared to the target signal. Ideally the reconstructed signal matches the target signal with no more than the intentionally added noise as a difference. Results from simulation were also compared with sagittal reformats from axial acquisition with and without the resolution-enhancing reconstruction.
The linear reconstruction uses Tikhonov regularization which has input parameter $$$\lambda$$$ to trade off noise with edge recovery performance. In the simulation the optimum $$$\lambda$$$ was taken as that value providing minimum mean square error (MMSE) in the difference between the target and reconstructed signals.
The three excitation profiles have slightly different (±10%) areas along Z and thus slightly different relative SNRs in the assumed acquired measurements. This was accounted for in the simulation by scaling the added noise to provide a fair comparison between profiles.
Results
Figure 2 shows a native sagittal input image (A), the simulated acquired (B) and reconstructed signal (C) assuming the measured 3mm-thick slice excitation profile and 1 mm slice-to-slice increment, and sagittal reformats of experimentally acquired axial images without (D) and with (E) the resolution-enhancing filter. The acquisition for (D) used the 3 mm thick rect excitation with 1 mm increment assumed for (C). Note the improved S/I resolution provided by the filtering (C vs. B, E vs. D) and similarity in appearance of (E) vs. (C), suggesting the validity of the simulation.Figure 3 shows the impact of varying $$$\lambda$$$ away from the MMSE-minimizing optimal value.
Table 1 is a summary of MMSE values at optimum values for the three slice profiles for two different patient studies.
Figure 4 shows results from another subject, illustrating subtle but noticeable improved S/I sharpness for rCos (C) vs. measured rect (B) and Gaussian (D) for the same slice thickness. (E) was formed using the same data set as (C) but with $$$\lambda=0.017$$$ (smaller than the MMSE optimum $$$\lambda=0.040$$$), providing improved sharpness as preferred by a collaborating uroradiologist. (F) shows the sagittal reformat formed from experimental axial images acquired with the 3 mm thick rect pulse with 1 mm increment, showing similar overall quality with E.
Discussion
Providing a simulation framework for examining slice excitation profile choice allows rapid evaluation of a range of slice profiles. In this preliminary work rCos demonstrated the ability to provide reduced MMSE vs. Gaussian and measured rect responses for equivalent slice thickness. Further work remains to investigate a larger range of candidate profiles and translate any gains anticipated into actual experimental acquisition. While MMSE is a convenient metric to use for similarity, as shown in the example in Figure 4, it may not be the best proxy for radiologist preference5.Conclusion
A simulation framework for investigating the impact of slice profile selection on the final reconstructed output from an intentionally-overlapped-slices acquisition has been developed. Initial results are visually similar when given similar conditions. Future work includes identifying promising novel slice profiles and testing (through new physical acquisitions) their effectiveness.Acknowledgements
No acknowledgement found.References
- Setsompop K, Fan Q, Stockmann J, Bilgic B, Huang S, Cauley SF, Nummenmaa A, Wang F, Rathi Y, Witzel T, Wald LL, "High-resolution in vivo diffusion imaging of the human brain with generalized slice dithered enhanced resolution: simultaneous multislice (gSlider-SMS)."Magn Reson Med 79:141-151 (2018).
- Okanovic M, Hillig B, Breuer F, Jakob P, Blaimer M, "Time-of-flight MR-angiography with a helical trajectory and slice-super-resolution reconstruction." Magn Reson Med 80:1812-1823 (2018).
- Kargar S, Borisch EA, Froemming AT, Grimm RC, Kawashima A, King BF, Stinson EG, Riederer SJ, "Use of kZ-space for high through-plane resolution in multi-slice MRI: application to prostate." Magn Reson Med 81:3691-3704 (2019).
- Stinson EG, Kargar S, Grimm RC, Riederer SJ. On the selection of slice profile for through-plane resolution in multi-slice MRI imaging. in 27th Ann Mtg, ISMRM. 2019. Montreal Canada.
- Mason A, Rious J, Clarke SE, Costa A, Schmidt M, Keough V, Huynh T, Beyea S, "Comparison of objective image quality metrics to expert radiologists's scoring of diagnostic quality of MR images." IEEE Trans Med Img 39:1064-1072 (2020).
Figures
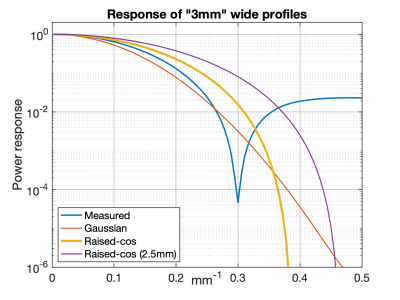
Power response plots of excitation profiles.
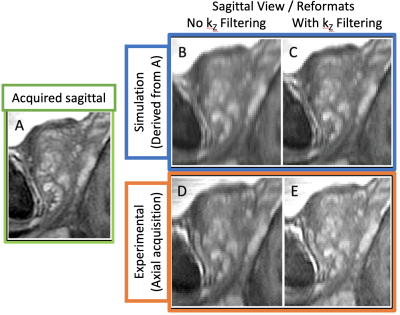
Example native acquired sagittal image (A), simulated acquired signal (B, based on A), and reconstructed signal (C, based on B). Separate native axial acquisition's sagittal reformat (D; averaged to match through-plane thickness of A-C) and as reconstructed (E, based on D). While acquisition planes are not identical, and patient movement is also present, similar SI (up-down as presented) resolution can be appreciated between the reconstructed/refomatted measurement (E) and simulation (C).
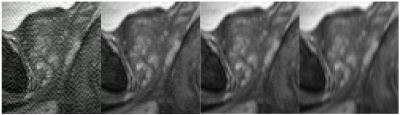
The impact of lambda on reconstruction output. Shown (L-R) at 0.01, 0.5, 1.0, and 5.0⨉ the optimal (0.04, as determined by MMSE) value for a given slice profile and added noise level.
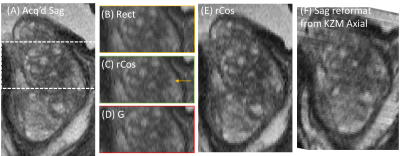
(A) T2SE image of prostate acquired in sagittal orientation. Insets from highlighted region (A) reconstructed using KZM reconstruction of simulated axial sampling are shown for assumed 3mm FWHM rect (B), rCos (C), and Gaussian (D) slice profiles. (C) is sharpest. (E): sagittal reformat similar to (C) but KZM-reconstructed using λ=0.017 (vs. 0.040) giving improved sharpness. (F): sagittal reformat of actual KZM reconstruction from 3mm slices using rect profile.
DOI: https://doi.org/10.58530/2022/1858