1841
Diffeomorphic Image Registration for CINE Cardio MR images using deep learning1Friedrich-Alexander University Erlangen-Nuernberg, Erlangen, Germany, 2Siemens-Healthineers, Erlangen, Germany
Synopsis
Diagnostic applications often require the estimation of organ motion. Image registration enables motion estimation by computing deformation fields for an image pair. In this work, voxelmorph, a framework for deep learning-based diffeomorphic image registration is used to register CINE cardiac MR images in four-chamber view. Additionally, the framework is extended to a one-to-many registration to also utilize temporal information within a time-resolved MR scan. Registration performance as well as the performance of a valve tracking application using this approach are evaluated. The results are comparable to a state-of-the-art registration method, while noticeably reducing the computation time.
Introduction
Motion estimation is an important task for a variety of postprocessing and diagnostic applications1,2 in the medical field. Diffeomorphic image registration solves this task by computing invertible deformation fields for a given image pair.Conventional state-of-the-art approaches solve an optimization problem per image pair3, leading to long computation times, that can be reduced by using a trained neural network for image registration.
Several approaches have been recently proposed for deep learning-based image registration4,5. In this work, the voxelmorph framework is utilized6 to register CINE images. Since voxelmorph does not consider time-resolved data, the method is extended to perform one-to-many registration.
The methods are compared to a state-of-the-art classical registration algorithm7, labeled as “MrFtk” in the following. To demonstrate the applicability of the framework, we integrated and evaluated the framework in a valve tracking application8.
Materials and Methods
Data: The proposed method was trained and tested on CINE scans in four-chamber view. The training data consisted of 1498 scans taken from the UK Biobank data set9 and 40 scans from the Cardiac Atlas Project landmark detection challenge dataset (CAP)10. The remaining 40 scans from the CAP dataset were split into 10 for validation and 30 for testing. For all scans, the intensities above the 95th percentile were clipped and the intensity values were normalized to $$$[0, 1]$$$. Additionally, the scans were transformed to a fixed size of $$$256 \times 256$$$. All scans have a spatial resolution between $$$0.70 mm^2$$$ and $$$2.30 mm^2$$$.Network (Figure 1): The voxelmorph framework computes a deformation field and a moved image from an input image pair. It consists of a 2-D Unet11, scaling and squaring layers and a spatial transformer layer. The approach uses a velocity field representation to ensure diffeomorphic deformations, which is directly computed using the Unet. The deformation field is derived by integrating the velocity field using the scaling and squaring layers. The spatial transformer layer is used to compute a moved image for loss computation.
The one-to-many extension computes $$$n$$$ deformation fields from a CINE series and a reference timeframe being the first frame of the series. The Unet for this approach uses two separate 3-D convolutions in temporal and spatial direction. The rest of the architecture is identical to the architecture described above.
Training: The network loss is a combination of the mean squared error of the moved and the fixed image and a diffusion regularizer6. For the one-to-many extension a temporal smoothness constraint is added, that punishes differing directions and magnitudes of displacement for the same pixel in neighboring timeframes.
Evaluation: Registration performance is evaluated using a landmark distance metric enabled by the ground truth annotations for the mitral valve annulus landmarks of the CAP dataset. The landmark distance error corresponds to the Euclidean distance of the ground truth and registered landmarks. Per timeseries, each timeframe is registered to the first timeframe of the series and the landmark distance error is computed. The results for the evaluation metric are compared to the results obtained by MrFtk. Additionally, the approach is integrated into an existing valve tracking application. Registration is used to propagate the estimated landmarks from the first timeframe throughout the entire timeseries providing an estimate of the mitral valve position in the entire scan, see Figure 4. The propagated landmarks are compared with the ground truth annotations using atrioventricular plane displacement (AVPD), atrioventricular plane velocity (AVPV), annulus diameter (AD) and mitral annular plane systolic excursion (MAPSE) as evaluation metrices.
Results
The results for the registration performance are displayed in Figure 2 a) and b). All methods achieve an average landmark distance error of under $$$1.4 \pm 0.93 mm$$$. The average landmark distance error of $$$1.2 \pm 0.7 mm$$$ achieved by the one-to-many extension does not differ noticeably from the average error of $$$1.2 \pm 0.9 mm$$$ achieved by the classical method. Figure 2 c) shows runtime results for all evaluated methods. The deep-learning-based registration requires up to only $$$75 ms$$$ per scan whereas the comparison method requires $$$10 s$$$ per scan at best, due to the lack of a GPU-implementation. Registration results for an image pair example are shown in Figure 3. Figure 5 a-d) shows the valve tracking results with voxelmorph integration compared to the ground truth annotations of the mitral valve. The average error for all metrices is listed in Figure 5 e).Discussion and Conclusion
The landmark distance error is the highest between the first timeframe (diastolic phase) and timeframes from the interval $$$[8, 16]$$$ (systolic phase), see Figure 2.b). In this case the difficulty of the registration task increases due to the differences between the image pairs. Using additional temporal information within the one-to-many registration decreases this landmark distance error. The corresponding registration performance shows no noticeable difference to the comparison method.When integrated into a valve tracking application, the method performs with error values of under $$$2 mm$$$ for AVPD, AD and MAPSE and an average error value of under $$$0.5 m/s$$$ for AVPV.
Deep-learning-based image registration is comparable to a state-of-the-art approach, while noticeably lowering the computation time, especially when using additional temporal information in a one-to-many registration setting.
Acknowledgements
No acknowledgement found.References
1. Ciprian Catana. Motion correction options in pet/mri. Seminars in Nuclear Medicine, 45(3):212–223, 2015. Clinical PET/MR Imaging (Part I)
2. Seung Su Yoon, Elisabeth Hoppe, Michaela Schmidt, Christoph Forman, Teodora Chitiboi, Puneet Sharma, Christoph Tillmanns, Andreas Maier, and Jens Wetzl. A robust deep-learning-based automated cardiac resting phase detection: Validation in a prospective study, 2020. Presented at International Society for Magnetic Resonance in Medicine (ISMRM) 28th Annual Meeting & Exhibition, Sydney.
3. John Ashburner. A fast diffeomorphic image registration algorithm. NeuroImage, 38(1):95–113, 2007.
4. Marc-Michel Roh´e, Manasi Datar, Tobias Heimann, Maxime Sermesant, and Xavier Pennec. Svf-net: Learning deformable image registration using shape matching. In Medical Image Computing and Computer Assisted Intervention - MICCAI 2017, pages 266–274, Cham, 2017. Springer International Publishing.
5. Sahar Ahmad, Jingfan Fan, Pei Dong, Xiaohuan Cao, Pew-Thian Yap, and Dinggang Shen. Deep learning deformation initialization for rapid groupwise registration of inhomogeneous image populations. Frontiers in Neuroinformatics, 13:34, 2019.
6. Adrian V. Dalca, Guha Balakrishnan, John Guttag, and Mert R. Sabuncu. Unsupervised learning for fast probabilistic diffeomorphic registration. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 729–738. Springer, 2018.
7. Christophe Chefd’Hotel, Gerardo Hermosillo, and Olivier Faugeras. Flows of diffeomorphisms for multimodal image registration. In Proceedings IEEE International Symposium on Biomedical Imaging, pages 753–756. IEEE, 2002.
8. Maria Monzon, Seung Su Yoon, Carola Fischer, Jens Wetzl, Daniel Giese, Andreas Maier. Fully automatic extraction of mitral-valve annulus motion parameters on long axis CINE CMR using deep learning, 2021.
Presented at International Society for Magnetic Resonance in Medicine (ISMRM) 29th Annual Meeting & Exhibition.
9. Cathie Sudlow, John Gallacher, Naomi Allen, Valerie Beral, Paul Burton, John Danesh, Paul Downey, Paul Elliott, Jane Green, Martin Landray, Bette Liu, Paul Matthews, Giok Ong, Jill Pell, Alan Silman, Alan Young, Tim Sprosen, Tim Peakman & Rory Collins (2015). UK biobank: an open access resource for identifying the causes of a wide range of complex diseases of middle and old age. PLoS medicine, 12(3), e1001779.
10. Carissa G. Fonseca, Michael Backhaus, David A. Bluemke, Randall D. Britten, Jae Do Chung, Brett R. Cowan, Ivo D. Dinov, J. Paul Finn, Peter J. Hunter, Alan H. Kadish, Daniel C. Lee, Joao A. C. Lima, Pau Medrano-Gracia, Kalyanam Shivkumar, Avan Suinesiaputra, Wenchao Tao, and Alistair A. Young. The Cardiac Atlas Projectan imaging database for computational modeling and statistical atlases of the heart. Bioinformatics, 27(16):2288–2295, 2011.
11. Olaf Ronneberger, Philipp Fischer, and Thomas Brox. U-net: Convolutional networks for biomedical image segmentation. CoRR, 2015.
Figures

Figure 1: Architectures of the framework used for the one-to-one and one-to-many registration. Subplot a) shows the standard voxelmorph architecture consisting of a 2-D Unet, scaling and squaring layers and a spatial transformer layer. Subplot b) shows the architecture for the one-to-many extension consisting of a 3-D Unet, scaling and squaring layers and a spatial transformer.

Figure 2: Registration performance for the standard voxelmorph method, the one-to-many extension and MrFtk. Subplot a) shows a table with the mean landmark distance error and corresponding standard deviation for the first and second mitral valve annulus landmark as well as the average error for both landmarks. Subplot b) shows a boxplot visualizing the landmark distance error for specific time frame intervals. The orange lines denote the median error values, and the triangles represent the mean error value. Subplot c) shows computation times for all evaluated methods.
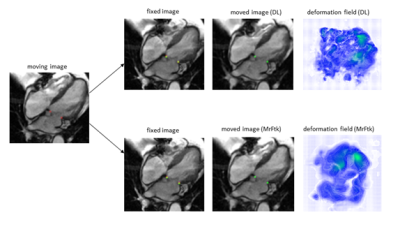
Figure 3: Registration results for the deep-learning-based method and MrFtk. The moving, fixed and moved image are displayed for both registration methods. The ground truth landmarks for the mitral valve insertion points (red) are displayed for the moving and the fixed image. Additionally, the propagated landmarks computed by the proposed framework (green) are displayed for fixed and the moved image. For better visualization, the moving, fixed and moved images as well as the deformation fields are cropped.
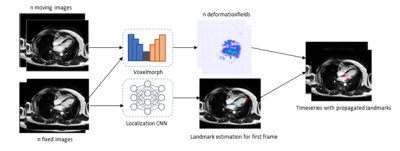
Figure 4: A figure showing the integration of the registration approach into a valve tracking application. Deep-learning-based registration is used to compute deformation fields for a CINE scan. A localization CNN is used to estimate the landmarks of the mitral valve insertion points for the first timeframe. These estimated landmarks are then propagated through the timeseries by spatial transformation with the computed deformation fields.
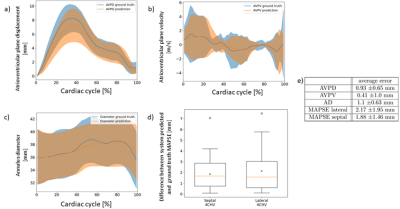
Figure 5: A figure showing the results for the valve-tracking application using the proposed one-to-many registration approach. Subplot a-c) shows the atrioventricular plane displacement, velocity and the annulus diameter, respectively. Subplot d) shows the mitral annular plane systolic excursion error. Subplot e) additionally shows the average error for all metrics. All these metrices are shown for the propagated and the ground truth landmarks of the CAP test dataset.