Introduction

Despite achieving excellent image quality, adopting DL models for MR reconstructions in clinical routine is a concern because of its black-box nature. In such cases, UQ has the potential to provide feedback where the results provided by DL cannot necessarily be trusted.
UQ involves learning a posterior distribution, which is a hard problem in dynamic MR reconstruction because it deals with high-dimensional (space and time) data. Uncertainties can primarily stem from i) the inherent noise present in the output, called the aleatoric uncertainty, and ii) the uncertainties in model parameters, called the epistemic uncertainty [1]. Previous work demonstrated the usage of MCMC dropout with aleatoric loss terms to characterize uncertainty in CINE MRI reconstruction [2]. However, to the best of our knowledge, previous works only considered the computationally less demanding Cartesian single-coil acquisition case. Here, we address the problem of uncertainty quantification for a 2D radial multi-coil cine MR reconstruction problem. Further, we exploit the benefits of ST networks [3,4] at a high-dimensional setting.

Methods

Our goal is to obtain the unknown MRI image $$$\mathbf{x} \in \mathbb{C}^{N_{x} \cdot N_{y}\cdot N_{t} }$$$ from the following ill-posed problem
$$\mathbf{y}_{I} = \mathbf{A}_{I}\mathbf{x} + \mathbf{e} \tag{1},$$
where the operator $$$\mathbf{A}_{I}$$$ contains the radial k-space trajectories and the multi-coil sensitivity maps information. The measured undersampled k-space data is denoted by $$$\mathbf{{y}_{I}}$$$ and is corrupted by random Gaussian noise $$$\mathbf{e}$$$.

End-to-end network: It incorporates acquisition information into the reconstruction process by a three steps training procedure [3] illustrated in Fig. 1 (bottom). The final data-consistent solution $$$\mathbf{x}_{\mathrm{CG}}$$$ is obtained by applying a conjugate gradient algorithm to minimize the problem below, where the network output $$$\mathbf{x}_{\mathrm{CNN}}$$$ serves as a prior.
$$\mathbf{x}_{\mathrm{CG}}:= \underset{\mathbf{x}}{\displaystyle{\arg \min}} \; ||\mathbf{W}^{\frac{1}{2}}(\mathbf{A}_{I}\mathbf{x}-\mathbf{y}_{I})||_{2}^{2}+\lambda||\mathbf{x}-\mathbf{x}_{\mathrm{CNN}}||_{2}^{2} \tag{2}.$$
Here, $$$ \mathbf{W} $$$ is the density compensation matrix.

Spatio-temporal network: A key element of our work is to adopt an ST-Unet (referred here as XTYT-Unet) that takes inputs along the ST perspective. In [4], the authors found that it had the best performance among all 2D-networks and performed comparably well as a 3D-UNet [5], but with a reduced computationally complexity.

Uncertainty quantification: The abbreviations E, C, and K describing the architecture of $$$u_{\theta}$$$ is explained in Fig. 1 (top). Dropout layers with a dropout rate $$$p$$$ are applied before every convolutional block. The following loss function is minimized during training [1,6]:
$$\mathcal{L}(\boldsymbol{\theta})=-\frac{1}{D}\sum_{d=1}^D (\frac{1}{2 (\boldsymbol{\sigma}^{(d)})^2}||\mathbf{x}_{f}^{(d)}-\mathbf{x}_{\scriptscriptstyle{CG}}^{(d)}||_{2}^{2}+\frac{1}{2}\log((\boldsymbol{\sigma}^{(d)})^2)+\frac{1-p}{2D}||\boldsymbol{\theta}||_{2}^{2} \tag{3}.$$
Here, $$$D$$$ is the total pixel number, $$$\sigma$$$ is the aleatoric uncertainty, $$$x_{f}$$$ is the ground truth, and $$$ \theta $$$ denotes network parameters.
The total uncertainty is estimated as the square root of the predictive variance using $$$S$$$ samples-
$$\mathrm{Var}(\mathbf{x}_{\mathrm{CG}})\approx \underbrace{\frac{1}{S}\sum_{s=1}^S (\mathbf{x}_{\mathrm{CG}}^{(s)})^2-(\frac{1}{S}\sum_{s=1}^S \mathbf{x}_{\mathrm{CG}}^{(s)})^2}_{\text{epistemic}}+\underbrace{\frac{1}{S}\sum_{s=1}^S(\boldsymbol{\sigma}^{(s)})^2}_{\text{aleatoric}} \tag{4},$$
where the first two terms correspond to the epistemic uncertainty and the last one to the aleatoric uncertainty.

Dataset and evaluation: Our study uses a dataset of 216 complex-valued cine MRI images with dimensions 320x320x30 (2D space + time dimension) split into 144/36/36 images for training, validation, and testing respectively [3]. The reconstruction quality for the test-set is quantified using NRMSE, PSNR, and SSIM [7].

Result

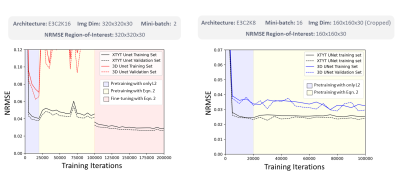
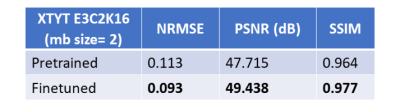
Fig. 2 illustrates the NRMSE trend of XTYT and 3D-Unets during different training phases. The trend for 3D-Unet E3C2K16, trained with a mini-batch size of 2 (mb=2), fails to converge during pretraining. However, when the training images are cropped to 160x160x30, and a lower number of filters in the network are used to be able to fit an mb=16 in the memory, the 3D-Unet E3C2K8 converges. Cropped image size of 160x160x30, however, cannot be used for finetuning because the forward operator requires the entire image whose k-space data is sampled. The training and validation loss of XTYT-Unet E3C2K16 declines further with finetuning after pretraining. Fig. 3 shows that finetuning enhances the RMSE, PSNR, and SSIM values of a pretrained XTYT-Unet E3C2K16. A visual inspection (Fig. 4) of an example slice illustrates the decrease in error and uncertainties for the same finetuned network.

Discussion

There is a good possibility that mb=2 is not sufficient to capture the data uncertainty $$$\sigma$$$ in the output for the 3D-Unet E3C2K16. Hence, its loss fails to converge. This hypothesis is evidenced by the convergence of 3D-Unet E3C2K8 when the mini-batch size is increased to 16. By comparison, the XTYT-Unet E3C2K16 allows for more effective $$$\sigma$$$ learning since slices in this perspective appear to be similar and simpler in structure, holding the observation of [4].
Finally, Fig. 3 and Fig. 4 suggest that including the forward model in the finetuning stage not only reduces the estimation error but also helps decrease the overall uncertainty. The reduction in epistemic uncertainty can be attributed to the fact that the forward model incorporates useful knowledge about the reconstruction process, while aleatoric uncertainty decreases because of less statistical noise in the network output due to improved modeling. Regions of high uncertainty correlate with the error and could be useful input parameters for further diagnosis or even automatic segmentation.

Conclusion

Here, we presented a network that allows for efficient UQ even for a high-dimensional image reconstruction problem such as in non-Cartesian multi-coil CINE MRI. Furthermore, experimental results favor the inclusion of the forward model in the reconstruction process as it decreases the estimation error as well as the uncertainty.

Acknowledgements

We gratefully acknowledge funding from the German Research Foundation (GRK2260, BIOQIC)