1839
Accelerating multi-contrast multidimensional motion-corrected non-Cartesian iterative reconstructions with the Toeplitz approach
Andrew Phair1, Gastao Cruz1, René Botnar1, and Claudia Prieto1
1School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom
1School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom
Synopsis
Iterative reconstructions for multi-contrast multidimensional non-Cartesian MRI can require considerable computation time, with a large fraction dedicated to non-uniform fast Fourier transforms (NUFFTs). The Toeplitz approach has been previously shown to allow NUFFT operations to be replaced by computationally efficient fast Fourier transforms (FFTs) without loss of accuracy. Herein, we combine this approach with a 3D multi-contrast low-rank cardiac-motion-corrected radial reconstruction with low-rank patch-based regularisation to achieve a ~13.3-fold computational speed-up.
Introduction
Many reconstruction methods for non-Cartesian k-space data acquisitions utilise iterative schemes requiring a multiplication by $$$E^{\ast}E$$$ each iteration, where $$$E$$$ is a forward operator which models the k-space acquisition. Such multiplications can be computationally expensive given the requirement for numerous applications of non-uniform fast Fourier transforms (NUFFTs), especially in the case of multi-contrast multidimensional imaging methods where long reconstruction times can remain a hindrance to clinical adoption. The Toeplitz approach1-5 has been demonstrated to provide significant acceleration by replacing NUFFT operations with far-more efficient FFT operations whilst achieving identical images. Herein, we combine the approach with a 3D multi-contrast low-rank cardiac-motion-corrected radial reconstruction, where it is seen to accelerate the total reconstruction ~13.3-fold.Theory
Consider a 2D imaging sequence with an arbitrary non-Cartesian k-space sampling pattern, noting that the following formalism can be generalised to 3D.For $$$N$$$ image pixels and $$$K$$$ k-space samples, let the forward operator be $$$E=DFB$$$, where $$$B\in\mathbb{C}^{N{\times}N}$$$ is an image-space operator (e.g. coil sensitivity multiplication), $$$F\in\mathbb{C}^{K{\times}N}$$$ is the non-uniform Fourier transform and $$$D\in\mathbb{C}^{K{\times}K}$$$ is a diagonal matrix which applies a multiplication in k-space (e.g. density compensation). In an iterative reconstruction an image-space object $$$\boldsymbol{\rho}\in\mathbb{C}^{N{\times}1}$$$ is multiplied by$$E^{\ast}E=B^{\ast}F^{\ast}D^{\ast}DFB$$where $$$\ast$$$ denotes the conjugate transpose, $$$F^\ast$$$ is the inverse non-uniform Fourier transform and $$$D^\ast=\bar{D}$$$, since D is diagonal. For convenience, we define$$\mathbf{v}=B\boldsymbol{\rho}$$and$$\mathbf{g}=F^{\ast}D^{\ast}DF\mathbf{v}.$$We now seek to represent these discrete equations using continuous functions. Letting the Cartesian image-space grid be$$C\left(x,y\right)=\sum_{i}\sum_{i}\delta\left(x-x_i,y-y_j\right),$$and the arbitrary k-space sampling pattern be$$R\left(k_x,k_y\right)=\sum_{m}\delta\left(k_x-\left(k_x\right)_m,k_y-\left(k_y\right)_m\right),$$where $$$\delta$$$ is the Dirac delta function, we have$$g\left(x,y\right)=C\left(x,y\right)\mathcal{F}^{-1}\left\{\bar{d}\left(k_x,k_y\right)d\left(k_x,k_y\right)R\left(k_x,k_y\right)\mathcal{F}\left\{v\left(x,y\right)C\left(x,y\right)\right\}\right\}$$where $$$\mathcal{F}$$$ is the continuous Fourier transform and the functions $$$g\left(x,y\right)$$$, $$$d\left(k_x,k_y\right)$$$ and $$$v\left(x,y\right)$$$ take the values in $$$\mathbf{g}$$$, $$$D$$$ and $$$\mathbf{v}$$$ at the grid or sample locations and are defined arbitrarily elsewhere. By the convolution theorem, the k-space multiplication in this equation may be replaced by an image-space convolution, yielding $$g\left(x,y\right)=C\left(x,y\right)\left(p\left(x,y\right){\otimes}\left[v\left(x,y\right)C\left(x,y\right)\right]\right),$$where $$$\otimes$$$ denotes the convolution and$$p\left(x,y\right)=\mathcal{F}^{-1}\left\{\bar{d}\left(k_x,k_y\right)d\left(k_x,k_y\right)R\left(k_x,k_y\right)\right\},$$which we note acts as a point-spread function. Since the Cartesian grid $$$C\left(x,y\right)$$$ multiplies one side of the convolution and the output of the convolution, we may return to the discrete equation$$\mathbf{g}=A^{-1}\left(P{\otimes}A\left(v\right)\right)=A^{-1}\left(P{\otimes}A\left(B\boldsymbol{\rho}\right)\right),$$where $$$P\in\mathbb{C}^{2N_x{\times}2N_y}$$$ is the point-spread function sampled on a grid which extends to twice the image width in each direction and $$$A$$$ rearranges $$$N$$$-long image-vectors to $$$N_x{\times}N_y$$$ matrices. The multiplication by $$$E^{\ast}E$$$ may thus be expressed as$$E^{\ast}E\boldsymbol{\rho}=B^{\ast}A^{-1}\left(P{\otimes}A\left(B\boldsymbol{\rho}\right)\right).$$Finally, we apply the discrete convolution theorem to utilise a computationally efficient multiplication in Cartesian k-space, which may be accessed via FFTs, yielding$$E^{\ast}E\boldsymbol{\rho}=B^{\ast}\mathrm{IFFT}\left\{\mathrm{FFT}\left\{P\right\}{\circ}\mathrm{FFT}\left\{B\boldsymbol{\rho}\right\}\right\},$$where $$$\circ$$$ denotes the Hadamard (elementwise) product.
For a given k-space sampling pattern and operator $$$D$$$, the point-spread function in k-space, $$$\mathrm{FFT}\left\{P\right\}$$$, may be pre-calculated using the NUFFT once and saved. Multiplications by $$$E^{\ast}E$$$ occurring in each iteration of a reconstruction algorithm may then be implemented in accordance with this final equation.
Experiments
The Toeplitz approach was applied to the reconstruction of 3D multi-contrast cardiac-motion-corrected whole-heart images from a 3D free-running golden-angle radial k-space acquisition with interleaved IR and $$$T_2$$$-prep pulses6 at a reference cardiac phase. The reconstruction was performed iteratively via an ADMM7 scheme, which alternated between HD-PROST8 denoising and enforcement of the data consistency constraint $$$\|E\boldsymbol{\rho}-W\mathbf{k}\|_2^2$$$ via conjugate gradient (CG) iteration. Here, $$$E$$$ is the forward operator of a dictionary-based low-rank motion-corrected reconstruction (LRMC)9 given as $$$E=\sum_{q}WU_rA_qF_qSM_q$$$, where $$$q$$$ represents cardiac phases, $$$M_q$$$ is a motion field, $$$S$$$ contains coil sensitivity maps, $$$A_qF_q$$$ applies the Fourier transform for the $$$q$$$th phase, and $$$W$$$ and $$$U_r$$$ are density-compensation and low-rank dictionary-compression weights which multiply k-space samples. Since different spokes are acquired at each phase, and different weights in $$$U_r$$$ are applied for the $$$r$$$ contrast images, $$$r^2$$$ point-spread functions must be calculated for each phase.Reconstructions using the Toeplitz approach were compared with those using NUFFTs10. The total number of 3D Fourier transforms required (forwards and inverse) was 17,280, for the reconstruction parameters: 10 cardiac phases, 8 coils, $$$r$$$=3 SVD-compressed contrasts and 3 ADMM iterations each involving 4 CG iterations. Each transform was between a 100$$$\times$$$100$$$\times$$$100 image-space object and a ~5850$$$\times$$$200 radial k-space.
The resultant multi-contrast 3D images are presented in Figure 2 and are identical to within the order of machine epsilon.
The computational times for the two methods are presented in Figure 3. For both methods, $$$E^{\ast}\left(W\mathbf{k}\right)$$$ is pre-calculated for use in each ADMM iteration. The results show that a multiplication by $$$E^{\ast}E$$$ using the Toeplitz approach was ~150 times faster than using NUFFTs, while the combined pre-calculation and iterative reconstruction was ~13.3 times faster.
Discussion
Significant computational acceleration was achieved for the 3D motion-corrected multi-contrast iterative reconstruction scheme from a free-running 3D scan. The Toeplitz approach is particularly well-suited to this scheme given the large data sizes and number of NUFFT operations required. We note that the NUFFT implementation employed here may not be optimal, and in particular GPU-based implementations would be expected to be more efficient.The calculation of the point-spread function (~26% of total time in the example case) is in general not required for every reconstruction. In scenarios where the same k-space trajectory and operator $$$D$$$ apply, a single point-spread function can be calculated and applied for every scan.
Conclusion
The Toeplitz approach was utilised to replace NUFFT operations with FFT operations for a 3D multi-contrast cardiac-motion-corrected radial reconstruction, achieving a ~13.3-fold acceleration of the reconstruction time.Acknowledgements
This work was supported by EPSRC (EP/P001009, EP/P032311/1, EP/P007619/1) and Wellcome EPSRC Centre for Medical Engineering (NS/ A000049/1).References
1. Liu, C., Moseley, M. E., & Bammer, R. (2005, May). Fast SENSE reconstruction using linear system transfer function. In Proc. Intl. Soc. Mag. Res. Med (p. 689).2. Fessler, J. A., & Noll, D. C. (2007). Iterative reconstruction methods for non-Cartesian MRI. In Proc. ISMRM Workshop on Non-Cartesian MRI (Vol. 29, pp. 222-229).
3. Ahmad, R., Austin, C. D., & Potter, L. C. (2011, May). Toeplitz embedding for fast iterative regularized imaging. In Algorithms for Synthetic Aperture Radar Imagery XVIII (Vol. 8051, p. 80510E). International Society for Optics and Photonics.
4. Mani, M., Jacob, M., Magnotta, V., & Zhong, J. (2015). Fast iterative algorithm for the reconstruction of multishot non‐cartesian diffusion data. Magnetic resonance in medicine, 74(4), 1086-1094.
5. Baron, C. A., Dwork, N., Pauly, J. M., & Nishimura, D. G. (2018). Rapid compressed sensing reconstruction of 3D non‐Cartesian MRI. Magnetic resonance in medicine, 79(5), 2685-2692.
6. Qi, H., Bustin, A., Cruz, G., Jaubert, O., Chen, H., Botnar, R. M., & Prieto, C. (2019). Free-running simultaneous myocardial T1/T2 mapping and cine imaging with 3D whole-heart coverage and isotropic spatial resolution. Magnetic resonance imaging, 63, 159-169.
7. Boyd, S., Parikh, N., & Chu, E. (2011). Distributed optimization and statistical learning via the alternating direction method of multipliers. Now Publishers Inc.
8. Bustin, A., Lima da Cruz, G., Jaubert, O., Lopez, K., Botnar, R. M., & Prieto, C. (2019). High‐dimensionality undersampled patch‐based reconstruction (HD‐PROST) for accelerated multi‐contrast MRI. Magnetic resonance in medicine, 81(6), 3705-3719.
9. Cruz, G., Qi, H., Jaubert, O., Kuestner, T., Schneider, T., Botnar, R. M., & Prieto, C. (2021). Generalized low‐rank nonrigid motion‐corrected reconstruction for MR fingerprinting. Magnetic Resonance in Medicine.
10. Greengard, L., & Lee, J. Y. (2004). Accelerating the nonuniform fast Fourier transform. SIAM review, 46(3), 443-454
Figures

Fig 1. Diagrams of the (a) NUFFT-based and (b) Toeplitz approach to applying $$$F^{\ast}D^{\ast}DF$$$ to an image-space object. For the Toeplitz approach the input image is zero-padded to twice the image size in each direction, and the output image is cropped to the image size to give the same result as the NUFFT-based implementation.
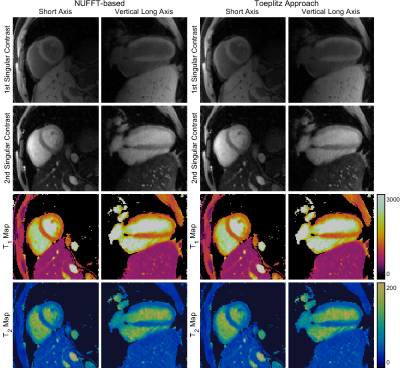
Fig 2. 2D slices of 3D singular-contrast images produced by NUFFT-based iterations (left) and the Toeplitz approach (right), shown in the short axis and vertical long axis orientation for the 1st and 2nd singular contrasts, and the $$$T_1$$$ and $$$T_2$$$ maps obtained via voxel-wise dictionary matching. The images are identical to within the order of machine epsilon.
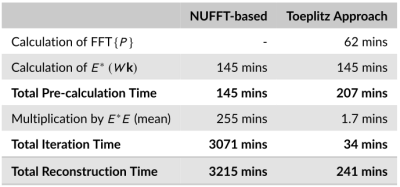
Fig 3. Comparison of the computation
times for the NUFFT-based approach and the Toeplitz approach
DOI: https://doi.org/10.58530/2022/1839