1819
Scan acceleration by oversampling in a 70 mT MRI scanner1MRILab, Institute for Molecular Imaging and Instrumentation (i3M), Spanish National Research Council (CSIC), Valencia, Spain, 2MRILab, Institute for Molecular Imaging and Instrumentation (i3M), Universitat Politècnica de València (UPV), Valencia, Spain, 3Tesoro Imaging SL, Valencia, Spain, 4Physio MRI SL, Valencia, Spain
Synopsis
Here we present accelerated images by PhasE-Constrained Over Sampled (PECOS) MRI in our home-made Halbach MRI scanner (70 mT). We show projection images of a phantom obtained in our “PhysioMRI” scanner (Fig. 1(a)), a home-made scanner designed for musculoskeletal imaging at low field strengths. We use cartesian turbo spin echo (TSE) sequence to sample the k-space. Image reconstructions are performed by phase conjugate reconstruction and by PECOS.
Introduction
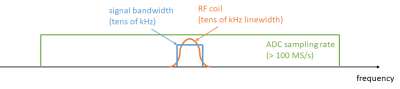
Data oversampling (OS) along the readout or frequency-encoded direction in MRI is typically used for avoiding aliasing from active spins outside the region of interest or increasing the signal-to-noise ratio (SNR) and dynamic range of the analog-to-digital converters (ADC) outputs [1]. Here we propose an alternative use of the OS data and demonstrate that it can accelerate the total scan time if combined with undersampling along phase-encoded directions.Figure 1 illustrates the spectral distributions of the three elements we will consider in this work. First we have the signal bandwidth, which is determined by the extent of the field of view (FoV) and the encoding gradient strength. Secondly, the ADC samples at a rate which determines the bandwidth where it is sensitive. Lastly, the resonant radio-frequency (RF) detector has a linewidth determined by its quality factor. For low-field systems, where the detector linewidth (10-50 kHz) is on the order or even narrower than the signal bandwidth [2], high oversampling rates (> 100) are feasible with state-of-the-art ADCs (> 100 MS/s). The additional data points constitute noiseless measurements to a good approximation, since any fast noise fluctuation should be efficiently suppressed by the resonant character of the RF coil. This can be used for scan acceleration if the information of missing k-space lines is compensated for with the extra samples and (available) phase information from the sampled object. This can be then reconstructed iteratively with a PhasE-Constrained Kaczmarz algebraic reconstruction technique (PECOS) [3-5].
In this work, we present our “PhysioMRI” scanner, a home-made 72 mT system based on the previous work by Thomas O’Reilly et al. [6], and demonstrate the performance of the aforementioned OS techniques for scan acceleration.
Methods
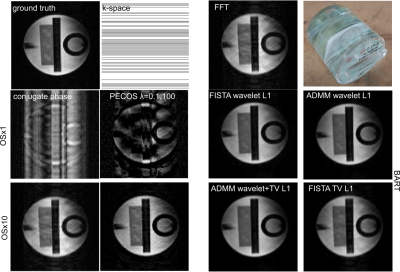
The “PhysioMRI” scanner (Fig. 2(a) and (b)) operates with a Halbach array of 4,575 NdFeB magnets (Fig. 2(c)) of 12x12x12 mm3, providing ~72 mT over a spherical region of 200 mm in diameter with homogeneity of 15,700 ppm. The shimming system (Fig. 2(d)) consists of 1,080 additional magnets of 3x3x3 mm3 that reduce the homogeneity to 3,095 ppm. The scanner is equipped with a gradient system (Fig. 2(e)) capable of reaching strengths > 24 mT/m along any spatial direction, and a TxRx RF solenoid coil (Fig. 2(f)) with 44 turns, 15 cm diameter, 15 cm length and Q = 120, sufficient for pi/2 rotations in 10 microseconds. We control the scanner with MaRCoS [7], a Red Pitaya based system (Fig. 2(g)) controlling a custom gradient driver board [8].To acquire the data below, we use turbo spin-echo (TSE) sequences. We use an RF power of 10 W, pi/2-pulses of 35 µs and refocusing pi-pulses of 70 µs. The phase cycling of the refocusing pulses in the TSE follows a Carr-Purcell-Meiboom-Gill modulation. For the results in Fig. 3, we run two independent scans: one Nyquist limited, the second with OS x10. The ground truth results from an FFT of the Nyquist limited acquisition. We show a 2D slice from each 3D acquisition, with a FoV spanning a bandwidth of 33 kHz. The x10 oversampled acquisition is sampled at 330 kS/s and CIC-filtered at 330 kHz [9]. Our reception coil has a linewidth of ~25 kHz, so oversampling introduces a negligible amount of additional noise.
Results
For the CP, PECOS and BART reconstructions in Fig. 3 we keep the 10 central lines of k-space (10 %) and remove half the readout lines from the rest. Both CP and PECOS show that a x2 phase-undersampled acquisition can be reconstructed, but PECOS shows an overall increase in sharpness and a better discrimination of brightness for different regions. This is a consequence of including the phase information prior. We have also used the Berkeley Advanced Reconstruction Toolbox (BART, [11]) with l1-regularization based on wavelets and/or total variation [12]. The overall performance of PECOS is comparable, if not better, than that of the ADMM and FISTA protocols in BART.Discussion
In this work we show highly readout-oversampled TSE acquisitions of an MRI phantom in a 72 mT custom-built MRI system. Further use of a phase-constrained Kaczmarz algorithm leads to an improved reconstruction for a x2 phase-undersampled k-space where its 10 % center is fully sampled, showing an alternative method to use a phase prior which is independent of wavelet/TV l1-regularizations.Acknowledgements
We acknowledge Thomas O’Reilly and Andrew Webb from LUMC for discussions. This work was supported by the Ministerio de Ciencia e Innovación of Spain through research grant PID2019-111436RBC21. Action co-financed by the European Union through the Programa Operativo del Fondo Europeo de Desarrollo Regional (FEDER) of the Comunitat Valenciana 2014-2020 (IDIFEDER/2018/022).References
[1] Smith, Nadine Barrie, and Andrew Webb, Introduction to Medical Imaging (Cambridge University Press, 2010)
[2] ESMRMB 2021, Abstract S5.O3
[3] Galve, Fernando, Joseba Alonso, José M Algarín, and José M Benlloch, ‘Model-Driven Reconstruction with Phase-Constrained Highly-Oversampled MRI’, arXiv Preprint, 2020, 2007.15674
[4] Gordon, Richard, Robert Bender, and Gabor T. Herman, ‘Algebraic Reconstruction Techniques (ART) for Three-Dimensional Electron Microscopy and X-Ray Photography’, Journal of Theoretical Biology, 29 (1970), 471–81
[5] Elfving, T. et al., Inverse Problems 30, 055007 (2014); Wu, N. and Xiang, H., J. Comp. App. Mat. 372, 112672 (2020).
[6] O’Reilly, Thomas, Wouter M. Teeuwisse, Danny Gans, Kirsten Koolstra, and Andrew G. Webb, ‘In Vivo 3D Brain and Extremity MRI at 50 MT Using a Permanent Magnet Halbach Array’, Magnetic Resonance in Medicine, 2020, mrm.28396
[7] V. Negnevitsky et al. MaRCoS: A high-performance open-source control system for affordable MRI. 116 proceedings ESMRMB, 2021.
[8] https://zeugmatographix.org/ocra/2020/11/27/ocra1-spi-controlled-4-channel-18bit-dac-and-rf-attenutator/
[9] https://www.xilinx.com/support/documentation/ip_documentation/cic_compiler/v4_0/pg140-cic-compiler.pdf
[10] Macovski, Albert, ‘Volumetric NMR Imaging with Time-Varying Gradients’, Magnetic Resonance in Medicine, 2 (1985), 29–40
[11] BART Toolbox for Computational Magnetic Resonance Imaging, DOI: 10.5281/zenodo.592960
[12] Uecker M. et al., Software Toolbox and Programming Library for Compressed Sensing and Parallel Imaging, ISMRM Workshop on Data Sampling and Image Reconstruction, Sedona 2013
Figures