1816
Physics-Informed Deep Learning for Image Distortion Correction from B0-inhomogeneities in Low-Field MRI
David Schote1, Lukas Winter1, Christoph Kolbitsch1, Felix Zimmermann1, Thomas O'Reilly2, Andrew Webb2, Frank Seifert1, and Andreas Kofler1
1Physikalisch-Technische Bundesastalt (PTB), Braunschweig and Berlin, Germany, 2C.J. Gorter Center for High Field MRI, Department of Radiology, Leiden University Medical Center, Leiden, Netherlands
1Physikalisch-Technische Bundesastalt (PTB), Braunschweig and Berlin, Germany, 2C.J. Gorter Center for High Field MRI, Department of Radiology, Leiden University Medical Center, Leiden, Netherlands
Synopsis
A physics-informed deep neural network using a U-Net in combination with a multifrequency interpolation is presented to correct for B0-field image distortions in low-field MRI. Training data is based on 1.5T and 3.0T knee images and realistic measurement-based assumption of SNR and B0-field inhomogeneities from previously constructed Halbach magnets. Significant (p<0.05) improvements are demonstrated applying the suggested methodology to uncorrected images.
Introduction
Low-field MRI has the potential to provide point-of-care diagnostic imaging and improve access to MR technology globally1-4. Currently, affordable open-source low-field MR systems are being assembled, based on permanent magnets in Halbach arrangements5-7. The $$$B_0$$$-homogeneity of these magnets is by orders of magnitudes worse compared to current 1.5T and 3.0T clinical systems and is affected by environmental factors such as temperature drifts. Model-based approaches can be used to correct for $$$B_0$$$-related image distortions, however with an additional burden in computational and signal acquisition time8. Previous work on 3T data demonstrated that off-resonance maps can be estimated by machine learning methods9,10. Consequently, to improve affordable low-field MR design, this work investigates deep learning-based methods for image reconstruction in low-field MRI.Methods
Training dataSufficient quantities of low-field MR data are not currently available for training. For this work, 3T and 1.5T imaging data of the knee11 were modified by deteriorating the $$$B_0$$$-field homogeneity and SNR (Figure-1). The $$$B_0$$$-field of a Halbach-based low-field MR magnet can be sufficiently characterized by a truncated set of spherical harmonics12. Based on this information and the available measured field homogeneity over the FoV5, randomized field variations were estimated. Through forward computation13, the artificially generated off-resonance maps were applied to the initial data by the following relation
$$S(t)\;=\;\int_r\;\rho(r)\;e^{-i\,\Delta\omega_0(r)\,t}e^{-i\,2\pi\,k(t)\,r}\;dr.$$
Relative to the standard deviation of the given k-space data, random normal (Gaussian) noise was added to degrade the SNR to levels typical for in-vivo low-field MRI5. Since only magnitude images were available, the phase signal was simulated by the superposition of randomized sinusoidal functions14.
Network for off-resonance estimation
We used a 2D U-Net to estimate the off-resonance map $$$\Delta\omega_0(r)$$$ from the simulated complex data only. It is constructed with 3 encoding stages, each consisting of 2 convolutional layers with $$$3\times3$$$ convolution kernels. The initial number of 12 filters per convolutional layer is doubled after the intermediate $$$2\times2$$$ max-pooling layers in the encoding path and halved in the decoding path. The neural network is equipped with two input channels for the real and imaginary part of the training data (MR images), and a single output channel for the estimated real-valued field map.
Physics-informed training
First, the network is pretrained based on an L1-loss function between the $$$B_0$$$-field estimate and the ground truth $$$B_0$$$ map (Figure 2). For stabilization of the training process15 and reduction of the required amount of training data16, a physical model, describing the effect of $$$B_0$$$-inhomogeneities was included in the network for additional fine-tuning. To decrease the computational burden in comparison to conjugate phase reconstruction (CPR), multifrequency interpolation (MFI)17 was implemented as the physical model in PyTorch enabling end-to-end training. MFI calculations were performed on a GPU (GeForce RTX 2080 Ti). Note that from the fine-tuning step, we do not expect a substantial improvement in the reconstruction result as there is no regularization imposed on the images at this stage. For the refinement, an L2-foss function between the reconstruction with estimated and ground-truth $$$B_0$$$ map was used.
Results
Figure 3 illustrates the absolute validation error of the field map (Figure 3a) and the reconstructed image (Figure 3b) from pretraining and refinement. The refinement step resulted in a minor drop of the loss function and decreased the variance in the loss function, which indicates a higher degree of stability that is achievable when embedding a physical model. The results from the deep learning-based $$$B_0$$$-field correction applying the MFI reconstruction are shown in Figure-4 and compared to an uncorrected image and a correction based on the known $$$B_0$$$-field. It is visible that in general a higher distortion is expected towards the edges of the FoV. For an improved error assessment of the field-based distortions across all investigated datasets, an OTSU threshold-based image segmentation18 was performed and applied to access the point-wise error of the knee. This distortion difference was compared to the RMS- and SSIM-errors (Figure-5). The segmented object-difference in terms of the median was significantly improved (p<0.05) from 3.783E-2 to 2.388E-2 for the U-Net and 2.297E-2 applying the refined estimation, respectively. The segmented object-difference of the MFI-reconstruction applying the known $$$B_0$$$-field distribution was 1.048E-2. Similar results were observed for the RMSE and SSIM (Figure-5).Discussion and Conclusion
We present a physics-informed deep neural network using a U-Net in combination with an MFI implemented in PyTorch. We showed that image distortion due to $$$B_0$$$-field inhomogeneities can be reduced by such a network on simulated low-field MR images. The quantification of the performance can be further optimized since the poor signal-to-noise ratio led to many outliers in the proposed comparison. So far, the training results are dependent on simplified simulations, and more realistic results might be obtained by Bloch simulations. End-to-end iterative networks for image reconstruction could be applied to further improve the results19. An image-based correction would relax $$$B_0$$$-field homogeneity specifications for magnets and is a potential alternative to the utilization of field probes in the MR system. These measures reduce the complexity and consequently the cost for low-field MR hardware. Future investigations are needed to validate the presented approach with measured in-vivo low-field MR data.Acknowledgements
This work is part of the Metrology for Artificial Intelligence for Medicine (M4AIM) project that is funded by the Federal Ministery for Economic Affairs and Energy (BMWi) in the frame of the QI-Digital initiative.References
- Wald LL, McDaniel PC, Witzel T, Stockmann JP, Cooley CZ. Low‐cost and portable MRI. J Magn Reson Imaging. 2020;52(3):686-696. doi:10.1002/jmri.26942
- Sarracanie M, Salameh N. Low-Field MRI: How Low Can We Go? A Fresh View on an Old Debate. Front Phys. 2020;8:172. doi:10.3389/fphy.2020.00172
- Cooley CZ, McDaniel PC, Stockmann JP, et al. A portable scanner for magnetic resonance imaging of the brain. Nat Biomed Eng. 2021;5(3):229-239. doi:10.1038/s41551-020-00641-5
- O’Reilly T, Teeuwisse WM, Gans D, Koolstra K, Webb AG. In vivo 3D brain and extremity MRI at 50 mT using a permanent magnet Halbach array. Magn Reson Med. 2021;85(1):495-505. doi:10.1002/mrm.28396
- O’Reilly T, Teeuwisse WM, Webb AG. Three-dimensional MRI in a homogenous 27 cm diameter bore Halbach array magnet. Journal of Magnetic Resonance. 2019;307:106578. doi:10.1016/j.jmr.2019.106578
- Winter L. Open Source Imaging. Launching the next stage of the Open Source MR project. June 1, 2021. Accessed November 8, 2021. https://www.opensourceimaging.org/2021/06/01/launching-the-next-stage-of-the-open-source-mr-project/
- Koolstra K, O’Reilly T, Börnert P, Webb A. Image distortion correction for MRI in low field permanent magnet systems with strong B0 inhomogeneity and gradient field nonlinearities. Magn Reson Mater Phy. Published online January 27, 2021. doi:10.1007/s10334-021-00907-2
- Zeng DY, Shaikh J, Holmes S, et al. Deep Residual Network for Off-Resonance Artifact Correction with Application to Pediatric Body Magnetic Resonance Angiography with 3D Cones. Published online 2020:24.
- Haskell MW, Cao AA, Noll DC, Fessler JA. Deep learning field map estimation with model-based image reconstruction for off resonance correction of brain images using a spiral acquisition. 2020.
- Bien N, Rajpurkar P, Ball RL, et al. Deep-learning-assisted diagnosis for knee magnetic resonance imaging: Development and retrospective validation of MRNet. Saria S, ed. PLoS Med. 2018;15(11):e1002699. doi:10.1371/journal.pmed.1002699
- Wenzel K, Alhamwey H, O’Reilly T, Riemann LT, Silemek B, Winter L. B0-Shimming Methodology for Affordable and Compact Low-Field Magnetic Resonance Imaging Magnets. Front Phys. 2021;9:704566. doi:10.3389/fphy.2021.704566
- Jimeno MM, Vaughan JT, Geethanath S. Imr-Framework/OCTOPUS: JOSS. Zenodo; 2021. doi:10.5281/ZENODO.4574444
- Schlemper J, Castro DC, Bai W, et al. Bayesian Deep Learning for Accelerated MR Image Reconstruction. In: Knoll F, Maier A, Rueckert D, eds. Machine Learning for Medical Image Reconstruction. Vol 11074. Lecture Notes in Computer Science. Springer International Publishing; 2018:64-71. doi:10.1007/978-3-030-00129-2_8
- Kofler A, Haltmeier M, Schaeffter T, Kolbitsch C. An end‐to‐end‐trainable iterative network architecture for accelerated radial multi‐coil 2D cine MR image reconstruction. Med Phys. 2021;48(5):2412-2425. doi:10.1002/mp.14809
- Gilton D, Ongie G, Willett R. Neumann Networks for Inverse Problems in Imaging. arXiv:190103707 [cs, stat]. Published online June 3, 2019. Accessed November 9, 2021. http://arxiv.org/abs/1901.03707
- Kofler A, Haltmeier M, Schaeffter T, Kolbitsch C. An end‐to‐end‐trainable iterative network architecture for accelerated radial multi‐coil 2D cine MR image reconstruction. Med Phys. 2021;48(5):2412-2425. doi:10.1002/mp.14809
- Man LC, Pauly JM, Macovski A. Multifrequency interpolation for fast off-resonance correction. Magn Reson Med. 1997;37(5):785-792. doi:10.1002/mrm.1910370523
- Goh TY, Basah SN, Yazid H, Aziz Safar MJ, Ahmad Saad FS. Performance analysis of image thresholding: OTSU technique. Measurement. 2018;114:298-307. doi:10.1016/j.measurement.2017.09.052
- Ravishankar S, Ye JC, Fessler JA. Image Reconstruction: From Sparsity to Data-Adaptive Methods and Machine Learning. Proc IEEE. 2020;108(1):86-109. doi:10.1109/JPROC.2019.2936204
Figures
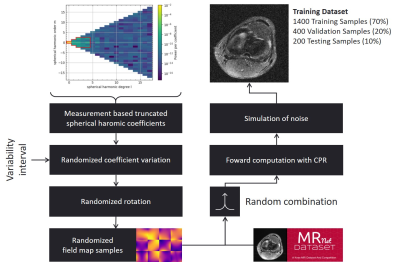
Methodology to generate artificial low-field MRI training
datasets. As a basis for this work, the MRNet dataset has been used and
modified, which consists of 1.5T and 3T MR images of the knee10. This data
was modified to reach SNR levels previously measured on a low-field MR system5.
B0-field variations are based on a truncated spherical
harmonics approach11 and measured B0-field homogeneity of a
low-field MR magnet5.
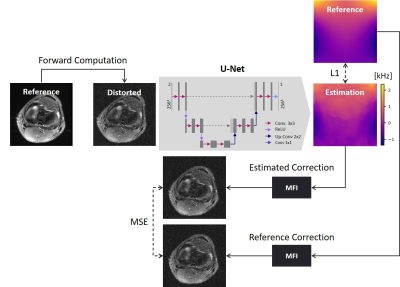
Deep learning
methodology to estimate the B0-field distribution from distorted
image datasets by a U-Net through L1-error and refinement using a multifrequency interpolation through L2-error of the reconstruction.
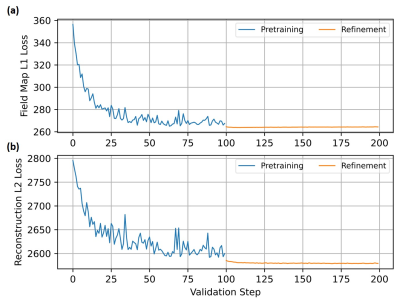
Validation error given as the
(a) L1-error
between the estimated and target field map and (b) L2-error
between the reconstruction with estimated and target field map during pretraining
(blue) and refinement (orange). For the pretraining only the L1-error
and for the refinement the L2-error
was utilized. During the refinement stage a minor decrease
of the loss function, but a decrease of the variance can be noticed, which
indicates a higher degree of stability that is achievable by embedding a
physical model.
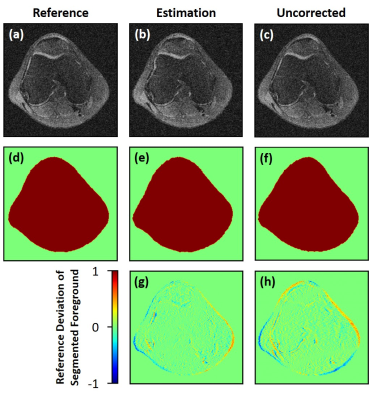
Example of the deep
learning image-based distortion correction of a knee image. (a) MFI
reconstruction including correction from ground truth B0-field reference. (b)
MFI reconstruction using the estimated B0-field map based on the deep learning
approach. (c) Uncorrected distorted knee image. (d-f) OTSU-based knee
segmentation masks for the corresponding images (a-c). The point-wise
error-images of the segmented knee are depicted and compared for (g) the deep learning-based
estimation and (h) the uncorrected image.
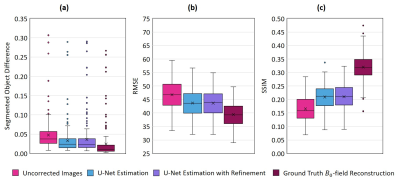
Comparison of relative error in
difference map of segmentation (Fig. 4) in (a), root mean squared error (RMSE)
in (b) and structural similarity index (SSIM) in (c) for off-resonance image
and MFI reconstructions.
The segmented object-difference in terms of the median was significantly
improved (p<0.05) from 3.783E-2 to 2.388E-2 for the U-Net and 2.297E-2
applying the refined estimation, respectively. The segmented object-difference
of the MFI-reconstruction applying the known B0-field
distribution was 1.048E-2.
DOI: https://doi.org/10.58530/2022/1816