1808

Random Matrix Theory reconstruction for T1 quantification on a field-cycling scanner for B0 ranging between 2-200mT

Gregory Lemberskiy^1,2, Vasiliki Mallikourti³, Dmitry S Novikov¹, and Lionel M Broche³
¹Radiology, New York University Grossman School of Medicine, New York, NY, United States, ²Microstructure Imaging INC, New York, NY, United States, ³Aberdeen Biomedical Imaging Centre, University of Aberdeen, Aberdeen, United Kingdom

Synopsis

We showcase high SNR T1 maps over a range of low field strengths on a stroke patient imaged using a field-cycling imaging scanner (FCI), an MR system capable of varying B0 over 2 orders of magnitude. Images from this scanner are denoised using Random Matrix Theory (RMT), leveraging the redundancy over multiple inversion times and field strengths to increase the baseline SNR by 3-fold. Following RMT denoising, we observe the T1 dispersion effect indicating a deviation of R1 frequency dependence from the BPP theory.

Introduction

In recent years, there has been a resurgence of interest in low-field MR systems, which include the commercialization of imaging systems such as the 0.55T Siemens Free.Max and the 65 mT Hyperfine Swoop. It was recently shown¹ that not only are particular applications more cost effective at low-field, but may have clear advantages over high field systems. These advantages include (1) higher $$$T_2$$$/lower $$$T_1$$$ allowing for shorter readouts, (2) lower magnetic susceptibility to enable atypical imaging trajectories and imaging near air/tissue interfaces, particularly around the lungs and abdomen. At even lower field strengths, below $$$<100\,\mathrm{mT}$$$, the observed $$$T_1$$$ deviates from BPP theory^2,3, and $$$T_1$$$ contrast reflects cross-relaxation with nitrogen resonances⁴. This reveals a contrast mechanism, called $$$T_1$$$-dispersion, which is unique to low field systems that may be probed using a FCI scanner^5-7. We apply the random matrix theory (RMT) reconstruction^8-10 [Fig.1], to jointly denoise images from a range of field strengths and inversion times to enable precise estimation of $$$T_1$$$ on a stroke patient.

Methods

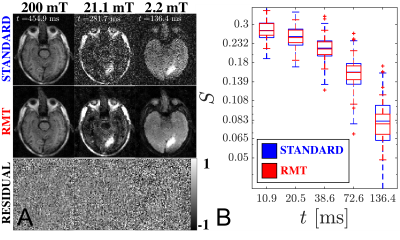
Acquisition
Following informed consent, the brain of a patient with an occipital infarct was imaged on a whole-body FCI scanner⁶ with maximum $$$B_0=200\,\mathrm{mT}$$$ and minimum $$$B_0=50\,\mathrm{\mu T}$$$ [Fig.1]. The acquisition produced 15 images using an inversion recovery spin echo¹¹ initialized with a $$$B_0$$$ pre-polarization pulse at 200 mT that was maintained for 300 ms. Images were acquired at three $$$B_0$$$ field strengths over the following range of evolution times, $$$t$$$: $$$B_0=200\,\mathrm{mT}$$$ with $$$t=[455, 242, 129, 68, 36]\,\mathrm{ms}$$$, $$$B_0=21.1\,\mathrm{mT}$$$ with $$$t=[282, 150, 80, 42, 23]\,ms$$$, $$$B_0=2.2$$$ mT with $$$t=[136, 73, 39, 21, 11]\,\mathrm{ms}$$$. Other imaging parameters include voxel size: $$$2.26 x 2.26 x 10.0 \,\mathrm{mm}^3$$$, partial Fourier$$$ = 6/8$$$, Bandwidth$$$ = 20\,\mathrm{kHz/pixel}$$$, and total acquisition time = 40 minutes.

RMT reconstruction
We employ a segment of the RMT reconstruction procedure to remove noise by leveraging the low-rank nature of the complex-valued images over $$$B_0$$$ and $$$t$$$. Firstly, the Marchenko-Pastur (MP) Distribution¹² was identified to discard noise-only eigenvalues over local 5x5 patches against 15 measurements [3 $$$B_0$$$, 5 $$$t$$$]. The resulting image was used to locally demodulate the phase⁸ of the original image produce a real-valued image, where the imaginary part is discarded. In the following step, MP distribution was identified to discard noise-only eigenvalues over local patches taken from the real-valued image containing 20 similar-intensity voxels across all 15 measurements.

Parameter estimation
$$$T_1$$$ was estimated on magnitude images for each field strength separately, assuming perfect refocusing: $$$S(t)=S_0\cdot(1-e^{-t/T_1})$$$. Parameter estimation of $$$S_0$$$, $$$T_1$$$, and noise level, $$$\sigma$$$, occurred in three steps:
(i) a machine learning polynomial regression approach^13,14 (order = 4) was used to map a simulated signal with Rician noise to $$$S_0$$$, $$$T_1$$$, and $$$\sigma$$$.
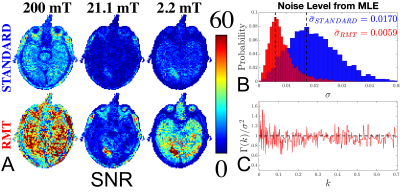
(ii) the result of (i) was used as initialization to max-likelihood estimation (MLE) of $$$S_0$$$, $$$T_1$$$ and $$$\sigma$$$ for the Rician noise distribution¹⁵. The estimated was used to define the signal-to-noise ratio (SNR) [Fig.2].
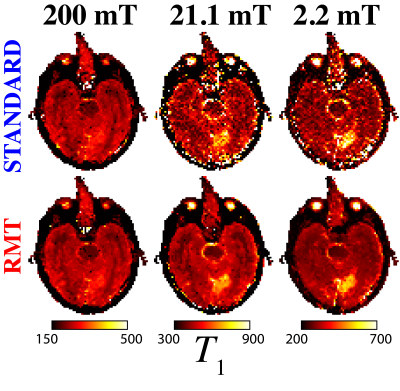
(iii) MLE re-done for $$$\sigma$$$ fixed to its median value across the image from step (ii): Since this acquisition was performed using a single coil, noise should be constant over the image. This 2-parameter MLE yielded maps of $$$T_1$$$ and $$$S_0$$$ [Figs.3-4].

Results & Discussion

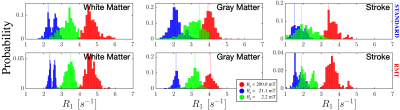
The application of RMT increases SNR and recovers signal from below the noise floor, as evidenced by the re-appearance of gray/white matter boundaries on $$$B_0=21.1\,\mathrm{mT}$$$ in the RMT reconstruction [Fig.1]. Moreover, with relatively few FCI images, the SNR may be improved by ~3x, as demonstrated by the reduction in noise level independently measured with MLE, step (ii) [Fig.2B]. The residuals $$$\epsilon(x)=S_{original}(x)-S_{RMT}(x)$$$ are largely indistinguishable from noise: Their power spectrum, $$$\Gamma(k)=|\epsilon(k)|^2/\mathrm{Area}$$$, is flat, $$$\Gamma(k)/\sigma^2=1$$$. as expected for perfect white noise, Fig.2C. While the standard reconstruction loses gray/white boundaries on maps, these boundaries are clearly visualized on $$$T_1$$$ maps derived from RMT images [Fig.3].

This acquisition is sensitive towards $$$T_1$$$-dispersion, where we observe that the lowest field strength, $$$B_0=2.2$$$ mT, has higher $$$R_1$$$ than the central field strength, $$$B_0=21.1\,\mathrm{mT}$$$, Fig.4. Moreover, there appears to be a bi-modal distribution of $$$R_1$$$ at $$$21.1\,\mathrm{mT}$$$ within the white matter, indicating possible sensitivity to white matter microstructure. This is further evidenced by the remarkable stroke contrast, where the contrast on $$$R_1$$$ increases with decreasing $$$B_0$$$, where the ratio between white matter/stroke ROI reaches 1.63x at $$$2.2\,\mathrm{mT}$$$. This finding suggests that FCI systems may provide an alternative direction for the characterization of ischemic stroke.

The performance of RMT can be further improved with the inclusion of multiple RF channels, and additional images, which would increase the degree of joint-redundancy that is leveraged by RMT. Moreover, the coil-noise dominance at low fields creates the ideal conditions for denoising with random matrix theory. This increase in SNR could then be spent on further accelerating the acquisition and increasing the resolution.

Conclusion

At sufficiently low field, not only are high field concerns for susceptibility and SAR minimized, but also there appears to be an untapped reservoir of uniquely low-field MR contrasts that can be more easily unveiled by using advanced denoising methods. RMT-based methods such as presented here offer excellent capabilities for field-cycling imaging and may be used in other contexts where high redundancy is available in the image stack.

Acknowledgements

The authors thank Santiago Coelho and Els Fieremans for fruitful discussions. This work is supported by the National Institutes of Health (NIH) via R01EB027075 (NIBIB) and R41CA257624 (NCI).

References

1. Campbell-Washburn, A. E. et al. Opportunities in Interventional and Diagnostic Imaging by Using High-Performance Low-Field-Strength MRI. Radiology 293, 384-393, doi:10.1148/radiol.2019190452 (2019).

2 Bloembergen, N., Purcell, E. M. & Pound, R. V. Relaxation Effects in Nuclear Magnetic Resonance Absorption. Physical Review 73, 679-712, doi:10.1103/PhysRev.73.679 (1948).

3 Kiselev, V. G. & Novikov, D. S. Transverse NMR relaxation in biological tissues. Neuroimage 182, 149-168, doi:10.1016/j.neuroimage.2018.06.002 (2018).

4 Ungersma, S. E. et al. Magnetic resonance imaging with T1 dispersion contrast. Magn Reson Med 55, 1362-1371, doi:10.1002/mrm.20910 (2006).

5 Lurie, D. J. et al. Fast field-cycling magnetic resonance imaging. Cr Phys 11, 136-148, doi:10.1016/j.crhy.2010.06.012 (2010).

6 Broche, L. M., Ross, P. J., Davies, G. R., MacLeod, M. J. & Lurie, D. J. A whole-body Fast Field-Cycling scanner for clinical molecular imaging studies. Sci Rep 9, 10402, doi:10.1038/s41598-019-46648-0 (2019).

7 Bodenler, M. et al. Joint multi-field T1 quantification for fast field-cycling MRI. Magn Reson Med 86, 2049-2063, doi:10.1002/mrm.28857 (2021).

8 Lemberskiy, G. et al. Achieving sub-mm clinical diffusion MRI resolution by removing noise during reconstruction using random matrix theory. In Proceedings 27nd Scientific Meeting #0770, International Society for Magnetic Resonance in Medicine, Montreal, Canada, 2019. (2019).

9 Lemberskiy, G. et al. MRI below the noise floor. In Proceedings 28nd Scientific Meeting #3451, International Society for Magnetic Resonance in Medicine, Melbourne, Australia, 2020. (2020).

10 Lemberskiy, G. et al. Feasibility of accelerated diffusion weighted imaging for prostate cancer screening on prototype 0.55T system enabled with random matrix theory. In Proceedings 29nd Scientific Meeting #0742, International Society for Magnetic Resonance in Medicine, Melbourne, Vancouver, 2021. (2021).

11 Ross, P. J., Broche, L. M. & Lurie, D. J. Rapid field-cycling MRI using fast spin-echo. Magn Reson Med 73, 1120-1124, doi:10.1002/mrm.25233 (2015).

12 Veraart, J. et al. Denoising of diffusion MRI using random matrix theory. Neuroimage 142, 394-406, doi:10.1016/j.neuroimage.2016.08.016 (2016).

13 Reisert, M., Kellner, E., Dhital, B., Hennig, J. & Kiselev, V. G. Disentangling micro from mesostructure by diffusion MRI: A Bayesian approach. NeuroImage 147, 964-975, doi:https://doi.org/10.1016/j.neuroimage.2016.09.058 (2017).

14 Coelho, S., Fieremans, E. & Novikov, D. How do we measure tissue parameters, not the prior? In Proceedings 29nd Scientific Meeting #0397, International Society for Magnetic Resonance in Medicine, Melbourne, Vancouver, 2021. (2021).

15 Sijbers, J., den Dekker, A. J., Scheunders, P. & Van Dyck, D. Maximum-likelihood estimation of Rician distribution parameters. IEEE Trans Med Imaging 17, 357-361, doi:10.1109/42.712125 (1998).

Figures

Figure 1: (A) T1-weighted images on standard and RMT reconstructions, as well as their residuals are shown over each field strength. (B) Box plots over all white matter show the signal evolution on B0=2.2 mT.

Figure 2: (A) SNR for each field strength calculated from the noise level estimated from MLE step (ii). (B) Histograms of the noise levels are shown over standard and RMT reconstructions, illustrating ~3x noise reduction for this dataset. (C) Residuals’ power-spectrum Γ(k)/σ² normalized by estimated noise level shows that the residuals are random, i.e., that no anatomy has been removed.

Figure 3: T1 maps for the standard and RMT reconstructions estimated from inversion recovery using MLE of a Rician noise model (step (iii), see text) are shown for each field strength.

Figure 4: Histograms of relaxation rates for white matter, gray matter and stroke ROIs are shown for each field strength for standard and RMT reconstructions. Histograms of R1 become narrower, but less than by 3x, indicating that most of the remaining variations are due to the biological variability of tissue parameters rather than the noise.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

1808

DOI: https://doi.org/10.58530/2022/1808