Introduction

Deep learning (DL) algorithms have achieved state of the art in segmentation of various medical image datasets. Despite promising results, they suffer from over confident predictions which questions their generalisation capabilities. Moreover, producing deterministic outputs hinders DL adoption into clinical routines. Uncertainty estimates for the predictions would permit subsequent revision by clinicians and facilitate the safe deployment of machine learning in the medical diagnosis systems. Fluorinated compounds have significant impact in fields of pharmaceuticals, agrochemicals and household products. However, deposition of these compounds in vulnerable organs has harmful effects to mammals. So a reliable quantification method is essential to estimate concentrations in specific organs (e.g. the brain) to predict treatment and disease outcomes. Available methods to monitor Flourine-19 (¹⁹F) compounds rely on the estimation of the noise level and subtraction of background¹. Since most signals in ¹⁹F magnetic resonance (MR) data are close to detection threshold, background subtraction strongly influences signal sensitivity and most importantly the reliability of the obtained results.This work proposes a 3D Bayesian convolutional neural network which combines recent advances in uncertainty estimation and semantic segmentation to improve the sensitivity of ¹⁹F MRI and accurately quantify ¹⁹F compounds in vivo. Our model does not only increase signal sensitivity in low signal to noise ratio (SNR) ¹⁹F MR data but also assigns uncertainty to each predicted label which enables further analysis in more challenging cases.

Methods

A U-net² and a combination of Binary cross entropy and Dice loss were used for segmentation to address the extreme class imbalance. Segmentation’s performance is evaluated on the test set by Dice score, sensitivity and precision. For the Bayesian model, a specific Markov Chain Monte Carlo (MCMC) method called Stochastic Gradient Hamiltonian Monte Carlo (SGHMC)³ is used. In the Bayesian paradigm we assume the parameters of a model are probabilistic. Then we estimate predictive distribution $$P(y|x,D)$$ by estimating the probability distribution over the parameters, so called posterior $$p(\theta|D)$$ and marginalising over all likely models
$$$P(y|x,D)= \int P(y|x,\theta)~ P(\theta|D)~d\theta\approx \frac{1}{s}\Sigma_{i=1}^{s} p(y|x, \theta_{i}).$$$
The uncertainty in predictions are then quantified by measuring either the variance or the entropy of the predictive distribution⁴. Here we use SGHMC to take 300 samples from the posterior, we measured the uncertainty using entropy computed as:
$$$H(y|x,D) = -\Sigma_{c\in C} p(y=c|x,D) \log p(y=c|x,D)$$$
Where $$c$$ ranges over all classes. We evaluate the quality of estimated uncertainties with respect to their reliability and their benefit to correct the failure predictions in terms of 3 metrics: Calibration⁵: a model is said to be perfectly calibrated if its predictions with confidence p occur with a fraction p of the time. Uncertainty-Error-overlap⁵: is used to determine the overlap between segmentation error and thresholded uncertainty. Corrections⁵: the benefit of uncertainties is assessed by measuring the improvement in Dice score or AUC-ROC when removing uncertain voxels at different thresholds.

Results

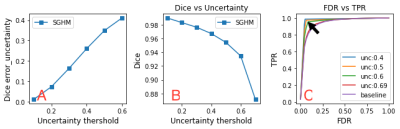
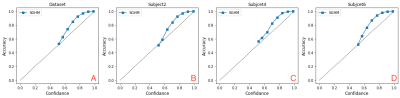
We employed a dataset of 5 ex vivo and 11 in vivo 3D ¹⁹F MRI for training and a dataset of the same size for testing⁶. Each image is of a size of 112x40x40 isotropic (1 mm3) voxels. We split the dataset into 14 training and 2 validation. Segmentation results are summarised in (Table. 1). The input ¹⁹F MRI data (Fig. 1A) were tested and compared to reference (ground truth) ¹⁹F MRI data (Fig. 1B) to predict segmentation masks (Fig. 1C). Uncertainties maps (Fig. 1D) were then used to correct segmentation failures. The highest Dice score between error map and thresholded uncertainty map occurs at 0.6 (Fig. 3D), confirming that the model is most uncertain at voxels that are false positives and certain when it is correct (Fig. 2A). By removing voxels with uncertainty>0.6 (typically ¹⁹F MRI borders) we achieved 93% Dice score without losing too many true positives/negatives (10%/ 1%) which indicates that the model truly assigns the highest uncertainty to the misclassified voxels (Fig. 2B). A ROC curve from plotting true positive rates (TPR) against false detection rates (FDR) at various uncertainty thresholds shows the improvement in TPR/FDR ratios by thresholding uncertain voxels (Fig. 2C). In terms of calibration, calibration diagram (Fig. 3A-D) indicates that the model is perfectly calibrated in both dataset level and subject level.

Discussion

The results show that estimated uncertainties are well-calibrated at both the dataset level and at the subject level (Fig. 3). Moreover, our results indicate that thresholding the most uncertain voxels significantly improve segmentation performance indicating that high uncertainty reflects wrong predictions (Fig. 2). These observations confirm that estimated uncertainties are reliable enough to be used as a mechanism to detect failed segmentations in the absence of the ground truth.

Conclusion

Preliminary work shows that Bayesian based deep learning approaches can provide reliable uncertainty estimations when segmenting ¹⁹F MR images. Such measures are vital as they provide a new option to the ¹⁹F MR scientist to assess predictions of high uncertainty or further analyse uncertain boundaries.

Acknowledgements

No acknowledgement found.