1791
Multi-Scale Evaluation of Uncertainty Quantification Techniques for Deep Learning based MRI Segmentation
Benjamin Lambert1,2, Florence Forbes3, Alan Tucholka2, Senan Doyle2, and Michel Dojat1
1Univ. Grenoble Alpes, Inserm, U1216, Grenoble Institut Neurosciences, GIN, 38000, Grenoble, France, 2Pixyl, Research and Development Laboratory, 38000, Grenoble, France, 3Univ. Grenoble Alpes, Inria, CNRS, Grenoble INP, LJK, 38000, Grenoble, France
1Univ. Grenoble Alpes, Inserm, U1216, Grenoble Institut Neurosciences, GIN, 38000, Grenoble, France, 2Pixyl, Research and Development Laboratory, 38000, Grenoble, France, 3Univ. Grenoble Alpes, Inria, CNRS, Grenoble INP, LJK, 38000, Grenoble, France
Synopsis
Efforts are required to design Deep Learning models that are not only powerful, but also capable of expressing the certainty of their predictions.
We evaluate 3 state-of-the-art techniques for uncertainty quantification : Monte-Carlo Dropout, Deep Ensemble, and Heteroscedastic models. Evaluation is illustrated on a task of automatic segmentation of White-Matter Hyperintensities in T2-weighted FLAIR MRI sequences of Multiple-Sclerosis patients. Analysis is performed at 3 different scales : the voxel, the lesion, and the whole image. Results indicate the superiority of the Heteroscedastic approach, which ranked first in both the uncertainty and segmentation tasks.
Introduction
Deep Learning (DL) techniques have become the gold standard for biomedical image segmentation. Although extensively used, they tend to be considered as black-boxes, preventing their full acceptance in clinical routine. This opacity is partly due to the inability of neural networks to express the uncertainty in their predictions. In recent years, tremendous work has been carried out to alleviate this limitation and develop models that know when they don't know 1.In this work, we propose an in-depth evaluation of 3 state-of-the-art approaches to quantify uncertainty attached to DL predictions : Monte-Carlo Dropout (M1), Deep Ensemble (M2), and Heteroscedastic network (M3). We performed a multi-scale analysis of these techniques by evaluating uncertainty estimates at the voxel, lesion and image levels. We illustrate this comparison on an automatic segmentation task to detect White-Matter Hyperintensities (WMH) from T2-weighted FLAIR MRI sequences of Multiple-Sclerosis (MS) patients.
Methods
Each method (M) provides a lesion probability for each voxel, attached with an uncertainty estimate.M1. Bayesian theory provides a collection of tools to deal with uncertainty, with the drawback of increasing the computational cost. Monte-Carlo Dropout 2 (MC-Dropout) alleviates this problem by considering dropout as a Bayesian approximation. Dropout is used during both training and inference. For a given image, the inference process is repeated T times, resulting in T different predictions. The uncertainty is finally obtained by computing the entropy of the predictive distribution. To test this method, we trained a V-Net 3 convolutional neural network (CNN) with a dropout rate of 20% applied after each convolution, and made 20 inferences per image at test-time.
M2. Deep Ensembles are an alternative approach to quantify uncertainty 4. To form an ensemble, several models are trained sequentially. At inference, each model processes the image and the set of predictions is aggregated to compute the final segmentation. The uncertainty is obtained by computing the variance of the predictive distribution. For the evaluation of this method, we composed an ensemble of 4 different CNN architectures: a V-Net, a U-Net, a Residual U-Net and a V-Net with attention gates.
M3. Heteroscedastic models propose to deal with uncertainty quantification as a learning problem. This type of model predicts the segmentation and its uncertainty together, in a single-step. To achieve this result, the label-flip loss 5 is used to force the model to predict high uncertainties in the areas of unconfident segmentation. To test this technique, we used a Heteroscedastic adaptation of the Vnet CNN.
Evaluation
We used a proprietary brain dataset composed of 238 T2-weighted FLAIR MRI sequences of MS patients, with ground truth segmentations of WMH. The dataset was split into 187 scans for training and 51 for testing. Segmentation masks and uncertainty maps were generated on the test images using each of the three techniques (Figure 1). Evaluation was performed at 3 scales : the voxel (E1), the lesion (E2) and the image (E3).E1. At the voxel-level, we assessed the quality of uncertainty estimates with Area Under Confidence-Classification Characteristic curves (AUCCC) 6 (Figure 2). This metric is agnostic of the model segmentation performance, which is desired for a fair comparison. An AUCCC of 0.5 indicates that the uncertainties of correct and incorrect voxels are confounded, hence meaningless. Alternatively, an AUCCC of 1 indicates that correct voxels are systematically assigned with a lower uncertainty than incorrect voxels.
E2. To convert the voxel uncertainties into lesion-wise uncertainty, we first identified each individual lesion using connected components. Lesion uncertainty was then obtained by computing the mean of its connected components uncertainties. We progressively filtered out lesions according to their uncertainty, and monitored the evolution of the predicted segmentations (number of Lesion True Positives (LTP) and number of Lesion False Positives (LFP)). This stratification approach, inspired from Nair et al. 2020 7, results in a Lesion Stratification curve (Figure 3), where each point corresponds to a couple (LTP, LFP) for a given uncertainty threshold. A quantitative score was finally obtained by computing the Area Under the Lesion Stratification Curve (AULSC).
E3. For each scan, the overall image uncertainty was calculated as the mean of uncertainties of all voxels predicted as lesions 8. We plotted correlation curves between images uncertainties and their Dice scores (segmentation quality) (Figure 4). We used the Pearson correlation coefficient (PCC) between both quantities to assess the quality of image uncertainties, and the Dice scores to estimate segmentation performance.
Results and Conclusion
Results of the multi-scale evaluation are presented in Figure 5, with top-scoring techniques highlighted in green. The Heteroscedastic approach (M3) outperformed competing approaches on 2 of the 3 evaluation scales regarding uncertainty estimates (lanes 1 to 3), as well as for segmentation performance (Dice scores, lane 4). Interestingly, this technique is also the fastest, as uncertainty and segmentation are simultaneously obtained in a single-step, contrary to MC-Dropout (M1) and Deep Ensemble (M2) that require the aggregation of multiple predictions. These multi-steps methods demonstrated lower performances in both the uncertainty and segmentation tasks, while also prolonging inference time (MC-Dropout, M1) or increasing the computational requirements and training times (Deep Ensemble, M2).Acknowledgements
BL, SD and AT are employees of the Pixyl Company. MD and FF serve on Pixyl advisory board.References
1. Abdar, Moloud, et al. A review of uncertainty quantification in deep learning: Techniques, applications and challenges. Information Fusion (2021):243-297.2. Yarin Gal and Zoubin Ghahramani. 2016. Dropout as a Bayesian approximation: representing model uncertainty in deep learning. In Proceedings of the 33rd International Conference on International Conference on Machine Learning - Volume 48 (ICML'16). 1050–1059.
3. Milletari F, Navab N, Ahmadi SA. V-net: Fully convolutional neural networks for volumetric medical image segmentation. In 2016 fourth international conference on 3D vision. IEEE.
4. Lakshminarayanan B, Pritzel A, Blundell C. Simple and scalable predictive uncertainty estimation using deep ensembles. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS'17): 6402-6413.
5. Richard McKinley, Michael Rebsamen, et al. Uncertainty-Driven Refinement of Tumor-Core Segmentation Using 3D-to-2D Networks with Label Uncertainty. BrainLes at MICCAI (1) 2020: 401-411.
6. Huang X, Yang J, Li L, Deng H, Ni B, Xu Y. Evaluating and boosting uncertainty quantification in classification. arXiv preprint arXiv:1909.06030. 2019.
7. Nair T, Precup D, Arnold DL, Arbel T. Exploring uncertainty measures in deep networks for multiple sclerosis lesion detection and segmentation. Medical image analysis. 2020 Jan 1;59:101557.
8. Roy AG, Conjeti S, Navab N, Wachinger C. Inherent brain segmentation quality control from fully convnet monte carlo sampling. In International Conference on Medical Image Computing and Computer-Assisted Intervention 2018 Sep 16 (pp. 664-672). Springer, Cham.
Figures
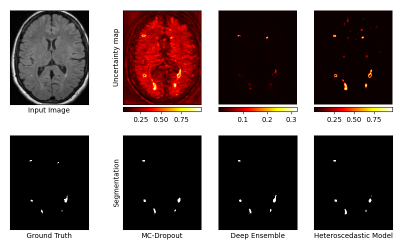
Figure 1 : Example of segmentation masks and uncertainty maps obtained with each technique.
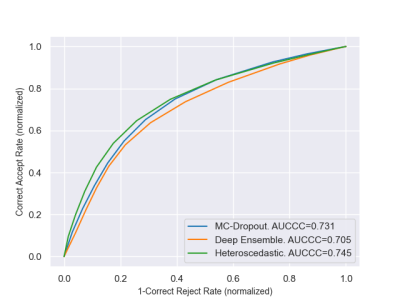
Figure 2 : Confidence-Classification Characteristic curves for voxel-wise evaluation (E1).
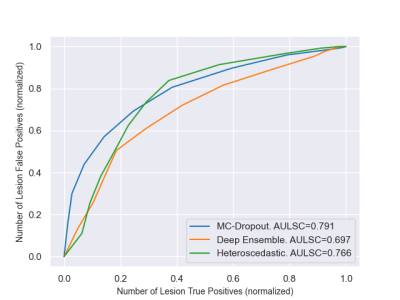
Figure 3 : Lesion Stratification curves for lesion-wise evaluation (E2).
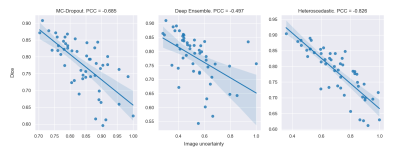
Figure 4 : Correlation curves between image uncertainties and Dice scores for image-wise evaluation (E3).
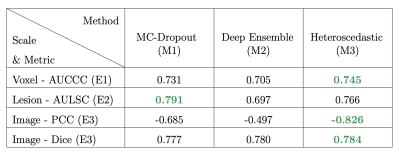
Figure 5 : Results of the multi-scale evaluation. Top performing methods are highlighted in green.
DOI: https://doi.org/10.58530/2022/1791